进化计算（四）——NSGA/NSGA II算法详解

引言

概述

 NSGA系列算法都是基于Pareto支配关系解决多目标优化问题的智能算法。有些问题的Pareto解集很大（可能无界），有效的方法是去找能代表Pareto解集的一系列解。基于Pareto解实现多目标优化问题应该尽量达到三个目标：

• 尽可能接近Pareto解集（理想情况下就是Pareto解集）；
• 均匀分布；
• 能捕捉到Pareto解集的边界，也就是能到达目标函数的极端。

为什么引入NSGA算法解决多目标优化问题

1. 与传统的数学优化（多目标转化为单目标）相比引入NSGA算法解决多目标优化问题的原因见进化计算（三）——多目标优化基本概念。

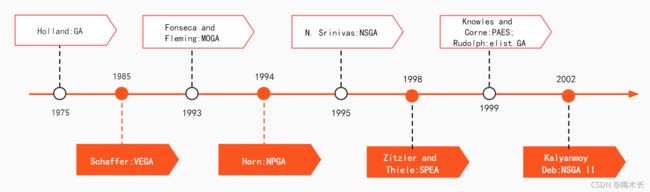
2. 遗传算法是基于种群进行的，所以人们在解决多目标优化问题时很自然的提出可以用遗传算法同时获得一组解，例如Schaffer提出的VEGA（vector evaluated GA）算法。但该算法求解时种群容易很快地收敛在某一目标上特别好但在其他目标上比较差的解。因此，N. Srinivas等人提出了NSGA算法。

3. NSGA算法与基本遗传算法相比仅选择算子不同，在执行选择之前依据个体间的支配关系进行了分层，而交叉算子、变异算子与基本遗传算法没有太大差异。通过非支配分层，可以使好（支配关系高）的个体有更大的机会遗传到下一代。同时，采用适应度共享策略可以使PF上的个体均匀分布，保持了群体多样性，克服了超级个体的过度繁殖，防止了早熟收敛。

 遗传算法向NSGA算法过渡的过程中，引入了非支配排序、虚拟适应度、共享小生境等技术（本文不对这些技术进行具体讲解，仅在下文中用作与NSGA II对比时简单阐述关键技术，更多内容可参考该篇博客）。

为什么引入NSGA II算法

 主要有如下三个原因(NSGA的局限性)：

• 非支配排序的计算量大：计算复杂度为$O(M{N}^3)$，$M$为目标函数的数量（优化目标个数），$N$为种群规模（种群内的个体数）；【具体计算见下文】
• 缺乏精英策略：精英策略可以显著提升GA算法的执行性能，同时减少已知优解被丢失的情况；
• NSGA需要特殊指定的共享参数${\sigma }_{share}$：NSGA算法中通过共享机制确保种群多样性，共享机制过于依赖共享参数。

 NSGA过渡到NSGA II的过程中，引入了快速非支配排序、拥挤度和拥挤距离、精英策略等概念。

简单介绍一下早期使用GA解决多目标优化的方法

发展时间节点一览

不使用Pareto支配关系

1. 加权和方法

• MBGA：每个个体在计算目标函数值时，各目标函数的权重 w={ w1, w2, … , wk } 都不同；
• RWGA：w={ w1, w2,…, wk } 是随机的。

 优点——容易实现；缺点：如果Pareto解集是非凸的，不是所有的Pareto解都能被搜到。

2. 并列选择法

  VEGA：采用成比例选择机制，针对每个子目标函数产生对应的一个子群体。即：如果多目标问题具有$k$个子目标函数,需随机产生$k$个子群体,每个子群体的规模为$N/k$ ,其中$N$为整个群体规模。各子目标函数在其相应的子群体中独立进行评价和选择,之后组成一个新的群体进行交叉和变异操作,如此循环执行分割、并列、评价、选择、合并过程,最终求出问题的非劣解。

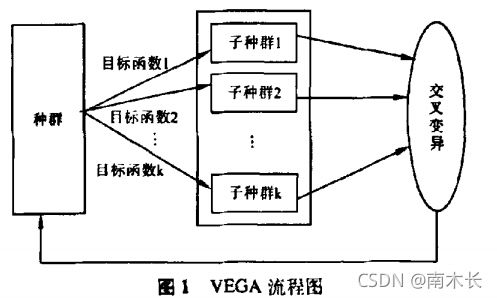
【参考：基于向量评估遗传算法的多目标优化效果评价及程序测试】

使用Pareto支配关系

1. 利用Pareto支配关系——MOGA、NPGA、NSGA
    1)基于非支配排序为种群个体分配适应度值；
    2)在同一非支配层上保持种群多样性。
   

2. 进一步引进精英策略——SPEA、PAES、elist GA
   SPEA：
    (1)精英策略：在每一代保留一个外部种群用于存储从初始种群至今发现的所有非支配解。每一代首先构建一个由当前种群和外部种群组成的组合种群，然后基于组合种群中各个非支配解所支配的解的数量为其分配一个适应度值，对于其他被支配的解，为其分配的 适应度值应小于非支配解中分配的最小的适应度值。
    (2)保存种群多样性：使用一种确定性聚类的方法确保非支配解之间的多样性。确定性算法的概念
   
   PAES:使用类似 “(1+1)-ES”的single-parent single-offspring EA 方法
    在PAES算法中，不使用真实的参数产生子代，而是将其转换为二进制字符串后采用按位变异的方法产生子代。核心迭代遗传方法如下（针对一个父代和一个子代）：
    (1)子代支配父代，子代作为下一个父代继续迭代；
    (2)父代支配子代，忽略该子代并生成一个新子代后—>(1)；
    (3)子代与父代互不支配，将子代和父代与迄今为止存档中已有的最优解进行比较：
     ①首先将子代与存档中的解进行对比：若子代支配存档中任一解，该子代作为新父代同时将被支配解从存档中剔除；若存档中无子代可支配解，则—>②；
     ②同时将父代和子代与存档中的近距离解作对比：如果子代位于存档成员所在目标空间中的最小拥挤区域，该子代作为新父代并将该子代复制到存档中。
   
   elist GA[未经仿真]:基于子代和父代个体间系统的比较：将子代中的非支配解与父代中的非支配解比较并形成一个整体的非支配解集作为下一次迭代的父辈。如果该解集大小不满足种群规模大小，则将子代中其他的个体也纳入解集中。
   
   

NSGA & NSGA II

 NSGA II核心算法主要由两部分构成：快速非支配排序、拥挤比较算子，文章中选用的选择策略为tournament selection(锦标赛选择法)，其他重组、变异算子等步骤与基本遗传算法没有太大的差异。参考：遗传算法解决单目标优化的MATLAB编程。

Fast nondominated sorting approach

NSGA——原始非支配排序

 排序前，随机生成N个决策向量作为初始种群中的N个个体。

1. 第一层非支配前沿（nondominated front）的确定：每个solution都要和种群中的其他solution进行支配关系比较。具体复杂度计算如下：
   (1)每个solution都要与其他N-1个解分别比较M次—>$O(MN)$
   (2) 遍历所有的solution进行支配关系比较，总复杂度就变成了$O(M{N}^2)$
   至此，第一层非支配前沿完成查找；
2. 第二层非支配前沿：第一层上的solution可以暂时不列入考虑范围，对种群中的其他个体按照支配与非支配关系分层。最坏情况下，N个个体都位于第二层或者更高层，确定第二层的复杂度也可以达到$O(M{N}^2)$；
   … …

  直到N个个体均完成分层，非支配排序算法结束。

• Worst case：最坏情况下，N个个体位于N个前沿（每层仅有一个个体），总复杂度可以达到$O(M{N}^3)$。

NSGA II——快速非支配排序（$n_i$、$S_i$）

 在快速非支配排序算法中，每个solution都会被分配两个参数：$n_i$、$S_i$。其中，$n_i$表示支配第$i$个解的解的个数，$S_i$表示第$i$个解所支配的解的个数。

1. 首先，我们可以通过计算遍历获取各个solution的$n_i$及$S_i$，该步的计算复杂度为$O(M{N}^2)$。【普通非支配排序的第一步就可以获取该步的结果】
2. 易判断,第一个非支配层上的解满足$n_i=0$，我们可以将这些解存进集合$F_i$中。对于$F_i$集中$n_i=0$的解，将其所支配个体（$S$集合中的个体）的$n_i-1$。此时，新出现的$n_i=0$的个体就可以作为第二个非支配层上的解。我们将这些新出现的$n_i=0$的个体放入另一个独立集合Q中。
3. 针对集合Q中的个体，重复2中的步骤，即可找到第三层非支配层。
4. 重复上述步骤，就可以找到所有的非支配层。
5. 在完成每层解的划分时会给该层的解分配一个等级rank。

 易知，在二层及以上层的个体其$n_i$最大为N-1（该解被其他N-1个解支配）。因此，这些个体在$n_i$变为0之前（即完成分层之前）最多会被访问N-1次。这样的解最多有N-1个，因此，步骤234遍历时最大的计算复杂度可以达到$O(N^2)$。因此，快速非支配算法的计算复杂度为$O(M{N}^2)$。


 快速非支配排序的伪代码如下图所示：

Diversity Preservation

 该部分的算法主要是为了保障种群多样性，使所求解集尽可能地均匀分布。

NSGA——sharing function approach（${\sigma }_{share}$）

 NSGA采用共享函数保障种群多样性，关键是选择一个合适的共享参数。共享参数${\sigma }_{share}$决定虚拟适应度被共享的程度。实际计算中，该参数代表了种群中任意两个共享虚拟适应度的个体之间的最大欧几里得距离。该方法存在如下两个问题：

1. 该方法的性能过度依赖共享参数${\sigma }_{share}$；（通常为用户自己设定）
2. 需要计算所有个体之间的欧几里得距离并进行比较，复杂度为$O(N^2)$。

NSGA II —— crowded-comparison approach

 该方法的最大优势在于无需设定任何参数，同时计算复杂度也有了一定程度的优化。拥挤度和拥挤度比较算子是该部分算法的两个关键概念。

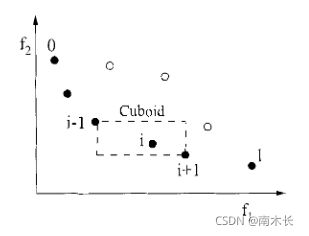
1. 拥挤度的确定：种群中的每个个体都设定一个拥挤度参数：$i_{distance}$。如果解$i$属于非支配层$I$（Nondominated Front）。在非支配层$I$上，解$i$拥挤度/拥挤距离的计算方法如下：针对每个目标函数，找出与该解函数值相邻的两个解并计算这两个解之间的函数差值。当前解的拥挤距离就是所有目标函数获得的相邻解函数差值之和。（每个非支配层的边界的个体拥挤度直接设为无穷大）。

  抽象理解：第i个解的拥挤距离就是其所在非支配前沿上相邻两点构成的长方形cuboid周长。（以同一支配层的最近邻点作为顶点的长方形）

  伪代码：

2. 拥挤度比较算子：由1中抽象理解图片可看出，拥挤距离越小就代表该个体周围越拥挤。为了保障解分布的均匀性，我们定义了拥挤度比较算子$\prec n$。
   

  经过前边的计算，种群中的每个个体都具备了非支配等级$i_{rank}$和拥挤度距离$i_{distance}$这两个属性。基于这两个属性，定义以下偏序关系：
$$\begin{gathered} i{\prec }_{n}j \\ if(i_{rank}<j_{rank}or{i}_{rank}=j_{rank}\wedge i_{distance}>j_{distance}) \end{gathered}$$
即：如果两个解具有不同的rank，我们偏向于低rank的解；如果两个解具有相同的rank，我们偏向于大distance的解。

Main Loop

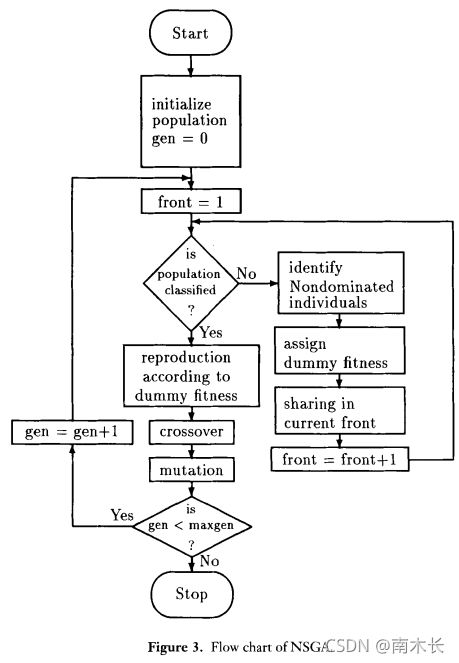
NSGA

 算法流程图如下：
  dummy：虚拟；
  reproduction：复制。

NSGA II

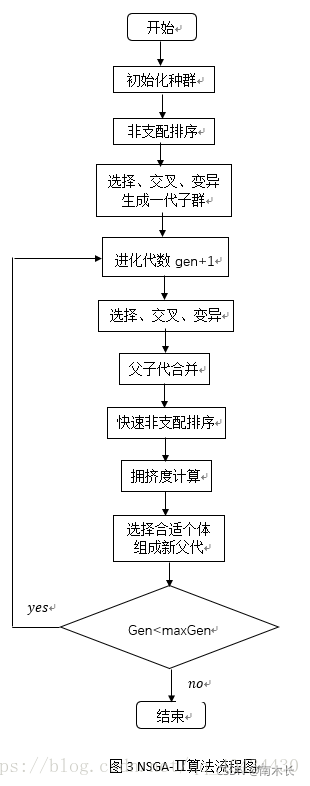
 算法流程如下：

1. 生成初始种群$P_0$，并完成快速非支配排序。此时，每一个解都被分配了一个等于其rank的虚拟度。即$fitnessvalue=i_{rank}$。
2. 在初始种群中使用锦标赛选择机制、复制、变异算子生成子代种群$Q_0$。
3. 初始种群与子代种群$Q_0$合并后构成规模为$2N$的种群，在$2N$的种群上完成快速非支配排序、拥挤度计算，根据拥挤度比较算子（即偏序关系$\prec n$）从第一层开始进行选择直到选够N个可以作为新父代种群的个体。【精英策略】
   
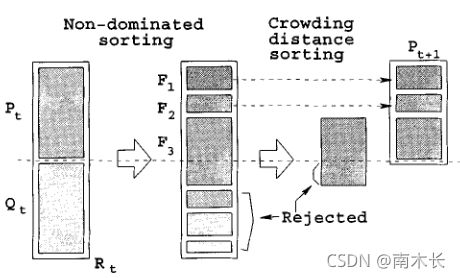
4. 对新父代种群进行选择、交叉、变异，生成子代种群，合并子代和父代种群后进入下一轮循环。直至迭代次数达到预先设定的最大值。
   

  伪代码：

参考链接及文献

• 博客1：Multi-objective optimization using genetic algorithms: A tutorial 阅读笔记;
• 博客2：非支配排序遗传算法 —NSGA、NSGA-II;
• 博客3：多目标遗传算法NSGA;
• 博客4：多目标优化算法（一）NSGA-Ⅱ（NSGA2）;
• 文献1：基于向量评估遗传算法的多目标优化效果评价及程序测试；
• 文献2：Muiltiobjective Optimization Using Nondominated Sorting in Genetic Algorithms；
• 文献3：A fast and elitist multiobjective genetic algorithm NSGA-II；