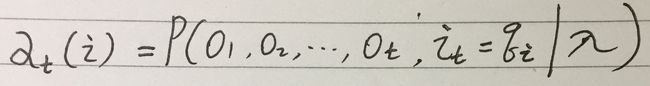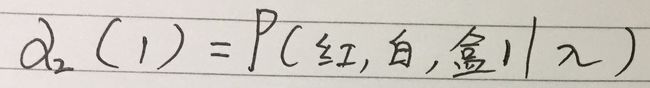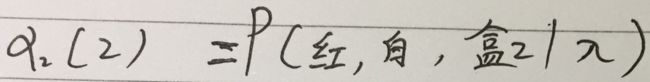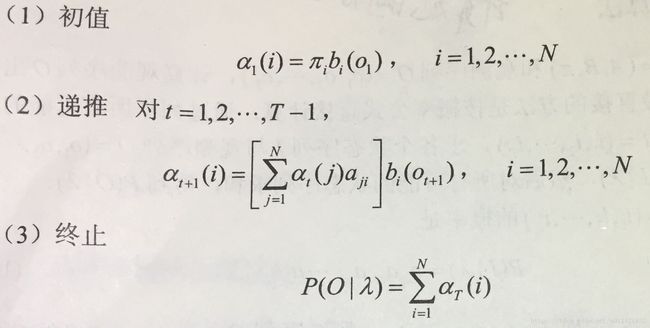【机器学习】【隐马尔可夫模型-2】前向算法：算法详解+示例讲解+Python实现

0.前排提示

csdn有些数学公式编辑不出来，所以本博用容易书写的表达式来表示专业数学公式，如：

 （1）  在本博客中用α(i)来表示

  （2）在本博客中用[i=1, N]∑来表示

注：这是为了表示一些无法编辑出来的数学公式而本博自己想出来的表示方法，不是专业使用，在离开此博客时请忘记他们~~

1.隐马尔可夫模型简介

    隐马尔可夫模型的详细讲解，请详见：【机器学习】【隐马尔可夫模型-1】基本概念+观测序列的生成算法+示例讲解

2.前向算法简介

2.1前向算法的需求背景

首先简要介绍下前向算法的需求背景。

隐马尔可夫模型有3个问题：概率计算问题，学习问题，预测问题。前向算法就是为了解决概率计算问题的。

概率计算问题描述如下：

已知一个隐马尔可夫模型λ=（A，B，λ），已知一个观测序列O=（o1, o2,……，oT）

问题：请计算在模型λ下观测序列O出现的概率P(O|λ)

HMM的这个概率计算问题有前向算法和后向算法，本博客介绍前向算法，后向算法在后面博客介绍。

到此前向算法的需求背景讲解完了，下面开始详解前向算法。

2.2前向概率

已知隐马尔可夫模型λ=（A, B, π），定义到时刻t(t

用博主自己定义的书写表达式就是：

α(i) = P(o<1>，o<2>，……，o，i = q | λ)

看似比较难理解，举个例子：

在时刻t=2，我们得到观测序列（红， 白），且状态为盒1的概率，就是一个前向概率，记作：

在时刻t=2，观测序列为（红，白），状态为盒2的概率，就是一个前向概率，记作：

2.3观测序列概率的前向算法

可以递推得前向概率以及观测序列概率P(O|λ)

输入：隐马尔卡夫模型λ=(A, B, π)，观测序列O

输出：观测序列概率P(O | λ)

核心是通过模型λ=(A, B, π)以及α(i)来递推得到后一个前向概率α(i).直到递推得到α(i)

上面前向算法的步骤比较容易理解，如果看不懂，可以借助下面的示例来理解就变得很容易啦。

话不多说，直接上例子。

3.观测序列概率的前向算法示例

3.1模型λ

从前面介绍的内容可知，模型λ由三个对象确定表示：λ=(A, B, π)=(状态转移概率分布，观测概率分布，初始状态概率分布)

考虑盒子和球模型λ=(A, B, π)，此模型相关信息我们假设给定为：

1）状态集合Q={盒子1， 盒子2， 盒子3}，N=3

2）观测集合V={红，白}，M=2

3）状态转移概率分布 A = [0.5，0.2，0.3

                                               0.3，0.5，0.2

                                               0.2，0.3，0.5]

4）观测概率分布B=[0.5，0.5

                                    0.4，0.6

                                    0.7，0.3]

5）初始状态概率分布π=[0.2

                                            0.4

                                            0.4]

3.2问题

请用前向算法求观测序列概率：已知观测序列O=(红，白，红)，T=3，请用前向算法求P(O|λ)

3.3简单介绍

在进行求解之前，做下简单介绍：

π表示状态为i的初始概率，i是模型中状态集合I={1， 2，3}中的元素状态值，则i可以取1、2或者3，举例：

    π<1>表示初始状态为盒1的概率，即π<1>=0.2

    π<2>表示初始状态为盒1的概率，即π<2>=0.4

    π<3>表示初始状态和盒3的概率，即π<3>=0.4

b表示状态为盒i时观测概率分布，平民说法就是从盒i取出球，球颜色的概率分布，举例：

    b<1>表示状态为盒1时观测概率分布，即b<1> = [0.5，0.5] 

     b<2>表示状态为盒2时观测概率分布，即b<2> = [0.4，0.6]

     b<3>表示状态为盒3时观测概率分布，即b<3>=[0.7，0.3]

b(红)表示状态为盒i时观测为红的概率，平民说法就是从盒i中取出红球的概率~，

b(白)表示状态为盒i时观测为白的概率，平民说法就是从盒i中取出白球的概率~，举例：

    b<1>(红)=0.5，b<1>(白)=0.5

    b<2>(红)=0.4，b<2>(白)=0.6

    b<3>(红)=0.7，b<3>(白)=0.3

o表示观测序列O=(o<1>, o<2>，……，o)中的第i个观测，举例：

示例中给出了观测序列O=(红，白，红)，则o<1>=红，o<2>=白，o<3>=红

a表示从状态i转移到状态j的概率，举例：

示例中给出了状态转移概率分布 A = [0.5，0.2，0.3                 #a<11>=0.5，a<12>=0.2，a<13>=0.3

                                                                 0.3，0.5，0.2                #a<21>=0.3，a<22>=0.5，a<23>=0.2

                                                                 0.2，0.3，0.5]               #a<31>=0.2，a<32>=0.3，a<33>=0.5

a<11>表示当前盒子1取球后，下次取球的盒子是盒1的概率，a<13>表示当前盒子1取球后，下次取球的盒子是盒3的概率

3.4前向算法求解观测序列的概率

下面开始前向算法的求解过程：

Step1：计算初值

下面用初始状态概率分布π和观测概率分布B计算时刻1的观测序列的概率，通用公式：α(i) = π*b(o)：

α<1>(1) = α<时刻1>(状态1) = π<状态1>*b<状态1>(o<时刻1>) = π<盒1>*b<盒1>(红球) = 0.2 * 0.5 = 0.10

α<1>(2) = α<时刻1>(状态2) = π<状态2>*b<状态2>(o<时刻1>) = π<盒2>*b<盒2>(红球) = 0.4 * 0.4 = 0.16

α<1>(3) = α<时刻1>(状态3) = π<状态3>*b<状态3>(o<时刻1>) = π<盒3>*b<盒3>(红球) = 0.4 * 0.7 = 0.28

Step2：递推计算

下面用时刻1的观测序列的概率 递推计算 时刻2的观测序列的概率：

α<2>(1) = （[i=1, 3]∑α<1>(i)*a）*b<1>(o<2>) 
=[α<1>(1)*a<11> + α<1>(2)*a<21> + α<1>(3)*a<31>] * b<1>(o<2>)

=[α<时刻1>(盒1)*a<11> + α<时刻1>(盒2)*a<21> + α<时刻1>(盒3)*a<31>] * b<盒1>(白)

=[0.10*0.5 + 0.16*0.3 + 0.28*0.2] * 0.5 = 0.154 * 0.5 = 0.077，即α<时刻2>(盒1)=0.077

α<2>(2) =  （[i=1, 3]∑α<1>(i)*a）*b<2>(o<2>)

=[α<1>(1)*a<12> + α<1>(2)*a<22> + α<1>(3)*a<32>] * b<2>(o<2>)

=[α<时刻1>(盒1)*a<12> + α<时刻1>(盒2)*a<22> + α<时刻1>(盒3)*a<32>] * b<盒2>(白球)

=[0.10*0.2 + 0.16*0.5 + 0.28 *0.3] * 0.6 = 0.184 * 0.6 = 0.1104，即α<时刻2>(盒2)=0.1104

α<2>(3) = （[i=1, 3]∑α<1>(i)*a）* b<3>(o<2>)

=[α<1>(1)*a<13> + α<1>(2)*a<23> + α<1>(3)*a<33>] * b<3>(o<2>)

=[α<时刻1>(盒1)*a<13> + α<时刻1>(盒2)*a<23> + α<时刻1>*a<33>] * b<盒3>(白球)

=[0.10*0.3 + 0.16*0.2 + 0.28*0.5] * 0.3 = 0.202 * 0.3 = 0.0606，即α<时刻2>(盒3)=0.0606

得：α<时刻2>(盒1) = 0.077，α<时刻2>(盒2)=0.1104，α<时刻2>(盒3)=0.0606

下面用时刻2的观测序列的概率 递推计算 时刻3的观测序列的概率：

α<3>(1) = （[i=1, 3]∑α<2>(i)*a）* b<1>(o<3>)

=[α<2>(1)*a<11> + α<2>(2)*a<21> + α<2>(3)*a<31>] * b<1>(o<3>)

=[α<时刻2>(盒1)*a<11> + α<时刻2>(盒2)*a<21> + α<时刻2>(盒3)*a<31>] * b<盒1>(红球)

=[0.077*0.5 + 0.1104*0.3 + 0.0606*0.2] * 0.5 = 0.08374 * 0.5 = 0.04187，即α<时刻3>(盒1) = 0.04187

α<3>(2) = （[i=1, 3]∑α<2>(i)*a）* b<2>(o<3>)

=[α<2>(1)*a<12> + α<2>(2)*a<22> + α<2>(3)*a<32>] * b<2>(o<3>)

=[α<时刻2>(盒1)*a<12> + α<时刻2>(盒2)*a<22> + α<时刻2>(盒3)*a<32>] * b<盒2>(红球)

=[0.077*0.2 + 0.1104*0.5 + 0.0606*0.3] * 0.4 = 0.08878 * 0.4 = 0.035512，即α<时刻3>(盒2) = 0.035512

α<3>(3) = （[i=1, 3]∑α<2>(i)*a） * b<3>(o<3>)

=[α<2>(1)*a<13> + α<2>(2)*a<23> + α<2>(3)*a<33>] * b<3>(o<3>)

=[α<时刻2>(盒1)*a<13> + α<时刻2>(盒2)*a<23> + α<时刻2>(盒3)*a<33>] * b<盒3>(红球)

=[0.077*0.3 + 0.1104*0.2 + 0.0606*0.5] * 0.7 = 0.07547999999999999 * 0.7 = 0.05284，即α<时刻3>(盒3) = 0.05284

得：α<时刻3>(盒1) = 0.04187，α<时刻3>(盒2) = 0.035512，α<时刻3>(盒3) = 0.05284

Step3：终止

P(O|λ) = [i=1, 3]∑α<3>(i)

=α<3>(1) + α<3>(2) + α<3>(3)

=α<时刻3>(盒1) + α<时刻3>(盒2) + α<时刻3>(盒3) = 0.04187 + 0.035512 + 0.05284 = 0.130222

到此已经求得观测序列O(红，白，红)，T=3的概率 P(O|λ)=0.13022

4.Python实现前向算法

4.1前向算法的python代码

人肉码完，代码如下：

注：只使用numpy.multiply()完成了所有前向概率的计算，包括前向概率的初始值以及递推计算每个时刻t观测序列的前向概率

# -*- coding: utf-8 -*-
"""
@author: 蔚蓝的天空tom
Aim:实现HMM的前向算法(Forward Algorithm)
Aim:已知一个马尔可夫模型λ=(A, B, π)，给定一个观测序列O，请用前向算法求此观测序列出现的概率
"""
import numpy as np
class CHMMForward(object):
    '''隐马尔可夫模型求观测序列的前向算法
    '''
    def __init__(self, A, B, pai):
        '''
        :param A:状态转移概率分布
        :param B:观察概率分布
        :param pai:初始状态概率分布
        '''
        self.A = np.array(A)      #状态转移概率分布
        self.B = B      #观测概率分布
        self.pai = pai  #初始状态概率分布
    def forward(self, A, B, pai, O):
        N,T = np.shape(A)[0], np.shape(O)[0] #隐马尔可夫模型的状态个数N，观测序列的时刻个数T
        print('HMM的状态个数N=%d'%N, '观测序列的时刻总数T=%d'%T)
        
        alpha = np.zeros((T, N)) #保存每个时刻每个状体的观测序列出现的概率
        #[[ 0.1       0.16      0.28    ]
        # [ 0.077     0.1104    0.0606  ]
        # [ 0.04187   0.035512  0.052836]]
        for t in range(T): #[T-1, T-2, ..., 0]
            if 0 == t: #计算初值
                alpha[t] = np.multiply(pai.T, B[:, O[t]])
                print('alpha_t0:', alpha[t])
            else: #递推计算时刻t每个状态的观测序列出现的概率
                for i in range(N):
                    alpha_t_i = np.multiply(alpha[t-1], A[:, i])*B[i, O[t]]
                    alpha[t,i] = sum(alpha_t_i) #时刻t状态i所有观测序列出现的概率之和
            print('\n时刻%d'%t,'每个状态的观测序列的概率:', alpha[t])
            print('update alpha:\n', alpha)
        #时刻T所有状态的观测序列概率之和，就是目标观测序列出现的概率
        return sum(alpha[-1])
 
    def GetProb(self, O):
        '''
        :param O:观测序列，求此观测序列出现的概率
        '''
        return self.forward(self.A, self.B, self.pai, O)
 
def CHMMForward_manual():
    #隐马尔可夫模型λ=(A, B, pai)
    #A是状态转移概率分布，状态集合Q的大小N=np.shape(A)[0]
    #从下给定A可知：Q={盒1, 盒2, 盒3}, N=3
    A = np.array([[0.5, 0.2, 0.3],
                  [0.3, 0.5, 0.2],
                  [0.2, 0.3, 0.5]])
    #B是观测概率分布，观测集合V的大小T=np.shape(B)[1]
    #从下面给定的B可知：V={红，白}，T=2
    B = np.array([[0.5, 0.5],
                  [0.4, 0.6],
                  [0.7, 0.3]])
    #pai是初始状态概率分布，初始状态个数=np.shape(pai)[0]
    pai = np.array([[0.2],
                    [0.4],
                    [0.4]])
    hmm = CHMMForward(A, B, pai)
    
    O = [0, 1, 0] #0表示红色，1表示白，就是(红，白，红)观测序列
    prob = hmm.GetProb(O)
    print('\n通过HMM的前向算法计算得到：观测序列',O,'出现的概率为:', prob)

if __name__=='__main__':
    CHMMForward_manual()

4.2算法运行结果

runfile('C:/Users/tom/HMM_Forward_Algorithm.py', wdir='C:/Users/tom')
隐马尔可夫模型的状态个数N= 3
观测序列的总长度T= 3

时刻0 每个状态的观测序列的概率alpha_0: [[ 0.1   0.16  0.28]]
alpha:
 [[ 0.1   0.16  0.28]]

时刻1 每个状态的观测序列的概率alpha_1: [[ 0.077   0.1104  0.0606]]
alpha:
 [[ 0.1     0.16    0.28  ]
 [ 0.077   0.1104  0.0606]]

时刻2 每个状态的观测序列的概率alpha_2: [[ 0.04187   0.035512  0.052836]]
alpha:
 [[ 0.1       0.16      0.28    ]
 [ 0.077     0.1104    0.0606  ]
 [ 0.04187   0.035512  0.052836]]

通过HMM的前向算法计算得到：观测序列 [0, 1, 0] 出现的概率为: 0.130218

5.精简的前向算法代码

# -*- coding: utf-8 -*-
"""
@author: 蔚蓝的天空tom
Aim:实现HMM的前向算法(Forward Algorithm)
Aim:已知一个马尔可夫模型λ=(A, B, π)，给定一个观测序列O，请用前向算法求此观测序列出现的概率
"""

import numpy as np

class CHMMForward(object):
    '''
    隐马尔可夫模型求观测序列的前向算法
    '''
    def __init__(self):
        pass

    def Forward(self, A, B, pai, O):
        '''
        :param A:状态转移概率分布
        :param B:观察概率分布
        :param pai:初始状态概率分布
        :param O:观测序列，求此观测序列出现的概率
        :return 观测序列O出现的概率
        '''
        N,T = np.shape(A)[0], np.shape(O)[0] #隐马尔可夫模型的状态个数N，观测序列的时刻个数T
        alpha = np.zeros((T,N)) #保存每个时刻每个状态的观测序列出现的前向概率
        for t in range(T):
            if 0 == t:#计算初值
                alpha[t] = np.multiply(pai.T, B[:,O[t]])
            else:#递推计算时刻t每个状态的观测序列出现的概率
                for i in range(N):
                    alpha_t_i = np.multiply(alpha[t-1], A[:,i])*B[i, O[t]]
                    alpha[t,i] = sum(alpha_t_i)
        print('alpha:\n', alpha)
        return sum(alpha[t])

def CHMMForward_manual():
    #隐马尔可夫模型λ=(A, B, pai)
    #A是状态转移概率分布，状态集合Q的大小N=np.shape(A)[0]
    #从下给定A可知：Q={盒1, 盒2, 盒3}, N=3
    A = np.array([[0.5, 0.2, 0.3],
                  [0.3, 0.5, 0.2],
                  [0.2, 0.3, 0.5]])
    #B是观测概率分布，观测集合V的大小T=np.shape(B)[1]
    #从下面给定的B可知：V={红，白}，T=2
    B = np.array([[0.5, 0.5],
                  [0.4, 0.6],
                  [0.7, 0.3]])
    #pai是初始状态概率分布，初始状态个数=np.shape(pai)[0]
    pai = np.array([[0.2],
                    [0.4],
                    [0.4]])
    hmm = CHMMForward()
    
    O = [0, 1, 0] #0表示红色，1表示白，就是(红，白，红)观测序列
    prob = hmm.Forward(A, B, pai, O)
    print('\n通过HMM的前向算法计算得到：观测序列',O,'出现的概率为:', prob)

if __name__=='__main__':
    CHMMForward_manual()

5.2运行结果

alpha:
 [[ 0.1       0.16      0.28    ]
 [ 0.077     0.1104    0.0606  ]
 [ 0.04187   0.035512  0.052836]]

通过HMM的前向算法计算得到：观测序列 [0, 1, 0] 出现的概率为: 0.130218

可知：算法运行结果和我们上面数学计算出来的结果一样~，可以验证算法程序ok~

如果还不懂已知隐马尔可夫模型λ，用前向算法求解给定观测序列O的概率，请抛砖过来吧

(end)