一篇菜鸡的笔记——Dijkstra算法详解

最近上课学到了图的最短路径问题，感触颇多，尤其对于Dijkstra算法有了一定的理解（能想出来真的nb），其实就是贪心算法的一种实现，一步步，一层层，贪眼前，得最优。

Dijkstra算法简介

Dijkstra算法是荷兰计算机科学家–艾兹格·W·迪科斯彻(小本本里又多了一个dalao)提出来的，主要是用于解决单源带权最短路径的问题，是
贪心算法 的一种应用。

扩展资料：

艾兹格·W·迪科斯彻 （Edsger Wybe Dijkstra，1930年5月11日~2002年8月6日）荷兰人。 计算机科学家，毕业就职于荷兰Leiden大学，早年钻研物理及数学，而后转为计算学。曾在1972年获得过素有计算机科学界的诺贝尔奖之称的图灵奖，之后，他还获得过1974年 AFIPS Harry Goode Memorial Award、1989年ACM SIGCSE计算机科学教育教学杰出贡献奖、以及2002年ACM PODC最具影响力论文奖。
资料来源：百度百科

具体实现：单源最短路

假设现在给你一个带权的有向连通图，图有5个顶点，8条边，让你计算从顶点1开始，到其他所有点的最短路径。

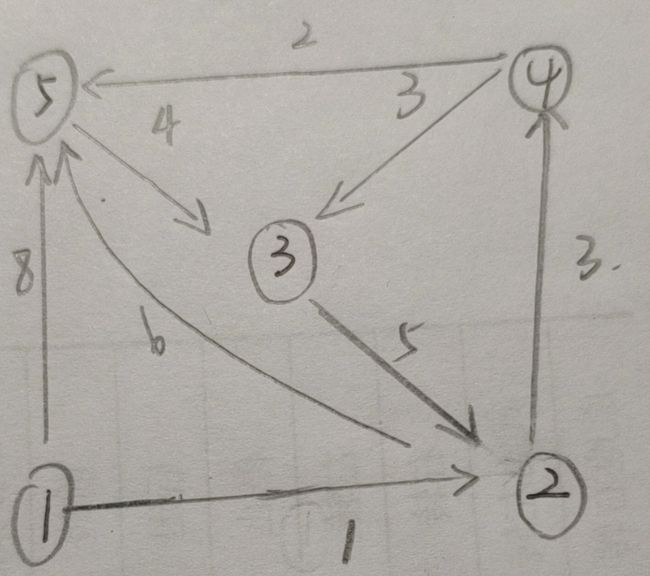
我们可以让所有的点到源点的最短路径都用一个dist数组存放。如果是无权图，那问题就很简单，直接从源点BFS，来生成dist,但是对于带权图的最短路径就不可行，因为要考虑到路径带权，边数多的路径可能短。所以Dijkstra算法就孕育而生了。

采用Dijkstra算法意在一步步确定每一个结点的最短路径，而每一步都是“贪”最优。所以在这里我们用了两个集合S和S’，一个是dist已经确定了的所有点的集合，另一个是还未最终确定的点的集合。开始的时候S是空的，所有的点都存放在S‘中，并且把所有点的dist都设置为默认的 ∞ ，接下来我们让 dist[ 1 ]=0 (显而易见,自己到自己肯定是0，除非你人格分裂，( ╯□╰ ))，既然 1 的dist现在确定了，那么就可以把 1 放到S集合中去。如下图：

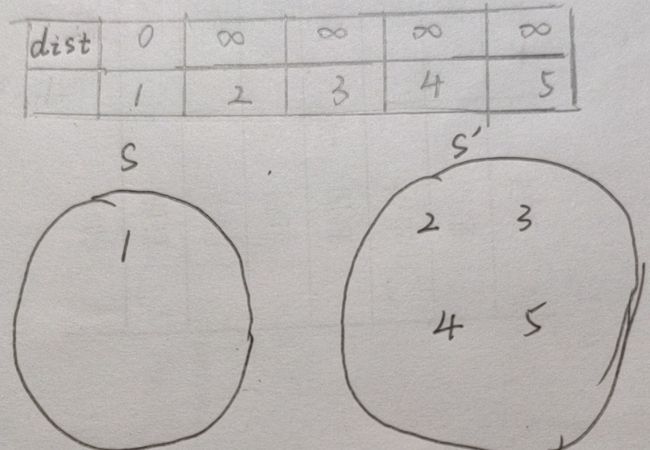
我们可以一眼就知道，1和2、5是有直接边的，所以当前dist[ 2 ]=1,dist[ 5 ]=8 这是毫无疑问的。但是实际上，我们的思维不是这样的！！
现在的状况是，1这个点刚刚被我们放到S集合中去，dist[1]=0是前一秒才被我们确定下来的，所以我们考虑的应该是，dist[ 1 ]的确定，会给其他的未确定的点的dist造成什么影响？？？而现在能被1影响到的是不是就是它的两个邻接点 2 和 5 呢？所以我们的思路应该是dist[ 1 ]的确定可能会影响到dist[ 2 ]、dist[ 5 ]的值的更新，恰好当前这两个值都是∞ ，因此，dist[ 2 ]、dist[ 5 ]都被更新为dist[ 1 ] + 点 ”1“ 到他们的路径长度，结果就是1和8.现在dist数组状态如下：

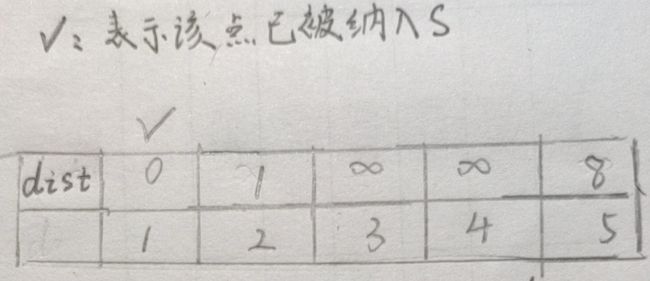
现在 1 是唯一一个被纳入S(dist值被确定的)，那接下来我们要考虑的问题就是下一个被纳入S的会是谁？ 想一想我们当初是怎么把 1 给纳入的？是不是看了一眼dist数组，发现其他点的dist都是∞，唯独dist[ 1]是一个0，于是把这个 dist最小的点当作了下一个被纳入S的点 。现在我们看一眼dist，发现dist[ 2 ]=1，是最小的一个，于是我们认为 2 才是下一个有资格被纳入S的。

所以，现在问题来了：为什么下一个可以被纳入S的点（dist值可以被确定一定就是最短路径的点），一定就是当前dist最小的点？

我们先来考虑这些个集合S中的点具有什么特性：首先，这些点的dist都是被确定下来的，换句话说，这些点的dist是不会受到S’ 中那些点的影响的，再换句话说，这些点的最短路径上面的所有的点都是在S中了的！

dist被确定 => 不受S’影响 => 最短路径上经过的点都存在与S中了

所以能够被下一个纳入到S中的点，它的最短路径只有可能是S中已经存在的点，不可能是S‘中的点，而当前S’中 dist值最小的点，才会有资格具有这个性质。 为什么？？？

我们可以反证：比方说现在，dist最小的点是2，我们如果假设下一个被纳入S的点不是2，而是5，这也就意味着5才是具有前面提到的那三个性质的点，这个时候的我们是不是也就默认了，2这个点的最短路径有可能会被5的纳入而改变？
因为你选择了纳入5 而不是2 ，也就是你默认了是5的dist被确定了，而不是2，换而言之，你默认了5有可能会在2的最短路径上，但是当前dist[5]=8,dist[ 2 ]=1,怎么可能dist大的那个点会有可能是dist小的那个点的路径上的点？？？（况且现在dist[ 2 ]还是在S’中的，也就意味着它的dist只有可能更小，而dist[ 8 ]已经被确定了）这就产生了悖论！也就是说下一个有资格被纳入S的点，只有可能是dist最小的那个点！这也就是我们所说的路径生成必须要是

非递减序

很多教材在讲到这个非递减序的时候，都是一句带过，很多时候学生们都不理解（比如我emmmm）什么叫做非递减序？为什么要非递减序？这样的好处是什么？我认为理解Dijkstra算法的最关键点就在这个非递减序上，它是Dijkstra算法能成立的最根本的依据。

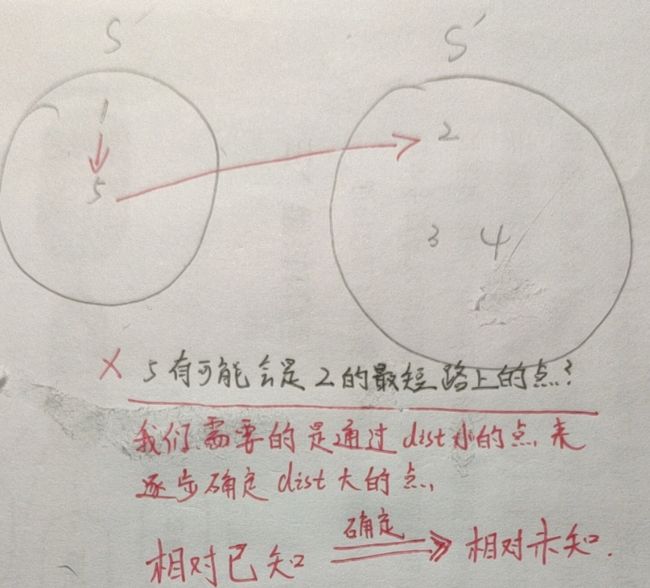
就像我们平时思考问题，是通过当前已知的信息，来猜测、推断未知的事物，不可能通过未知来论证已知，就算不是已知的，我们也会先选择更加有底的事情，也就是相对已知。一个很形象的栗子就是我们中国当初经济发展不就是“先富带动后富”嘛，我们不可能谁都兼顾，我们只能每次都选择“眼前最优”，通过它来带动“眼前次优”，等到所有的”次优“都变成了”最优“，我们这个计划也就达到了”整体最优了“。

咦！这不就是贪心算法嘛~

接下来的问题就显得轻松愉快辽~~~^o^/按照这个道理把剩下的未确定的点一个个取最优确定下来,等到所有点都在S中了,问题也就解决了。

把2纳入S，2和4、5 邻接，且4、5都未在S，比较后更新dist[ 4 ]、dist[ 5 ]

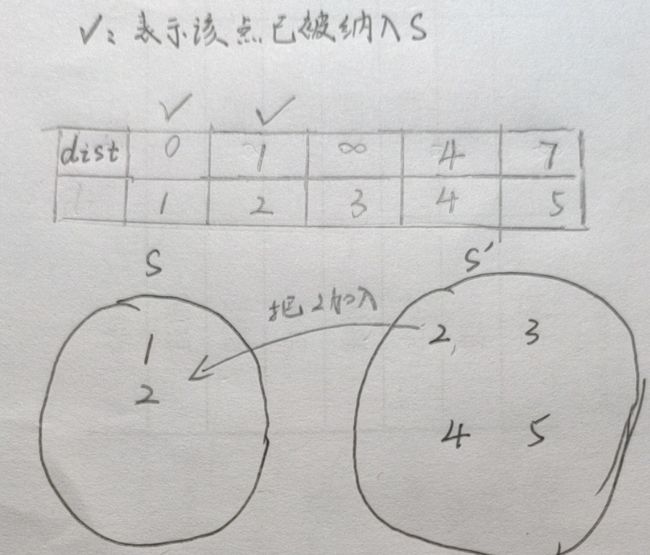
dist[ 4 ]最小，把4纳入，影响到了3、5，把dist[ 3 ]、dist[ 5 ]更新

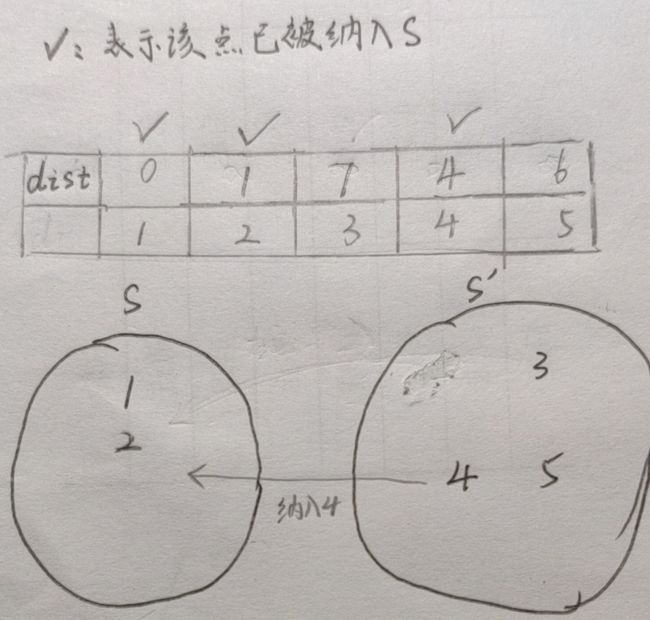
dist[ 5 ]最小，把5纳入，由于dist[ 5 ] + path = = 10 > 7 = = dist[ 3 ],所以dist[ 3 ]不更新

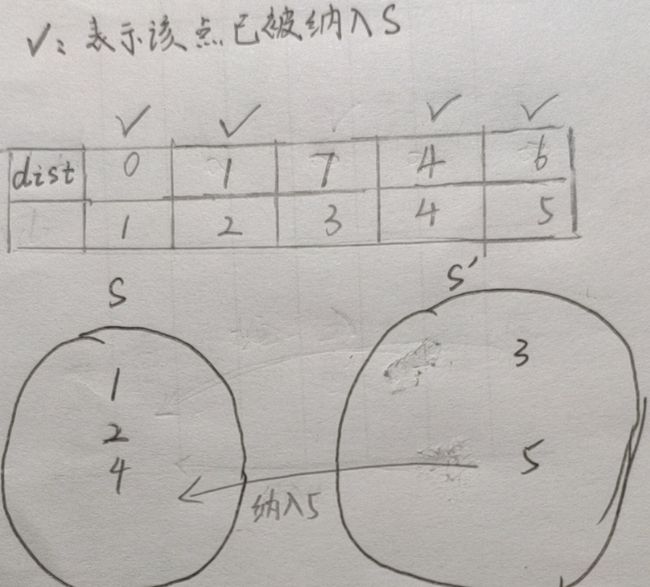
最后把3纳入，其他点都被访问过了，于是没有什么更新的

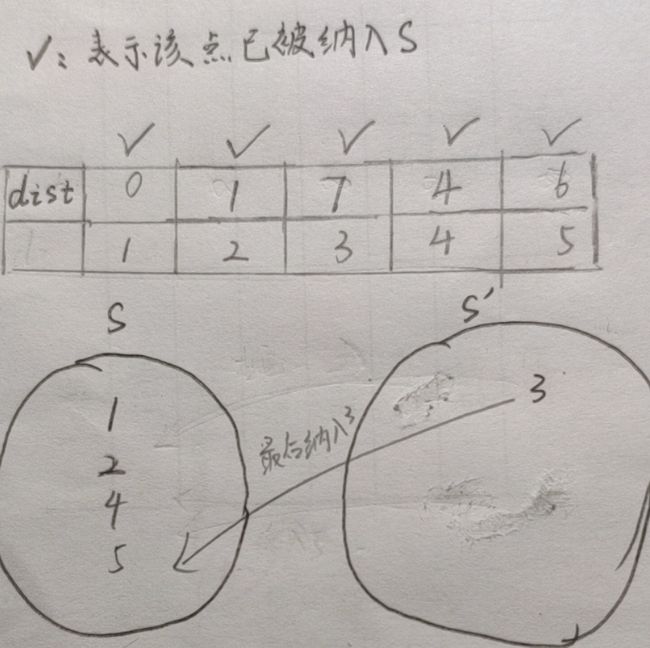
最后发现所有点都在S里了，任务完成(｡･∀･)ﾉ* dist[i]中的便是i到源点的最短路径长度了。

如果要计算最短路径的同时，存下每个点到原点的最短路径是什么，只需要在加上个数组path,每次点a 的dist[a]被其他点b更新，path[a]=b,最后在程序结束的时候用一个栈把迭代的path[a]逆序输出就可以了。

接下来附上Dijkstra算法伪代码：

void Dijkstra( MGraph Graph, int dist[],int path[], Vertex S )
{
	int ask[MaxVertexNum]={0};
	//存储结点是否被访问过，即是否已经在S中
	for(;存在未被纳入到s的结点;)
	{
	int minindex=0;
	
	***在所有未被纳入的点中***
	***找出未被纳入的且dist最小的点***
	***存放到minindex中***
	
	ask[minindex]=1;
	for(所有minindex的邻接点)
	{
		if(dist值更小&&该点未被纳入)
		{
			更新dist
			存储path
		} 
	}
	}
}

那么现在我们来分析一下这个Dijkstra算法的时间复杂度是多少呢？？？
答案是：分析不了( ╯□╰ )…

因为找minindex的方法不资道呀~
1.直接遍历dist数组找minindex：这个方法听起来就很暴力，但是其实挺好的，因为容易写啊…这样的话这个算法就是两个for循环并列，时间复杂度就是O（V^2）,每个被找出来的minindex都会访问它的邻接点，所以时间复杂度也和边数E成正比，因此最终时间复杂度是O（V ^2 + E）.显然，这个方法对于点少边多的稠密图效果不错，而且也容易写。
2.高大上的小顶堆找minindex：将dist数组用小顶堆的形式存放，这样一来找minindex就是一个O（logn）的事情了。但是但是但是——一旦把dist存在小顶堆里，那么我们肯定要维护这个小顶堆，也就是在这个堆里的元素值被改变的时候我们要去调堆，什么时候堆里的元素会被改变？结点纳入S影响到S‘中的dist，所以我们每次改变S’中结点的dist就是一件很麻烦的事情，会变成ElogV这样一来时间复杂度就是 O（VlogV + ElogV)但是我们在这里考虑的是连通图，一般来说边数O（E）>= O（V）点数，所以可以简写成O（ ElogV)。显然这对于稀疏图比较友好。

小声：emmmm,管你稠密不稠密，暴力解法咋看咋亲切╮(╯▽╰)╭

我们这里讨论的是带权的单源最短路，不区分有向、还是无向图，这个权值是什么也是依据现实生活中需要的各种不同情况。
我们大家都用过各种地图app，我们在搜索一个到达目的地的路线的时候，地图会给出达到目的地的几种最优方案，比方说距离最短、开销最小、时间最快…不同的方案，考虑的权值weight就不一样。app给我们反馈用的就是最短路径的算法，只不过比我们学的更加复杂。

砸门再来举个栗子：

城市间紧急救援

作者: 陈越
单位: 浙江大学
时间限制: 400 ms
内存限制: 64 MB
代码长度限制: 16 KB

作为一个城市的应急救援队伍的负责人，你有一张特殊的全国地图。在地图上显示有多个分散的城市和一些连接城市的快速道路。每个城市的救援队数量和每一条连接两个城市的快速道路长度都标在地图上。当其他城市有紧急求助电话给你的时候，你的任务是带领你的救援队尽快赶往事发地，同时，一路上召集尽可能多的救援队。

输入格式:

输入第一行给出4个正整数N、M、S、D，其中N（2≤N≤500）是城市的个数，顺便假设城市的编号为0 ~ (N−1)；M是快速道路的条数；S是出发地的城市编号；D是目的地的城市编号。

第二行给出N个正整数，其中第i个数是第i个城市的救援队的数目，数字间以空格分隔。随后的M行中，每行给出一条快速道路的信息，分别是：城市1、城市2、快速道路的长度，中间用空格分开，数字均为整数且不超过500。输入保证救援可行且最优解唯一。

输出格式:

第一行输出最短路径的条数和能够召集的最多的救援队数量。第二行输出从S到D的路径中经过的城市编号。数字间以空格分隔，输出结尾不能有多余空格。

输入样例:

4 5 0 3
20 30 40 10
0 1 1
1 3 2
0 3 3
0 2 2
2 3 2

输出样例:

2 60
0 1 3

姥姥出的题，一看就很有意思。扫眼题目就知道似一个单源最短路径的问题，核心就是运用Dijkstra算法，只不过多了一个救援队数量和一个路径条数计算，主要关键字是最短路径，次要关键字是队伍召集的数量，题目已经明确告诉你救援可行且最优解唯一，也就是最短路径有多条的情况下，队伍数目肯定有最多的。
虽然源点和终点已经是知道了的，但是不可以在找到终点D的时候就结束，这时候的路径还不一定最优。

代码如下：

#include 
#include 

#define INFINITY 1000000
#define MaxVertexNum 500  /* maximum number of vertices */
typedef int Vertex;      /* vertices are numbered from 0 to MaxVertexNum-1 */
typedef int WeightType;

typedef struct GNode *PtrToGNode;
struct GNode{
    int Nv;
    int Ne;
    WeightType G[MaxVertexNum][MaxVertexNum];
};
typedef PtrToGNode MGraph;

MGraph ReadG(int N,int M)
{
    MGraph G=(MGraph)malloc(sizeof(struct GNode));
   G->Nv=N;
   G->Ne=M;
    int i,j;
    for(i=0;i<G->Nv;i++)
    {
        for(j=0;j<G->Nv;j++)
        {
            G->G[i][j]=INFINITY;
            if(i==j)
                G->G[i][j]=0;
        }
    }
    for(i=0;i<G->Ne;i++)
    {
        int a,b,x;
        scanf("%d%d%d",&a,&b,&x);
        G->G[a][b]=x;
        G->G[b][a]=x;
    }

    return G;
}
void ShortestDist( MGraph Graph, int dist[], int count[], Vertex S ,int path[],int *team,const int *oldteam)
{
    int i,j;

    int ask[MaxVertexNum];
    for(i=0;i<MaxVertexNum;i++)
    ask[i]=0;
    while(1)
    {
        int min=INFINITY;
        int minindex=0;
        int flag=1;
        for(i=0;i<Graph->Nv;i++)
        {
            if(!ask[i])
            {
                flag=0;
                if(dist[i]<=min)
                {
                    minindex=i;
                    min=dist[i];
                }
            }
        }
        if(flag)break;
        ask[minindex]=1;
        for(i=0;i<Graph->Nv;i++)
        {
            if(Graph->G[minindex][i]!=INFINITY&&i!=minindex)
            {
                if((dist[minindex]+Graph->G[minindex][i])<dist[i])
                {
                    if(!ask[i])
                    {
                        //dist更新，同时path,team更新
                        dist[i]=dist[minindex]+Graph->G[minindex][i];
                        count[i]=count[minindex];
                        path[i]=minindex;
                        team[i]=oldteam[i]+team[minindex];
                    }
                }
                else if((dist[minindex]+Graph->G[minindex][i])==dist[i])
                {
                    //dist相等时，比较team，team大的那个是新的path
                    count[i]+=count[minindex];
                    if(team[i]<oldteam[i]+team[minindex]) {
                        team[i] = oldteam[i] + team[minindex];
                        path[i] = minindex;
                    }
                }
            }
        }
    }
    for(i=0;i<Graph->Nv;i++)
    {
        if(dist[i]==INFINITY)
        {
            dist[i]=-1;
            count[i]=0;
        }
    }
}
int main()
{
 int N,M,S,D;
 scanf("%d%d%d%d",&N,&M,&S,&D);
 int team[N];
 //team动态存储当前路径下的救援队总数
 int oldteam[N];
 //oldteam为固定的每个城市的救援队数目
 int path[N];
 //最优路径存储
 int count[N];
 //最短路径条数
 int dist[N];
 //最短路径长度
 int i;
 for(i=0;i<N;i++)
 {
     scanf("%d",&team[i]);
     oldteam[i]=team[i];
     count[i]=0;
     path[i]=-1;
     dist[i]=INFINITY;
     if(i==S)
         count[i]=(dist[i]=0)+1;
 }
 MGraph G=ReadG(N,M);
 ShortestDist( G,dist, count,S,path,team,oldteam);
printf("%d %d\n",count[D],team[D]);
//路径逆序输出
int stack[MaxVertexNum+1];
i=D;
int top=-1;
stack[++top]=i;
while(path[i]!=-1)
{
    stack[++top]=path[i];
    i=path[i];
}

int first=1;
while(top!=-1)
{
    if(first==1)
    {
        printf("%d",stack[top--]);
        first++;
    }
    else
        printf(" %d",stack[top--]);
}
printf("\n");

return 0;
}