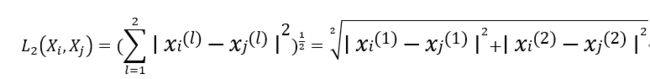机器学习笔记(一)——KNN学习
一、概念:
KNN(K-Nearest Neighber ,简称KNN)学习是一种常用的监督学习方法。
(一)工作机制:
给定测试样本,基于某种距离度量找出训练集中与其最靠近的k个训练样本,然后基于这k个“邻居”的信息来进行预测,其实就是所谓“近朱者赤,近墨者黑”。
(二)训练过程:
KNN学习,没有显式的训练过程,是典型的“懒惰学习”的技术,在训练阶段中仅仅把样本保存起来,训练时间开销为零,待收到测试样本后再进行处理。
二、KNN模型的三个要素
(一)距离度量:
其中两个实例点之间的距离反映了相似程度。
1.曼哈顿距离:
2. 欧氏距离:
(二)K值:
选取样本的数量。
k值的选择会对k近邻法的结果产生重大影响。在应用中,k值一般取一个比较小的数值,通常采用交叉验证法来选取最优的k值。
(三)分类决策的规则:
1.“投票法”:
选择k个样本中出现最多的类别标记为预测结果。
2.“平均法”:
将这k个样本的实值输出标记的平均值作为预测结果。
3.基于距离的投票:
基于距离远近进行加权平均或者加权投票,距离越近的样本权重越大。
三、算法实现
(一)数据准备
import numpy as np
import matplotlib.pyplot as plt
# raw_data_x是特征,raw_data_y是标签,0为良性,1为恶性
raw_data_X = [[3.393533211, 2.331273381],
[3.110073483, 1.781539638],
[1.343853454, 3.368312451],
[3.582294121, 4.679917921],
[2.280362211, 2.866990212],
[7.423436752, 4.685324231],
[5.745231231, 3.532131321],
[9.172112222, 2.511113104],
[7.927841231, 3.421455345],
[7.939831414, 0.791631213]
]
raw_data_y = [0, 0, 0, 0, 0, 1, 1, 1, 1, 1]
# 设置训练组
X_train = np.array(raw_data_X)
y_train = np.array(raw_data_y)
# 将数据可视化
plt.scatter(X_train[y_train==0,0],X_train[y_train==0,1], color='b',label='M',marker = 'x')
plt.scatter(X_train[y_train==1,0],X_train[y_train==1,1], color='r',label='F',marker = '+')
plt.xlabel('Tumor Size')
plt.ylabel('Time')
plt.axis([0,10,0,5])
plt.legend()
plt.show()
(二) 现给定数据
现在给出一个的数据(样本点)x:[8.90933607318, 3.365731514]
1.求距离:
采用欧式方法求距离。
from math import sqrt
x=[8.90933607318, 3.365731514]
distances = [] # 用来记录x到样本数据集中每个点的距离
for x_train in X_train:
d = sqrt(np.sum((x_train - x) ** 2))
distances.append(d)
# 使用列表生成器,一行就能搞定,对于X_train中的每一个元素x_train都进行前面的运算,把结果生成一个列表
distances = [sqrt(np.sum((x_train - x) ** 2)) for x_train in X_train]
在求出距离列表之后,我们要找到最小的距离,需要进行一次排序操作。其实不是简单的排序,因为我们把只将距离排大小是没有意义的,我们要知道距离最小的k个点是在样本集中的位置。
nearest = np.argsort(distances)
输出结果:
array([7, 8, 5, 9, 6, 3, 0, 1, 4, 2], dtype=int32)
2.选k值:
然后我们选择k值,这里暂定为6,那就找出最近的6个点(top 6),并记录他们的标签值(y)
k = 6
topK_y = [y_train[i] for i in nearest[:k]]
topK_y
输出:
[1, 1, 1, 1, 1, 0]
3.分类决策的规则:
下面进入投票环节。找到与测试样本点最近的6个训练样本点的标签y。
from collections import Counter
votes = Counter(topK_y)
votes.most_common(1)
predict_y = votes.most_common(1)[0][0]
最终将样本点预测结果为1。
4.完整代码
(1)kNN.py
import numpy as np
from math import sqrt
from collections import Counter
class kNNClassifier:
def __init__(self, k):
"""初始化分类器"""
assert k >= 1, "k must be valid"
self.k = k
self._X_train = None
self._y_train = None
def fit(self, X_train, y_train):
"""根据训练数据集X_train和y_train训练kNN分类器"""
assert X_train.shape[0] == y_train.shape[0], \
"the size of X_train must be equal to the size of y_train"
assert self.k <= X_train.shape[0], \
"the size of X_train must be at least k"
self._X_train = X_train
self._y_train = y_train
return self
def predict(self,X_predict):
"""给定待预测数据集X_predict,返回表示X_predict结果的向量"""
assert self._X_train is not None and self._y_train is not None, \
"must fit before predict!"
assert X_predict.shape[1] == self._X_train.shape[1], \
"the feature number of X_predict must be equal to X_train"
y_predict = [self._predict(x) for x in X_predict]
return np.array(y_predict)
def _predict(self, x):
distances = [sqrt(np.sum((x_train - x) ** 2)) for x_train in self._X_train]
nearest = np.argsort(distances)
topK_y = [self._y_train[i] for i in nearest]
votes = Counter(topK_y)
return votes.most_common(1)[0][0]
def __repr__(self):
return "kNN(k=%d)" % self.k
(2)调用代码
%run kNN.py
knn_clf = kNNClassifier(k=6)
knn_clf.fit(X_train, y_train)
X_predict = x.reshape(1,-1)
y_predict = knn_clf.predict(X_predict)
y_predict
输出:
array([1])
5. sklearn中的kNN
机器学习其流程是:训练数据集 -> 机器学习算法 -fit-> 模型 输入样例 -> 模型 -predict-> 输出结果
用sklearn中已经封装好的kNN库。
from sklearn.neighbors import KNeighborsClassifier
# 创建kNN_classifier实例
kNN_classifier = KNeighborsClassifier(n_neighbors=6)
# kNN_classifier做一遍fit(拟合)的过程,没有返回值,模型就存储在kNN_classifier实例中
kNN_classifier.fit(X_train, y_train)
# kNN进行预测predict,需要传入一个矩阵,而不能是一个数组。reshape()成一个二维数组,第一个参数是1表示只有一个数据,第二个参数-1,numpy自动决定第二维度有多少
y_predict = kNN_classifier.predict(x.reshape(1,-1))
y_predict
输出:
array([1])
对于KNeighborsClassifier的方法:
- 方法名 含义
-
fit(X, y) 使用X作为训练数据,y作为目标值(类似于标签)来拟合模型。
get_params([deep]) 获取估值器的参数。
neighbors([X, n_neighbors, return_distance]) 查找一个或几个点的K个邻居。
kneighbors_graph([X, n_neighbors, mode]) 计算在X数组中每个点的k邻居的(权重)图。
predict(X) 给提供的数据预测对应的标签。
predict_proba(X) 返回测试数据X的概率估值。
score(X, y[, sample_weight]) 返回给定测试数据和标签的平均准确值。
set_params(**params) 设置估值器的参数。
四、总结:
(一)kNN原理:
KNN是一种即可用于分类又可用于回归的机器学习算法。对于给定测试样本,基于距离度量找出训练集中与其最靠近的K个训练样本,然后基于这K个“邻居”的信息来进行预测。
在分类任务中可使用投票法,选择这K个样本中出现最多的类别标记作为预测结果;在回归任务中可使用平均法,将这K个样本的实值输出标记的平均值作为预测结果。当然还可以基于距离远近程度进行加权平均等方法。
(二)优缺点:
优点:
算法简单,既可以用来做分类也可以用来做回归
由于KNN方法主要靠周围有限的邻近的样本,对于类域的交叉或重叠较多的待分样本集来说,KNN方法较其他方法更为适合
该算法比较适用于样本容量比较大的类域的自动分类
缺点:
特征数非常多的时候,计算量大
样本不平衡的时候,对稀有类别的预测准确率低
使用懒散学习方法,基本上不学习,导致预测时速度比起逻辑回归之类的算法慢
(三)kNN如何计算距离,为什么使用欧式距离而非曼哈顿距离?
预测点与所有的距离进行计算,然后对距离进行排序,选择前K个值类别较多的。
曼哈顿距离只计算维度内的距离。
而欧式距离计算多维空间的直接距离。
因此欧式距离为最佳选择。
(四)k值选择:
k值一般取一个比较小的数值,可采用交叉验证法(简单来说,就是一部分样本做训练集,一部分做测试集)来选择最优的k值。
(五)kNN时间复杂度:
KNN算法的时间复杂度为O(DNN)。其中D为维度数,N为样本总数。从时间复杂度上,一般适用于样本数较少的数据集,非常不适合高维度的数据集。