神经网络模型应用实例SPSS - 典型的神经网络模型 - 神经网络模型的应用

神经网络算法实例说明有哪些？

在网络模型与算法研究的基础上，利用人工神经网络组成实际的应用系统，例如，完成某种信号处理或模式识别的功能、构作专家系统、制成机器人、复杂系统控制等等。

纵观当代新兴科学技术的发展历史，人类在征服宇宙空间、基本粒子，生命起源等科学技术领域的进程中历经了崎岖不平的道路。我们也会看到，探索人脑功能和神经网络的研究将伴随着重重困难的克服而日新月异。

神经网络ART1模型

一、ART1模型概述

自适应共振理论(Adaptive Resonance Theory)简称ART，是于1976年由美国Boston大学S.Grossberg提出来的。

这一理论的显著特点是，充分利用了生物神经细胞之间自兴奋与侧抑制的动力学原理，让输入模式通过网络双向连接权的识别与比较，最后达到共振来完成对自身的记忆，并以同样的方法实现网络的回想。当提供给网络回想的是一个网络中记忆的、或是与已记忆的模式十分相似的模式时，网络将会把这个模式回想出来，提出正确的分类。如果提供给网络回想的是一个网络中不存在的模式，则网络将在不影响已有记忆的前提下，将这一模式记忆下来，并将分配一个新的分类单元作为这一记忆模式的分类标志。

S.Grossberg和G.A.Carpenter经过多年研究和不断发展，至今已提出了ART1，ART2和ART3三种网络结构。

ART1网络处理双极型(或二进制)数据，即观察矢量的分量是二值的，它只取0或1。

二、ART1模型原理

ART1网络是两层结构，分输入层(比较层)和输出层(识别层)。从输入层到输出层由前馈连接权连接，从输出层到输入层由反馈连接权连接。

设网络输入层有N个神经元，网络输出层有M个神经元，二值输入模式和输出向量分别为：Xp=( 。

，

，…，

)，Yp=(

，

，…，

)，p=1，2，…，P，其中P为输入学习模式的个数。设前馈连接权和反馈连接权矩阵分别为W=(wnm)N×M，T=(tnm)N×M，n=1，2，…，N，m=1，2，…，M。

ART1网络的学习及工作过程，是通过反复地将输入学习模式由输入层向输出层自下而上的识别和由输出层向输入层自上而下的比较过程来实现的。当这种自下而上的识别和自上而下的比较达到共振，即输出向量可以正确反映输入学习模式的分类，且网络原有记忆没有受到不良影响时，网络对一个输入学习模式的记忆分类则告完成。

ART1网络的学习及工作过程，可以分为初始化阶段、识别阶段、比较阶段和探寻阶段。

1.初始化阶段

ART1网络需要初始化的参数主要有3个：

即W=(wnm)N×M，T=(tnm)N×M和ρ。

反馈连接权T=(tnm)N×M在网络的整个学习过程中取0或1二值形式。这一参数实际上反映了输入层和输出层之间反馈比较的范围或强度。由于网络在初始化前没有任何记忆，相当于一张白纸，即没有选择比较的余的。因此可将T的元素全部设置为1，即。

tnm=1，n=1，2，…，N，m=1，2，…，M。(1)。

这意味着网络在初始状态时，输入层和输出层之间将进行全范围比较，随着学习过程的深入，再按一定规则选择比较范围。

前馈连接权W=(wnm)N×M在网络学习结束后，承担着对学习模式的记忆任务。在对W初始化时，应该给所有学习模式提供一个平等竞争的机会，然后通过对输入模式的竞争，按一定规则调整W。W的初始值按下式设置：

中国矿产资源评价新技术与评价新模型。

ρ称为网络的警戒参数，其取值范围为0＜ρ≤1。

2.识别阶段

ART1网络的学习识别阶段发生在输入学习模式由输入层向输出层的传递过程中。在这一阶段，首先将一个输入学习模式Xp=( 。

，

，…，

)提供给网络的输入层，然后把作为输入学习模式的存储媒介的前馈连接权W=(wnm)N×M与表示对这一输入学习模式分类结果的输出层的各个神经元进行比较，以寻找代表正确分类结果的神经元g。这一比较与寻找过程是通过寻找输出层神经元最大加权输入值，即神经元之间的竞争过程实现的，如下式所示：

中国矿产资源评价新技术与评价新模型。

中国矿产资源评价新技术与评价新模型。

中国矿产资源评价新技术与评价新模型。

至此，网络的识别过程只是告一段落，并没有最后结束。此时，神经元m=g是否真正有资格代表对输入学习模式Xp的正确分类，还有待于下面的比较和寻找阶段来进一步确定。一般情况下需要对代表同一输入学习模式的分类结果的神经元进行反复识别。

3.比较阶段

ART1网络的比较阶段的主要职能是完成以下检查任务，每当给已学习结束的网络提供一个供识别的输入模式时，首先检查一下这个模式是否是已学习过的模式，如果是，则让网络回想出这个模式的分类结果；如果不是，则对这个模式加以记忆，并分配一个还没有利用过的输出层神经元来代表这个模式的分类结果。

具体过程如下：把由输出层每个神经元反馈到输入层的各个神经元的反馈连接权向量Tm=(t1m，t2m，…，tNm)，m=1，2，…，M作为对已学习的输入模式的一条条记录，即让向量Tm=(t1m，t2m，…，tNm)与输出层第m个神经元所代表的某一学习输入模式Xp=( 。

，

，…，

)完全相等。

当需要网络对某个输入模式进行回想时，这个输入模式经过识别阶段，竞争到神经元g作为自己的分类结果后，要检查神经元g反馈回来的向量Tg是否与输入模式相等。如果相等，则说明这是一个已记忆过的模式，神经元g代表了这个模式的分类结果，识别与比较产生了共振，网络不需要再经过寻找阶段，直接进入下一个输入模式的识别阶段；如果不相符，则放弃神经元g的分类结果，进入寻找阶段。

在比较阶段，当用向量Tg与输入模式XP进行比较时，允许二者之间有一定的差距，差距的大小由警戒参数ρ决定。

首先计算

中国矿产资源评价新技术与评价新模型。

Cg表示向量Tg与输入模式XP的拟合度。

在式中，

(tng*xn)表示向量Tg=(t1g，t2g，…，tNg)与输入模式Xp=( 。

，

，…，

)的逻辑“与”。

当Tg=XP时，Cg=1。

当Cg≥ρ时，说明拟合度大于要求，没有超过警戒线。

以上两种情况均可以承认识别结果。

当Cg≠1且Cg＞ρ时，按式(6)式(7)将前馈连接权Wg=(w1g，w2g，…，wNg)和反馈连接权Tg=(t1g，t2g，…，tNg)向着与XP更接近的方向调整。

中国矿产资源评价新技术与评价新模型。

tng(t+1)=tng(t)*xn，n=1，2，…，N。(7)。

当Cg＜ρ时，说明拟合度小于要求，超过警戒线，则拒绝识别结果，将神经元g重新复位为0，并将这个神经元排除在下次识别范围之外，网络转入寻找阶段。

4.寻找阶段

寻找阶段是网络在比较阶段拒绝识别结果之后转入的一个反复探寻的阶段，在这一阶段中，网络将在余下的输出层神经元中搜索输入模式Xp的恰当分类。只要在输出向量Yp=( 。

，

，…

)中含有与这一输入模式Xp相对应、或在警戒线以内相对应的分类单元，则网络可以得到与记忆模式相符的分类结果。如果在已记忆的分类结果中找不到与现在输入的模式相对应的分类，但在输出向量中还有未曾使用过的单元，则可以给这个输入模式分配一个新的分类单元。在以上两种情况下，网络的寻找过程总能获得成功，也就是说共振终将发生。

三、总体算法

设网络输入层有N个神经元，网络输出层有M个神经元，二值输入模式和输出向量分别为：Xp=( 。

，

，…，

)，Yp=(

，

，…，

)p=1，2，…，p，其中p为输入学习模式的个数。设前馈连接权和反馈连接权矩阵分别为W=(wnm)N×M，T=(tnm)N×M，n=1，2，…，N，m=1，2，…，M。

(1)网络初始化

tnm(0)=1，

中国矿产资源评价新技术与评价新模型。

n=1，2，…，N，m=1，2，…，M。

0＜ρ≤1。

(2)将输入模式Xp=(

，

，…，

)提供给网络的输入层

(3)计算输出层各神经元输入加权和。

中国矿产资源评价新技术与评价新模型。

(4)选择XP的最佳分类结果

中国矿产资源评价新技术与评价新模型。

令神经元g的输出为1。

(5)计算

中国矿产资源评价新技术与评价新模型。

中国矿产资源评价新技术与评价新模型。

判断

中国矿产资源评价新技术与评价新模型。

当式(8)成立，转到(7)，否则，转到(6)。

(6)取消识别结果，将输出层神经元g的输出值复位为0，并将这一神经元排除在下一次识别的范围之外，返回步骤(4)。当所有已利用过的神经元都无法满足式(8)，则选择一个新的神经元作为分类结果，转到步骤(7)。

(7)承认识别结果，并按下式调整连接权。

中国矿产资源评价新技术与评价新模型。

tng(t+1)=tng(t)*xn，n=1，2，…，N。

(8)将步骤(6)复位的所有神经元重新加入识别范围之内，返回步骤(2)对下一模式进行识别。

(9)输出分类识别结果。

(10)结束。

四、实例

实例为ART1神经网络模型在柴北缘-东昆仑造山型金矿预测的应用。

1.建立综合预测模型

柴北缘—东昆仑地区位于青海省的西部，是中央造山带的西部成员——秦祁昆褶皱系的一部分，是典型的复合造山带(殷鸿福等，1998)。根据柴北缘—东昆仑地区地质概括以及造山型金矿成矿特点，选择与成矿相关密切的专题数据，建立柴北缘—东昆仑地区的综合信息找矿模型：

1)金矿重砂异常数据是金矿的重要找矿标志。

2)金矿水化异常数据是金矿的重要找矿标志。

3)金矿的化探异常数据控制金矿床的分布。

4)金矿的空间分布与通过该区的深大断裂有关。

5)研究区内断裂密集程度控制金矿的产出。

6)重力构造的存在与否是金矿存在的一个标志。

7)磁力构造线的存在也是金矿存在的一个重要标志。

8)研究区地质复杂程度也对金矿的产出具有重要的作用。

9)研究区存在的矿(化)点是一个重要的标志。

2.划分预测单元

预测工作是在单元上进行的，预测工作的结果是与单元有着较为直接的联系，在找矿模型指导下，以最大限度地反映成矿信息和预测单元面积最小为原则，通过对研究区内地质、地球物理、地球化学等的综合资料分析，对可能的成矿地段圈定了预测单元。采用网格化单元作为本次研究的预测单元，网格单元的大小是，40×40，将研究区划分成774个预测单元。

3.变量选择(表8-6)

4.ART1模型预测结果

ART1神经网络模型算法中，给定不同的阈值，将改变预测分类的结果。本次实验选取得阈值为ρ=0.41，系统根据此阈值进行计算获得计算结果，并通过将不同的分类结果赋予不同的颜色，最终获得ART模型预测单元的分类结果。分类的结果是形成29个类别。分类结果用不同的颜色表示，其具体结果地显示见图8-5。图形中颜色只代表类别号，不代表分类的好坏。将矿点专题图层叠加以后，可以看出，颜色为灰色的单元与矿的关系更为密切。

表8-6 预测变量标志的选择表。

图8-5 东昆仑—柴北缘地区基于ARTL模型的金矿分类结果图。

AI爱发猫

matlab神经网络目前有什么具体的实际应用

人工神经网络研究目前主要分两类：理论研究和应用研究。

理论研究方面，①利用神经生理与认知科学研究人类思维以及智能机理；②利用神经基础理论的研究成果，用数理方法探索功能更加完善、性能更加优越的神经网络模型，深入研究网络算法和性能。开发新的网络数理理论，如神经网络动力学、非线性神经场等等。

应用研究方面，①神经网络的软件模拟和硬件实现的研究；②神经网络在各个领域中应用的研究。如，模式识别、信号处理、专家系统、机器人控制等等。

神经网络BP模型

一、BP模型概述

误差逆传播(Error Back-Propagation)神经网络模型简称为BP(Back-Propagation)网络模型。

Pall Werbas博士于1974年在他的博士论文中提出了误差逆传播学习算法。完整提出并被广泛接受误差逆传播学习算法的是以Rumelhart和McCelland为首的科学家小组。他们在1986年出版“Parallel Distributed Processing，Explorations in the Microstructure of Cognition”(《并行分布信息处理》)一书中，对误差逆传播学习算法进行了详尽的分析与介绍，并对这一算法的潜在能力进行了深入探讨。

BP网络是一种具有3层或3层以上的阶层型神经网络。上、下层之间各神经元实现全连接，即下层的每一个神经元与上层的每一个神经元都实现权连接，而每一层各神经元之间无连接。网络按有教师示教的方式进行学习，当一对学习模式提供给网络后，神经元的激活值从输入层经各隐含层向输出层传播，在输出层的各神经元获得网络的输入响应。在这之后，按减小期望输出与实际输出的误差的方向，从输入层经各隐含层逐层修正各连接权，最后回到输入层，故得名“误差逆传播学习算法”。随着这种误差逆传播修正的不断进行，网络对输入模式响应的正确率也不断提高。

BP网络主要应用于以下几个方面：

1)函数逼近：用输入模式与相应的期望输出模式学习一个网络逼近一个函数；

2)模式识别：用一个特定的期望输出模式将它与输入模式联系起来；

3)分类：把输入模式以所定义的合适方式进行分类；

4)数据压缩：减少输出矢量的维数以便于传输或存储。

在人工神经网络的实际应用中，80%～90%的人工神经网络模型采用BP网络或它的变化形式，它也是前向网络的核心部分，体现了人工神经网络最精华的部分。

二、BP模型原理

下面以三层BP网络为例，说明学习和应用的原理。

1.数据定义

P对学习模式(xp，dp)，p=1，2，…，P；

输入模式矩阵X[N][P]=(x1，x2，…，xP)；

目标模式矩阵d[M][P]=(d1，d2，…，dP)。

三层BP网络结构

输入层神经元节点数S0=N，i=1，2，…，S0；

隐含层神经元节点数S1，j=1，2，…，S1；

神经元激活函数f1[S1]；

权值矩阵W1[S1][S0]；

偏差向量b1[S1]。

输出层神经元节点数S2=M，k=1，2，…，S2；

神经元激活函数f2[S2]；

权值矩阵W2[S2][S1]；

偏差向量b2[S2]。

学习参数

目标误差ϵ；

初始权更新值Δ0；

最大权更新值Δmax；

权更新值增大倍数η+；

权更新值减小倍数η-。

2.误差函数定义

对第p个输入模式的误差的计算公式为。

中国矿产资源评价新技术与评价新模型。

y2kp为BP网的计算输出。

3.BP网络学习公式推导

BP网络学习公式推导的指导思想是，对网络的权值W、偏差b修正，使误差函数沿负梯度方向下降，直到网络输出误差精度达到目标精度要求，学习结束。

各层输出计算公式

输入层

y0i=xi，i=1，2，…，S0；

隐含层

中国矿产资源评价新技术与评价新模型。

y1j=f1(z1j)，

j=1，2，…，S1；

输出层

中国矿产资源评价新技术与评价新模型。

y2k=f2(z2k)，

k=1，2，…，S2。

输出节点的误差公式

中国矿产资源评价新技术与评价新模型。

对输出层节点的梯度公式推导

中国矿产资源评价新技术与评价新模型。

E是多个y2m的函数，但只有一个y2k与wkj有关，各y2m间相互独立。

其中

中国矿产资源评价新技术与评价新模型。

则

中国矿产资源评价新技术与评价新模型。

设输出层节点误差为

δ2k=(dk-y2k)·f2′(z2k)，

则

中国矿产资源评价新技术与评价新模型。

同理可得

中国矿产资源评价新技术与评价新模型。

对隐含层节点的梯度公式推导

中国矿产资源评价新技术与评价新模型。

E是多个y2k的函数，针对某一个w1ji，对应一个y1j，它与所有的y2k有关。因此，上式只存在对k的求和，其中。

中国矿产资源评价新技术与评价新模型。

则

中国矿产资源评价新技术与评价新模型。

设隐含层节点误差为

中国矿产资源评价新技术与评价新模型。

则

中国矿产资源评价新技术与评价新模型。

同理可得

中国矿产资源评价新技术与评价新模型。

4.采用弹性BP算法(RPROP)计算权值W、偏差b的修正值ΔW，Δb。

1993年德国 Martin Riedmiller和Heinrich Braun 在他们的论文“A Direct Adaptive Method for Faster Backpropagation Learning：The RPROP Algorithm”中，提出Resilient Backpropagation算法——弹性BP算法(RPROP)。这种方法试图消除梯度的大小对权步的有害影响，因此，只有梯度的符号被认为表示权更新的方向。

权改变的大小仅仅由权专门的“更新值”

确定

中国矿产资源评价新技术与评价新模型。

其中

表示在模式集的所有模式(批学习)上求和的梯度信息，(t)表示t时刻或第t次学习。

权更新遵循规则：如果导数是正(增加误差)，这个权由它的更新值减少。如果导数是负，更新值增加。

中国矿产资源评价新技术与评价新模型。

RPROP算法是根据局部梯度信息实现权步的直接修改。对于每个权，我们引入它的。

各自的更新值

，它独自确定权更新值的大小。这是基于符号相关的自适应过程，它基。

于在误差函数E上的局部梯度信息，按照以下的学习规则更新。

中国矿产资源评价新技术与评价新模型。

其中0＜η-＜1＜η+。

在每个时刻，如果目标函数的梯度改变它的符号，它表示最后的更新太大，更新值 。

应由权更新值减小倍数因子η-得到减少；如果目标函数的梯度保持它的符号，更新值应由权更新值增大倍数因子η+得到增大。

为了减少自由地可调参数的数目，增大倍数因子η+和减小倍数因子η–被设置到固定值。

η+=1.2，

η-=0.5，

这两个值在大量的实践中得到了很好的效果。

RPROP算法采用了两个参数：初始权更新值Δ0和最大权更新值Δmax。

当学习开始时，所有的更新值被设置为初始值Δ0，因为它直接确定了前面权步的大小，它应该按照权自身的初值进行选择，例如，Δ0=0.1(默认设置)。

为了使权不至于变得太大，设置最大权更新值限制Δmax，默认上界设置为。

Δmax=50.0。

在很多实验中，发现通过设置最大权更新值Δmax到相当小的值，例如。

Δmax=1.0。

我们可能达到误差减小的平滑性能。

5.计算修正权值W、偏差b

第t次学习，权值W、偏差b的的修正公式。

W(t)=W(t-1)+ΔW(t)，

b(t)=b(t-1)+Δb(t)，

其中，t为学习次数。

6.BP网络学习成功结束条件每次学习累积误差平方和。

中国矿产资源评价新技术与评价新模型。

每次学习平均误差

中国矿产资源评价新技术与评价新模型。

当平均误差MSE＜ε，BP网络学习成功结束。

7.BP网络应用预测

在应用BP网络时，提供网络输入给输入层，应用给定的BP网络及BP网络学习得到的权值W、偏差b，网络输入经过从输入层经各隐含层向输出层的“顺传播”过程，计算出BP网的预测输出。

8.神经元激活函数f

线性函数

f(x)=x，

f′(x)=1，

f(x)的输入范围(-∞，+∞)，输出范围(-∞，+∞)。

一般用于输出层，可使网络输出任何值。

S型函数S(x)

中国矿产资源评价新技术与评价新模型。

f(x)的输入范围(-∞，+∞)，输出范围(0，1)。

f′(x)=f(x)[1-f(x)]，

f′(x)的输入范围(-∞，+∞)，输出范围(0，

]。

一般用于隐含层，可使范围(-∞，+∞)的输入，变成(0，1)的网络输出，对较大的输入，放大系数较小；而对较小的输入，放大系数较大，所以可用来处理和逼近非线性的输入/输出关系。

在用于模式识别时，可用于输出层，产生逼近于0或1的二值输出。

双曲正切S型函数

中国矿产资源评价新技术与评价新模型。

f(x)的输入范围(-∞，+∞)，输出范围(-1，1)。

f′(x)=1-f(x)·f(x)，

f′(x)的输入范围(-∞，+∞)，输出范围(0，1]。

一般用于隐含层，可使范围(-∞，+∞)的输入，变成(-1，1)的网络输出，对较大的输入，放大系数较小；而对较小的输入，放大系数较大，所以可用来处理和逼近非线性的输入/输出关系。

阶梯函数

类型1

中国矿产资源评价新技术与评价新模型。

f(x)的输入范围(-∞，+∞)，输出范围{0，1}。

f′(x)=0。

类型2

中国矿产资源评价新技术与评价新模型。

f(x)的输入范围(-∞，+∞)，输出范围{-1，1}。

f′(x)=0。

斜坡函数

类型1

中国矿产资源评价新技术与评价新模型。

f(x)的输入范围(-∞，+∞)，输出范围[0，1]。

中国矿产资源评价新技术与评价新模型。

f′(x)的输入范围(-∞，+∞)，输出范围{0，1}。

类型2

中国矿产资源评价新技术与评价新模型。

f(x)的输入范围(-∞，+∞)，输出范围[-1，1]。

中国矿产资源评价新技术与评价新模型。

f′(x)的输入范围(-∞，+∞)，输出范围{0，1}。

三、总体算法

1.三层BP网络(含输入层，隐含层，输出层)权值W、偏差b初始化总体算法。

(1)输入参数X[N][P]，S0，S1，f1[S1]，S2，f2[S2]；

(2)计算输入模式X[N][P]各个变量的最大值，最小值矩阵 Xmax[N]，Xmin[N]；

(3)隐含层的权值W1，偏差b1初始化。

情形1：隐含层激活函数f( )都是双曲正切S型函数。

1)计算输入模式X[N][P]的每个变量的范围向量Xrng[N]；

2)计算输入模式X的每个变量的范围均值向量Xmid[N]；

3)计算W，b的幅度因子Wmag；

4)产生[-1，1]之间均匀分布的S0×1维随机数矩阵Rand[S1]；

5)产生均值为0，方差为1的正态分布的S1×S0维随机数矩阵Randnr[S1][S0]，随机数范围大致在[-1，1]；

6)计算W[S1][S0]，b[S1]；

7)计算隐含层的初始化权值W1[S1][S0]；

8)计算隐含层的初始化偏差b1[S1]；

9))输出W1[S1][S0]，b1[S1]。

情形2：隐含层激活函数f( )都是S型函数。

1)计算输入模式X[N][P]的每个变量的范围向量Xrng[N]；

2)计算输入模式X的每个变量的范围均值向量Xmid[N]；

3)计算W，b的幅度因子Wmag；

4)产生[-1，1]之间均匀分布的S0×1维随机数矩阵Rand[S1]；

5)产生均值为0，方差为1的正态分布的S1×S0维随机数矩阵Randnr[S1][S0]，随机数范围大致在[-1，1]；

6)计算W[S1][S0]，b[S1]；

7)计算隐含层的初始化权值W1[S1][S0]；

8)计算隐含层的初始化偏差b1[S1]；

9)输出W1[S1][S0]，b1[S1]。

情形3：隐含层激活函数f( )为其他函数的情形。

1)计算输入模式X[N][P]的每个变量的范围向量Xrng[N]；

2)计算输入模式X的每个变量的范围均值向量Xmid[N]；

3)计算W，b的幅度因子Wmag；

4)产生[-1，1]之间均匀分布的S0×1维随机数矩阵Rand[S1]；

5)产生均值为0，方差为1的正态分布的S1×S0维随机数矩阵Randnr[S1][S0]，随机数范围大致在[-1，1]；

6)计算W[S1][S0]，b[S1]；

7)计算隐含层的初始化权值W1[S1][S0]；

8)计算隐含层的初始化偏差b1[S1]；

9)输出W1[S1][S0]，b1[S1]。

(4)输出层的权值W2，偏差b2初始化。

1)产生[-1，1]之间均匀分布的S2×S1维随机数矩阵W2[S2][S1]；

2)产生[-1，1]之间均匀分布的S2×1维随机数矩阵b2[S2]；

3)输出W2[S2][S1]，b2[S2]。

2.应用弹性BP算法(RPROP)学习三层BP网络(含输入层，隐含层，输出层)权值W、偏差b总体算法。

函数：Train3BP_RPROP(S0，X，P，S1，W1，b1，f1，S2，W2，b2，f2，d，TP)。

(1)输入参数

P对模式(xp，dp)，p=1，2，…，P；

三层BP网络结构；

学习参数。

(2)学习初始化

1)

；

2)各层W，b的梯度值

，

初始化为零矩阵。

(3)由输入模式X求第一次学习各层输出y0，y1，y2及第一次学习平均误差MSE。

(4)进入学习循环

epoch=1

(5)判断每次学习误差是否达到目标误差要求。

如果MSE＜ϵ，

则，跳出epoch循环，

转到(12)。

(6)保存第epoch-1次学习产生的各层W，b的梯度值 。

，

(7)求第epoch次学习各层W，b的梯度值 。

，

1)求各层误差反向传播值δ；

2)求第p次各层W，b的梯度值 。

，

；

3)求p=1，2，…，P次模式产生的W，b的梯度值 。

，

的累加。

(8)如果epoch=1，则将第epoch-1次学习的各层W，b的梯度值 。

，

设为第epoch次学习产生的各层W，b的梯度值 。

，

。

(9)求各层W，b的更新

1)求权更新值Δij更新；

2)求W，b的权更新值

，

；

3)求第epoch次学习修正后的各层W，b。

(10)用修正后各层W、b，由X求第epoch次学习各层输出y0，y1，y2及第epoch次学习误差MSE。

(11)epoch=epoch+1，

如果epoch≤MAX_EPOCH，转到(5)；

否则，转到(12)。

(12)输出处理

1)如果MSE＜ε，

则学习达到目标误差要求，输出W1，b1，W2，b2。

2)如果MSE≥ε，

则学习没有达到目标误差要求，再次学习。

(13)结束

3.三层BP网络(含输入层，隐含层，输出层)预测总体算法。

首先应用Train3lBP_RPROP( )学习三层BP网络(含输入层，隐含层，输出层)权值W、偏差b，然后应用三层BP网络(含输入层，隐含层，输出层)预测。

函数：Simu3lBP( )。

1)输入参数：

P个需预测的输入数据向量xp，p=1，2，…，P；

三层BP网络结构；

学习得到的各层权值W、偏差b。

2)计算P个需预测的输入数据向量xp(p=1，2，…，P)的网络输出 y2[S2][P]，输出预测结果y2[S2][P]。

四、总体算法流程图

BP网络总体算法流程图见附图2。

五、数据流图

BP网数据流图见附图1。

六、实例

实例一 全国铜矿化探异常数据BP 模型分类。

1.全国铜矿化探异常数据准备

在全国铜矿化探数据上用稳健统计学方法选取铜异常下限值33.1，生成全国铜矿化探异常数据。

2.模型数据准备

根据全国铜矿化探异常数据，选取7类33个矿点的化探数据作为模型数据。这7类分别是岩浆岩型铜矿、斑岩型铜矿、矽卡岩型、海相火山型铜矿、陆相火山型铜矿、受变质型铜矿、海相沉积型铜矿，另添加了一类没有铜异常的模型(表8-1)。

3.测试数据准备

全国化探数据作为测试数据集。

4.BP网络结构

隐层数2，输入层到输出层向量维数分别为14，9、5、1。学习率设置为0.9，系统误差1e-5。没有动量项。

表8-1 模型数据表

续表

5.计算结果图

如图8-2、图8-3。

图8-2

图8-3 全国铜矿矿床类型BP模型分类示意图。

实例二 全国金矿矿石量品位数据BP 模型分类。

1.模型数据准备

根据全国金矿储量品位数据，选取4类34个矿床数据作为模型数据，这4类分别是绿岩型金矿、与中酸性浸入岩有关的热液型金矿、微细浸染型型金矿、火山热液型金矿(表8-2)。

2.测试数据准备

模型样本点和部分金矿点金属量、矿石量、品位数据作为测试数据集。

3.BP网络结构

输入层为三维，隐层1层，隐层为三维，输出层为四维，学习率设置为0.8，系统误差1e-4，迭代次数5000。

表8-2 模型数据

4.计算结果

结果见表8-3、8-4。

表8-3 训练学习结果

表8-4 预测结果(部分)

续表

神经网络原理及应用

神经网络原理及应用

1. 什么是神经网络？

神经网络是一种模拟动物神经网络行为特征，进行分布式并行信息处理的算法。这种网络依靠系统的复杂程度，通过调整内部大量节点之间相互连接的关系，从而达到处理信息的目的。

人类的神经网络

2. 神经网络基础知识。

构成：大量简单的基础元件——神经元相互连接。

工作原理：模拟生物的神经处理信息的方式。

功能：进行信息的并行处理和非线性转化。

特点：比较轻松地实现非线性映射过程，具有大规模的计算能力。

神经网络的本质：

神经网络的本质就是利用计算机语言模拟人类大脑做决定的过程。

3. 生物神经元结构。

4. 神经元结构模型。

xj为输入信号，θi为阈值，wij表示与神经元连接的权值，yi表示输出值。

判断xjwij是否大于阈值θi。

5. 什么是阈值？

临界值。

神经网络是模仿大脑的神经元，当外界刺激达到一定的阈值时，神经元才会受刺激，影响下一个神经元。

6. 几种代表性的网络模型。

单层前向神经网络——线性网络

阶跃网络

多层前向神经网络（反推学习规则即BP神经网络）

Elman网络、Hopfield网络、双向联想记忆网络、自组织竞争网络等等。

7. 神经网络能干什么？

运用这些网络模型可实现函数逼近、数据聚类、模式分类、优化计算等功能。因此，神经网络广泛应用于人工智能、自动控制、机器人、统计学等领域的信息处理中。虽然神经网络的应用很广，但是在具体的使用过程中到底应当选择哪种网络结构比较合适是值得考虑的。这就需要我们对各种神经网络结构有一个较全面的认识。

8. 神经网络应用。

直接用神经网络工具箱构建bp神经网络，希望能给个例子说明，有注解最好，本人matlab新手，谢谢 10

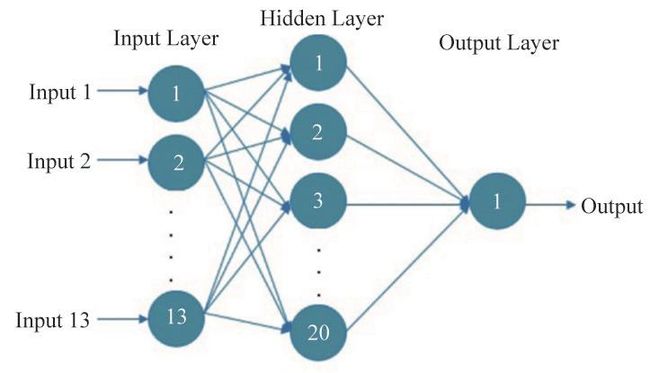
BP（Back Propagation）神经网络是1986年由Rumelhart和McCelland为首的科学家小组提出，是一种按误差逆传播算法训练的多层前馈网络，是目前应用最广泛的神经网络模型之一。BP网络能学习和存贮大量的输入-输出模式映射关系，而无需事前揭示描述这种映射关系的数学方程。它的学习规则是使用最速下降法，通过反向传播来不断调整网络的权值和阈值，使网络的误差平方和最小。BP神经网络模型拓扑结构包括输入层（input）、隐层(hidden layer)和输出层(output layer)。

附件就是利用神经网络工具箱构建BP神经网络进行预测的实例。如果要用可视化工具，可以在命令窗口输入nntool.。

有哪些深度神经网络模型？

目前经常使用的深度神经网络模型主要有卷积神经网络(CNN) 、递归神经网络(RNN)、深信度网络(DBN) 、深度自动编码器(AutoEncoder) 和生成对抗网络(GAN) 等。

递归神经网络实际.上包含了两种神经网络。一种是循环神经网络(Recurrent NeuralNetwork) ;另一种是结构递归神经网络(Recursive Neural Network)，它使用相似的网络结构递归形成更加复杂的深度网络。RNN它们都可以处理有序列的问题，比如时间序列等且RNN有“记忆”能力，可以“模拟”数据间的依赖关系。卷积网络的精髓就是适合处理结构化数据。

关于深度神经网络模型的相关学习，推荐CDA数据师的相关课程，课程以项目调动学员数据挖掘实用能力的场景式教学为主，在讲师设计的业务场景下由讲师不断提出业务问题，再由学员循序渐进思考并操作解决问题的过程中，帮助学员掌握真正过硬的解决业务问题的数据挖掘能力。这种教学方式能够引发学员的独立思考及主观能动性，学员掌握的技能知识可以快速转化为自身能够灵活应用的技能，在面对不同场景时能够自由发挥。点击预约免费试听课。