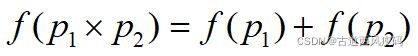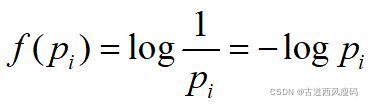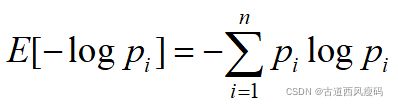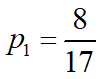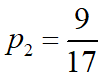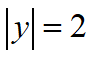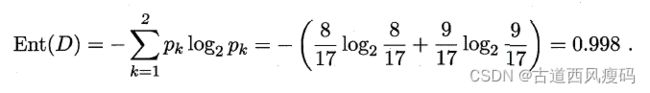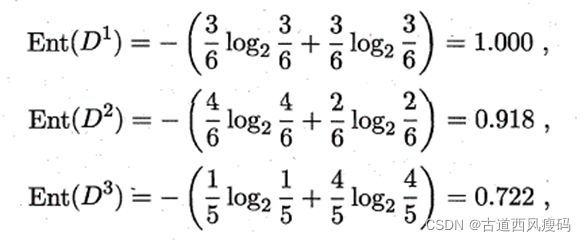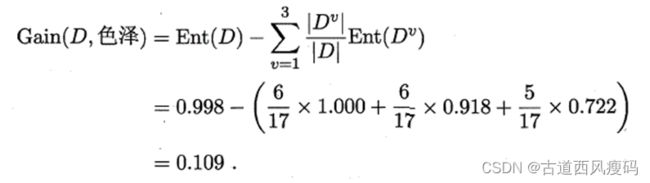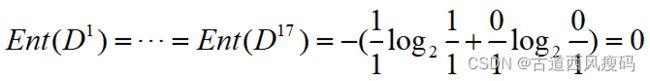决策树总结
根据训练数据是否拥有标记信息，可以把机器学习分为以下几类：
决策树（decision tree）模型常常用来解决分类和回归问题。常见的算法包括 CART (Classification And Regression Tree)、ID3、C4.5等。
二分类学习：
属性+属性值
决策树学习的目的：为了产生一颗泛化能力强的决策树，即处理未见示例能力强。
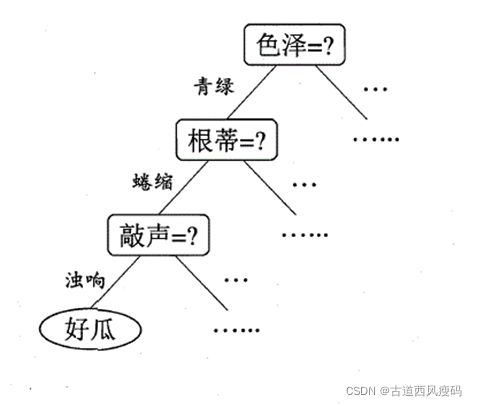
决策树学习的关键是算法的第8行：选择最优划分属性
什么样的划分属性是最优的？
我们希望决策树的分支结点所包含的样本尽可能属于同一类别，即结点的“纯度”越来越高，可以高效地从根结点到达叶结点，得到决策结果。
三种度量结点“纯度”的指标：
1. 信息增益
信息熵
香农提出了“信息熵”的概念，解决了对信息的量化度量问题。
香农用“信息熵”的概念来描述信源的不确定性。
假设我们已经知道衡量不确定性大小的这个量已经存在了，不妨就叫做“信息量”
同时满足这三个条件的函数f是负的对数函数，即
一个事件的信息量就是这个事件发生的概率的负对数。
信息熵是跟所有事件的可能性有关的，是平均而言发生一个事件得到的信息量大小。所以信息熵其实是信息量的期望。
信息增益
一般而言，信息增益越大，则意味着使用属性a来进行划分所获得的“纯度提升”越大。
决策树算法第8行选择属性
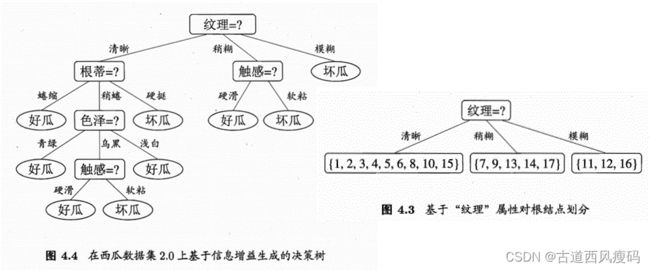
著名的ID3决策树算法
举例：求解划分根结点的最优划分属性
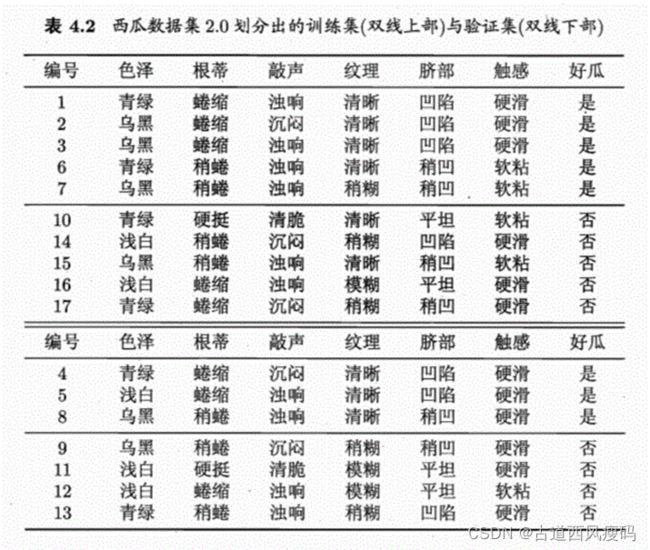
数据集包含17个训练样例：
8个正例（好瓜）占
9个反例（坏瓜）占
对于二分类任务
以属性“色泽”为例计算其信息增益
根结点的信息熵：
用“色泽”将根结点划分后获得3个分支结点的信息熵分别为：
属性“色泽”的信息增益为：
若把“编号”也作为一个候选划分属性，则属性“编号”的信息增益为：
根结点的信息熵仍为： 
用“编号”将根结点划分后获得17个分支结点的信息熵均为：
则“编号”的信息增益为：
远大于其他候选属性
信息增益准则对可取值数目较多的属性有所偏好
2. 增益率
增益率准则对可取值数目较少的属性有所偏好
著名的C4.5决策树算法综合了信息增益准则和信息率准则的特点：先从候选划分属性中找出信息增益高于平均水平的属性，再从中选择增益率最高的。
3. 基尼指数
基尼指数
著名的CART决策树算法
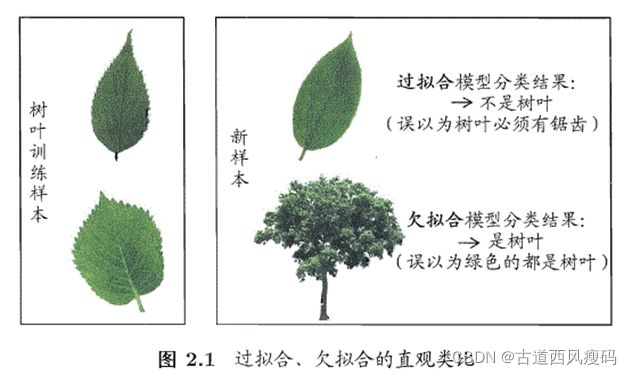
过拟合无法彻底避免，只能做到“缓解”。
剪枝，即通过主动去掉一些分支来降低过拟合的风险。
决策树的剪枝策略:预剪枝 / 后剪枝
预剪枝：在决策树生成过程中，对每个结点在划分前先进行估计，若当前结点的划分不能带来决策树泛化性能提升，则停止划分并将当前结点标记为叶结点
后剪枝：先从训练集生成一棵完整的决策树，然后自底向上地对非叶结点进行考察，若将该结点对应的子树替换为叶结点能带来决策树泛化性能提升，则将该子树替换为叶结点。
留出法：将数据集D划分为两个互斥的集合：训练集S和测试集T
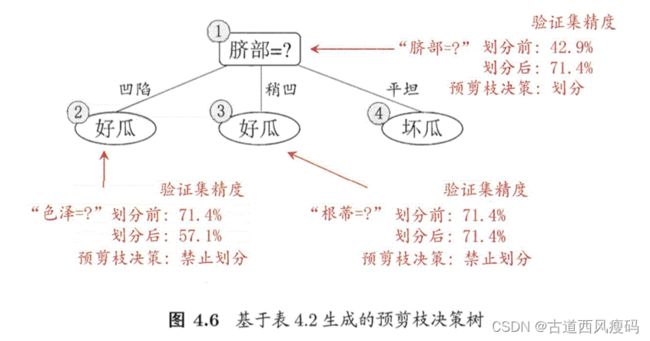
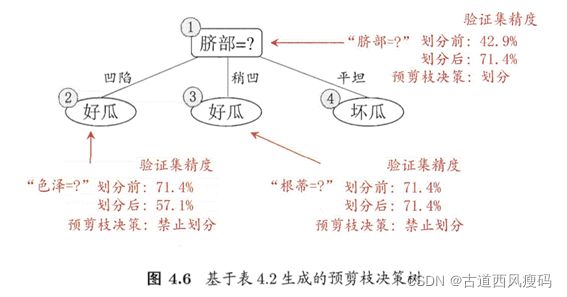
预剪枝
精度：正确分类的样本占所有样本的比例,
训练集：好瓜 坏瓜1,2,3,6,7,10,14,15,16,17
验证集：4,5,8,9,11,12,13
预剪枝使得决策树的很多分支都没有“展开”
优点：
不足：
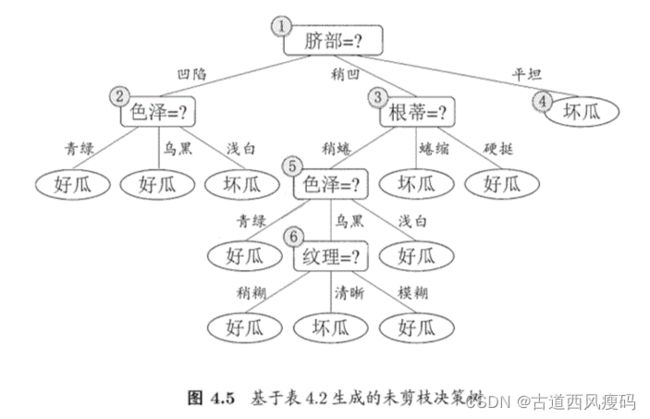
后剪枝
先从训练集生成一棵完整的决策树，然后自底向上地对非叶结点进行考察，若将该结点对应的子树替换为叶结点能带来决策树泛化性能提升，则将该子树替换为叶结点。
训练集：好瓜 坏瓜1,2,3,6,7,10,14,15,16,17
验证集：4,5,8,9,11,12
后剪枝决策树
预剪枝决策树
