近端策略优化理解记录

---

前言

Proximal Policy Optimization（PPO）即近端策略优化，是Policy Graident的一种改进算法，属于Importce Sampling的方法，将Policy Gradient中On-policy的训练过程转化为Off-policy。

---

一、梯度下降？

1 梯度

可以简单理解为一个多元函数在空间的某个点上最大方向导数的矢量，梯度的本意是一个向量（矢量），表示某一函数在该点处的方向导数沿着该方向取得最大值，即函数在该点处沿着该方向（此梯度的方向）变化最快，变化率最大（为该梯度的模）。 $$f\left(x,y\right)$$ 的梯度为$$\left(f_x,f_y\right)$$ ，给定具体的点（X,Y)则可以计算出$$\left(f_X,f_Y\right)$$ ，该梯度为一个向量，若是一元函数则在给定坐标后，梯度为一个数值。
比如：$$z=f\left(x,y\right)=x^2-y^2$$ 函数图像为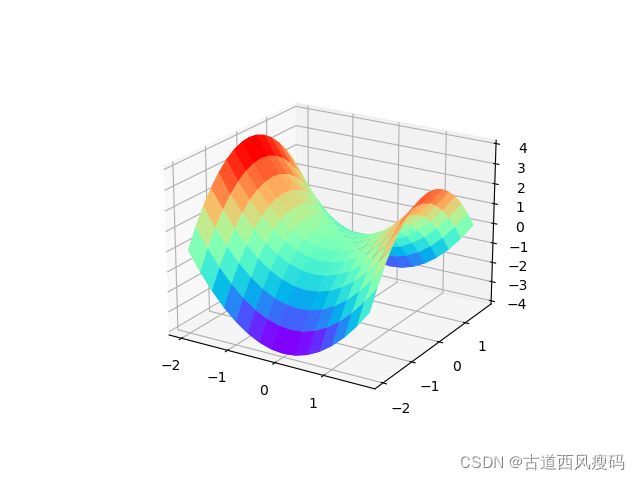
其梯度为$$\left(2x,-2y\right)$$ 在坐标轴上的图像为

2 梯度下降

二、Proximal Policy Optimization （PPO）

1.策略梯度

Policy Gradient基于策略迭代，直接通过采样状态、动作、奖励，然后最大化奖励的期望。
当采样足够充分时，奖励的期望可以近似为N回合的奖励的平均值：$${\bar{R}}_{\theta }=\sum _{\tau }R\left(\tau \right)P\left(\tau |\theta \right)\approx \frac{1}{N}\sum _{n=1}^{N}R\left({\tau }^n\right)$$
策略梯度：设计一个网络，其输入是state，输出是对应各个action的概率，并策略梯度（PolicyGradient）进行迭代训练。定义一个回合为：$$\tau =s_1,a_1,r_1,\cdots ,s_T,a_T,r_T$$
其中$$R\left(\tau \right)=\sum _{t=1}^T{r}_t$$ 对R平均求梯度$$\nabla {\bar{R}}_{\theta }=\sum _{\tau }R\left(\tau \right)\nabla P\left(\tau |\theta \right)$$ $$=\sum _{\tau }R\left(\tau \right)P\left(\tau |\theta \right)\cdot \frac{\nabla P\left(\tau |\theta \right)}{P\left(\tau |\theta \right)}$$ $$=\sum _{\tau }R\left(\tau \right)P\left(\tau |\theta \right)\cdot \nabla \log P\left(\tau |\theta \right)$$ $$=\frac{1}{N}\sum _{n=1}^{N}R\left({\tau }^n\right)\cdot \nabla \log P\left({\tau }^n|\theta \right)$$
其中P可以写为$$P\left({\tau }^n|\theta \right)=P\left(s_1\right)P\left(a_1|s_1,\theta \right)P\left(r_1,s_2|s_1,a_1\right)P\left(a_2|s_2,\theta \right)\cdots P\left(a_t|s_t,\theta \right)P\left(r_t,s_{t+1}|s_t,a_t\right)$$ $$=P\left(s_1\right)\prod _{t}P\left(a_t|s_t,\theta \right)P\left(r_t,s_{t+1}|s_t,a_t\right)$$ 代入前式中，
$$\nabla \log p\left({\tau }^n|\theta \right)=\nabla \log \left(p\left(s_1\right)\prod _{t}p\left(a_t|s_t,\theta \right)p\left(r_t,s_{t+1}|s_t,a_t\right)\right)$$ $$=\nabla \log p\left(s_1\right)+\sum _{t=1}^T\nabla \log p\left(a_t|s_t,\theta \right)+\sum _{t=1}^T\nabla p\left(r_t,s_{t+1}|s_t,a_t\right)$$ $$=\sum _{t=1}^T\nabla \log p\left(a_t|s_t,\theta \right)$$
随即
$$\nabla {\bar{R}}_{\theta }=\frac{1}{N}\sum _{n=1}^N\sum _{t=1}^{T_n}R\left({\tau }^n\right)\nabla \log p\left(a_t|s_t,\theta \right)$$
最小化N回合采样出的action与网络输出的action交叉熵基础上乘以R，即
$$-\sum _{n=1}^{N}R\left({\tau }^n\right)\cdot a_i\log p_i$$
交叉熵公式为
$$H_p\left(q\right)=\sum _{x}q\left(x\right){\log }_2\left(\frac{1}{p\left(x\right)}\right)=-\sum _{x}q\left(x\right){\log }_{2}p\left(x\right)$$

2.Actor-Critic Model

这个改进针对每一个状态、动作元组对进行替换$$R\left({\tau }^n\right)\to \sum _{t=t^{\prime }}^{T_n}{\gamma }^{t-t^{\prime }}{r}_t^n$$ 梯度公式将会被改写为
$$\nabla {\bar{R}}_{\theta }=\frac{1}{N}\sum _{n=1}^N\sum _{t=1}^{T_n}\sum _{t=t^{\prime }}^{T_n}{\gamma }^{t-t^{\prime }}{r}_t^n\nabla \log p\left(a_t|s_t,\theta \right)$$
此时还存在过估计（Overestimate）问题，因为有些状态-动作采样不到，而另一些则反复采样。这样当输出softmax后，选择概率差距被进一步放大，则需要进行下一个改进。
（1）Baseline：常超参数
（2）Critic网络
Actor-Critic Model：
$$\nabla {\bar{R}}_{\theta }=\frac{1}{N}\sum _{n=1}^N\sum _{t=1}^{T_n}{A}^{\theta }\left(a_t|s_t\right)\nabla \log p\left(a_t|s_t,\theta \right)$$

The value of the advantage function represents the additional gain brought by taking action a.

3 Import sampling

上面的梯度$$\nabla {\bar{R}}_{\theta }$$表明采样的轨迹为参数θ的功劳，但是当更新了参数后，新的参数下概率也会发生变化，即状态-动作对的分布发生了变化，原先的样本也就不能用了。也就是说同样的策略不能一边采样一边更新，一个解决办法就是采取异策略，这么做的好处是一个策略采集到的样本可以被反复使用，梯度上升多次。具体的做法就是importance sampling。
假设一个连续随机变量X概率密度为p(x)，函数f(x)的期望可以表示为$$E_{x-p}\left[f\left(x\right)\right]=\int f\left(x\right)p\left(x\right)dx$$ 设另一个概率密度函数为q(x)，则对于上述函数期望也可以写为
$$E_{x-p}\left[f\left(x\right)\right]=\int f\left(x\right)\cdot p\left(x\right)dx$$ $$=\int f\left(x\right)\cdot \frac{p\left(x\right)}{q\left(x\right)}q\left(x\right)dx$$ $$=E_{x-q}\left[f\left(x\right)\frac{p\left(x\right)}{q\left(x\right)}\right]$$
其中p(x)/q(x)称为importance weight，类比问题将f(x)当作A(at|st)，而p(x)/q(x)为两种策略对于当前状态采取当前动作对应概率之比。
假如采样足够充分的话，可以认为：
$$E_{x-p}\left[f\left(x\right)\right]=E_{x-q}\left[f\left(x\right)\frac{p\left(x\right)}{q\left(x\right)}\right]$$

3 PPO

Importance sampling将On-policy转化为Off-policy，在利用q(x)充分采样的情况下更新p(x)，这个过程可以在一回合重复N次，而不再是1次，这样大幅度减少了原始PG算法在线学习进行采样状态-动作-奖励元组对时间，同时保证了训练效果。
$$\nabla {\bar{R}}_{\theta }=\frac{1}{N}\sum _{n=1}^N\sum _{t=1}^{T_n}\frac{p_{\theta }\left(a_t|s_t\right)}{p_{{\theta }^{\prime }}\left(a_t{s}_t\right)}{A}^{\theta }\left(a_t|s_t\right)\nabla \log p\left(a_t|s_t,\theta \right)$$
其中$$\frac{p_{\theta }\left(a_t|s_t\right)}{p_{{\theta }^{\prime }}\left(a_t{s}_t\right)}$$有时进行修正操作，如Clipped，将比值限制在（1-ε，1+ε）内。

令$$r_t\left(\theta \right)=\frac{{\pi }_{\theta }\left(a_t|s_t\right)}{{\pi }_{{\theta }_{old}}\left(a_t|s_t\right)}$$

$$L^{clip}\left(\theta \right)={\hat{E}}_t\left[\min \left(r_t\left(\theta \right)A_t,clip\left(r_t\left(\theta \right),1-ϵ,1+ϵ\right){\hat{A}}_t\right)\right]$$

其中，ε为超参数一般设置为0.2，然后对Lclip进行SGD优化。
$${\hat{A}}_t>0$$ 为优势函数，其＞0时表示策略更好，应该进一步优化，当

---

总结

控制新旧策略的比值$$r_t\left(\theta \right)$$
防止更新影响agent学习效果。