装载问题-分支限界法(队列式分支限界法,优先队列式分支限界法)
问题描述
有n个集装箱要装上2艘载重量分别为c1和c2的轮船,其中集装箱i的重量为wi,且
∑ i = 1 n w i ≤ c 1 + c 2 \sum^n_{i=1}w_i≤c_1+c_2 i=1∑nwi≤c1+c2
问题:
是否有一个合理的装载方案,可将这n个集装箱装上这2艘轮船?如果有,找出一种装载方案。
例如:当n=3, c1=c2=50
(1)若w=[10, 40, 40]
可将集装箱1和集装箱2装上第一艘轮船,而将集装箱3装上第二艘轮船;
(2)如果w=[20, 40, 40]
则无法将这3个集装箱都装上船;
基本思路
已证明,如果一个给定装载问题有解,则采用下面的策略可得到最优装载方案。
- 首先将第一艘轮船尽可能装满;
- 将剩余的集装箱装上第二艘轮船。
将第一艘轮船尽可能装满等价于选取全体集装箱的一个子集,使该子集中集装箱重量之和最接近c1。由此可知,装载问题等价于以下特殊的0-1背包问题。
队列式分支限界法
- 解装载问题的队列式分支限界法
仅求出所要求的最优值,稍后进一步构造最优解。 - 首先检测当前扩展结点的左儿子结点是否为可行结点。如果是,则将其加入到活结点队列Q中。
- 然后,将其右儿子结点加入到活结点队列中(右儿子结点一定是可行结点)。2个儿子结点都产生后,当前扩展结点被舍弃。
- 活结点队列中,队首元素被取出作为当前扩展结点。
- 活结点队列已空,算法终止。
例子
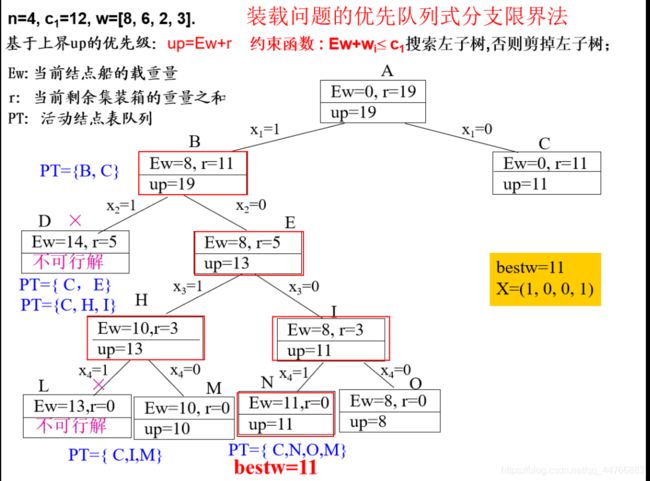
例如 n=4, c1=12, w=[8, 6, 2, 3].
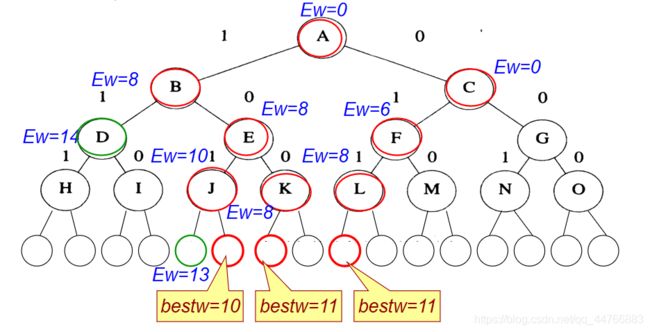
注:叶子结点不会被扩展,因此不用加入到活结点队列当中,此时,只需要检查该叶节点表示的最优解是否优于当前最优解,并实时更新当前最优解。
同层尾部标记:-1
活结点队列:
当取出的元素是-1时,判断当前队列是否为空,如果队列不空,则将尾部标记 -1加入到活节点队列中,代表算法开始处理下一层活节点,即:代表算法开始处理 下一个物品的装载问题(每一层i开始处理第i个物品的装载)。
代码(伪代码)
emplate
Type MaxLoading(Type w[], Type c, int n)
{ //初始化
QueueQ; // 活结点队列
Q.Add(-1); // 同层结点尾部标志
int i=1; //当前扩展结点所处的层
Type Ew=0; //扩展结点处相应的载重量
bestw=0;
//搜索子集空间树
while (true) {
// 检查左儿子结点
if (Ew + w[i] <= c1) // x[i] = 1,Ew存储当前扩展结点相应的载重量
EnQueue(Q, Ew + w[i], bestw, i, n); //将活结点加入到活结点队列Q中
// 右儿子结点总是可行的,将其加入到Q中
EnQueue(Q, Ew, bestw, i, n); // x[i] = 0
Q.Delete(Ew); // 取下一扩展结点
if (Ew == -1) { // 同层结点尾部
if (Q.IsEmpty( )) return bestw;
Q.Add(-1); // 同层结点尾部标志
Q.Delete(Ew); // 取下一扩展结点
i++;} // 进入下一层
}
}
算法的改进
算法MaxLoading初始时bestw=0,直到搜索到第一个叶结点才更新bestw。在搜索到第一个
叶结点前,总有Ew+r>bestw, 此时右子树测试不起作用。
为确保右子树成功剪枝,应该在算法每一次进入左子树的时候更新bestw的值。
样例
分析演示
代码改进(伪代码)
while (true) {
// 检查左儿子结点
// wt=Ew + w[i]; // 左儿子结点的重量
if (wt<= c) { // 可行结点
if (wt > bestw) bestw = wt; //提前更新bestW,注意更新条件
// 加入活结点队列
if (i <= n) Q.Add(wt);
}
// 检查右儿子结点
if (Ew + r > bestw && i <= n) //右儿子剪枝
Q.Add(Ew); // 可能含最优解
Q.Delete(Ew); // 取下一扩展结点
if (Ew == -1) { // 同层结点尾部
if (Q.IsEmpty()) return bestw;
Q.Add(-1); // 同层结点尾部标志
Q.Delete(Ew); // 取下一扩展结点
i++;
r-=w[i];} // 进入下一层
}
}
代码
#include
using namespace std;
typedef struct QNode
{
QNode *parent;
int lchild;
int weight;
}QNode;
int n;
int c;
int bestw;
int w[100];
int bestx[100];
void InPut()
{
scanf("%d %d", &n, &c);
for(int i = 1; i <= n; ++i)
scanf("%d", &w[i]);
// for(int i = 1; i <= n; ++i)
// printf("%d ", w[i]);
// cout << endl;
// printf("输入结束\n");
}
//QNode *&bestE 的原因是 首先bestE是个地址, 其次引用为了赋值使用, 后边for循环中用到
void EnQueue(queue &q, int wt, int i, QNode *E, QNode *&bestE, int ch)
{
if(i == n)
{
if(wt == bestw)
{
bestE = E;
bestx[n] = ch;
return;
}
}
QNode *b;
b = new QNode;
b->weight = wt;
b->lchild = ch;
b->parent = E;
q.push(b);
}
int MaxLoading()
{
queueq;
q.push(0);
int i = 1;
int Ew = 0, r = 0;
bestw = 0;
for(int j = 2; j <= n; ++j)
r += w[j];
QNode *E, *bestE; //bestE的作用是:结束while循环后,bestE指向最优解的叶子节点,然后通过bestE->parent找到装入了哪些物品。
E = new QNode; //E这里作为一个中间量,连接parent和child
E = 0; //赋0是因为树的根的值是0,while刚开始的时候其代表root
while(true)
{
int wt = Ew + w[i];
if(wt <= c)
{
if(wt > bestw) //提前更新bestW,注意更新条件
bestw = wt;
EnQueue(q, wt, i, E, bestE, 1);
}
if(Ew + r >= bestw) //右儿子剪枝
{
EnQueue(q, Ew, i, E, bestE, 0);
}
E = q.front();
q.pop();
if(!E) //如果取得的数是0,代表该处理下一层
{
if(q.empty()) //如果队列为空,表示该循环结束了
break;
q.push(0); //如果队列中还有数据,表示循环还没结束。在该层的末尾加一个0标识符
E = q.front();
q.pop();
i++; //下一层走起
r -= w[i]; //计算剩余的重量
}
Ew = E->weight; //不要忘记更新最新节点的值
}
for(int j = n - 1; j > 0; --j)
{
bestx[j] = bestE->lchild;
bestE = bestE->parent;
}
}
void OutPut()
{
printf("最优装载量为 %d\n", bestw);
printf("装载的物品为 \n");
for(int i = 1; i <= n; ++i)
if(bestx[i] == 1)
printf("%d ", i);
}
int main()
{
InPut();
MaxLoading();
OutPut();
}
样例测试
数据为上面那个样例
输入
4 12
8 6 2 3
输出
最优装载量为 11
装载的物品为
1 4
优先队列式分支限界法
- 解装载问题的优先队列式分支限界法用最大优先队列存储活结点表。
- 活结点x在优先队列中的优先级定义为从根结点到结点x的路径所相应的载重量Ew(即:当前扩展结点船的载重量Ew)再加上剩余集装箱的重量r之和(即:将上界Ew+r定义为结点优先级)。
- 优先队列中优先级最大的活结点成为下一个扩展结点。
- 子集树中叶结点所相应的载重量与其优先级(上界值)相同,即:该叶子结点的上界值等于当前叶子结点处船的重量Ew。
- 在优先队列式分支限界法中,一旦有一个叶结点成为当前扩展结点,则可以断言该叶结点所相应的解即为最优解。此时可终止算法。
求最优解
- 在优先队列的每一个活结点中,保存从解空间树的根结点到该活结点的路径,在算法确定了达到最优值的叶结点时,就在该叶结点处同时得到相应的最优解。
- 在算法的搜索进程中,保存当前已构造出的部分解空间树,这样在算法确定了达到最优值的叶结点时,可以在解空间树中从该叶结点开始向根结点回溯,构造出相应的最优解。
样例
分析演示
代码
#include
using namespace std;
class MaxHeapQNode
{
public:
MaxHeapQNode *parent; //父节点
int lchild; //左节点:1; 右节点"0
int weight; //总重量
int lev; //层次
};
struct cmp
{
bool operator()(MaxHeapQNode *&a, MaxHeapQNode *&b) const
{
return a->weight < b->weight;
}
};
int n;
int c;
int bestw;
int w[100];
int bestx[100];
void InPut()
{
scanf("%d %d", &n, &c);
for(int i = 1; i <= n; ++i)
scanf("%d", &w[i]);
}
void AddAliveNode(priority_queue, cmp> &q, MaxHeapQNode *E, int wt, int i, int ch)
{
MaxHeapQNode *p = new MaxHeapQNode;
p->parent = E;
p->lchild = ch;
p->weight = wt;
p->lev = i + 1;
q.push(p);
}
void MaxLoading()
{
priority_queue, cmp > q; // 大顶堆
//定义剩余重量数组r
int r[n + 1];
r[n] = 0;
for(int j = n - 1; j > 0; --j)
r[j] = r[j + 1] + w[j + 1];
int i = 1;
MaxHeapQNode *E;
int Ew = 0;
while(i != n + 1)
{
if(Ew + w[i] <= c)
{
AddAliveNode(q, E, Ew + w[i] + r[i], i, 1);
}
AddAliveNode(q, E, Ew + r[i], i, 0);
//取下一节点
E = q.top();
q.pop();
i = E->lev;
Ew = E->weight - r[i - 1];
}
bestw = Ew;
for(int j = n; j > 0; --j)
{
bestx[j] = E->lchild;
E = E->parent;
}
}
void OutPut()
{
printf("最优装载量为 %d\n", bestw);
printf("装载的物品为 \n");
for(int i = 1; i <= n; ++i)
if(bestx[i] == 1)
printf("%d ", i);
}
int main()
{
InPut();
MaxLoading();
OutPut();
}
样例测试
数据为上面那个样例
输入
4 12
8 6 2 3