回归预测 | MATLAB实现GWO-LSTM灰狼算法优化长短期记忆神经网络多输入单输出回归预测

回归预测 | MATLAB实现GWO-LSTM灰狼算法优化长短期记忆神经网络多输入单输出回归预测

预测效果

基本介绍

MATLAB实现GWO-LSTM灰狼算法优化长短期记忆网络多输入单输出。优化参数为学习率，隐藏层节点个数，正则化参数。

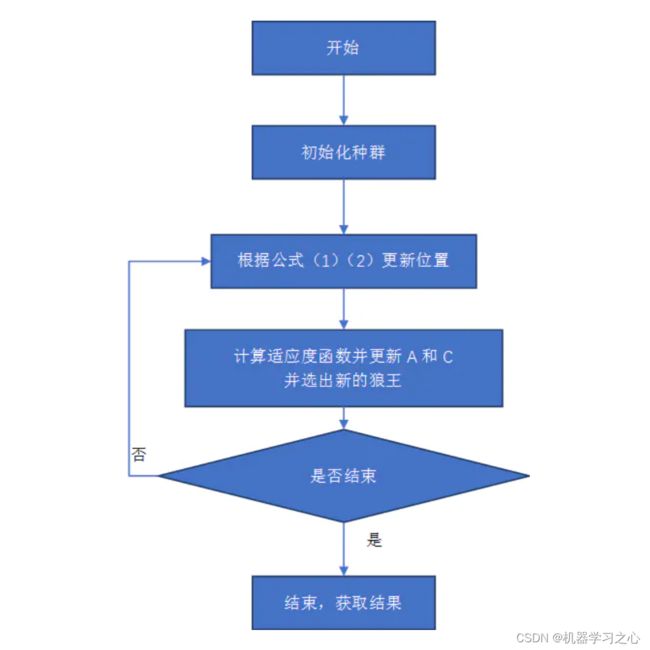
模型描述

• 灰狼优化算法（Grey Wolf Optimizer，GWO）由澳大利亚格里菲斯大学学者 Mirjalili 等人于2014年提出来的一种群智能优化算法。该算法受到了灰狼捕食猎物活动的启发而开发的一种优化搜索方法，它具有较强的收敛性能、参数少、易实现等特点。

• GWO算法的主要缺点是处理大量变量的能力和在解决大规模问题时逃避局部解的能力。混合GWO和其他当前的算法可以设计各种模型算法。通过使用其他算法的运算符，可以改进对GWO的探索和利用。
• GWO将群体分成四组，这被证明是解决基准问题的有效机制。在解决具有挑战性的现实问题时，考虑或多或少拥有不同数量狼的分组可以被视为一个研究领域，提高GWO的性能。
• 长短期记忆（Long short-term memory, LSTM）是一种特殊的RNN，主要是为了解决长序列训练过程中的梯度消失和梯度爆炸问题。简单来说，就是相比普通的RNN，LSTM能够在更长的序列中有更好的表现。

程序设计

• 完整程序和数据下载方式1(资源处直接下载)：MATLAB实现GWO-LSTM灰狼算法优化长短期记忆网络多输入单输出
• 完整程序和数据下载方式2(订阅《智能学习》专栏，同时获取《智能学习》专栏收录程序6份，数据订阅后私信我获取)：MATLAB实现GWO-LSTM灰狼算法优化长短期记忆网络多输入单输出

%%  清空环境变量
warning off             % 关闭报警信息
close all               % 关闭开启的图窗
clear                   % 清空变量
clc                     % 清空命令行
tic
% restoredefaultpath
f_=size(P_train, 1);                  % 输入特征维度
outdim = 1;                           % 最后一列为输出

%%  数据归一化
[p_train, ps_input] = mapminmax(P_train, 0, 1);
p_test = mapminmax('apply', P_test, ps_input);

[t_train, ps_output] = mapminmax(T_train, 0, 1);
t_test = mapminmax('apply', T_test, ps_output);
%%  划分训练集和测试集
M = size(P_train, 2);
N = size(P_test, 2);

%%  优化算法参数设置
SearchAgents_no = 5;                   % 狼群数量
Max_iteration = 15;                    % 最大迭代次数
dim = 3;                               % 优化参数个数
lb = [1e-3, 10, 1e-4];                 % 参数取值下界(学习率，隐藏层节点，正则化系数)
ub = [1e-2, 30, 1e-1];                 % 参数取值上界(学习率，隐藏层节点，正则化系数)

%%  优化算法初始化
Alpha_pos = zeros(1, dim);  % 初始化Alpha狼的位置
Alpha_score = inf;          % 初始化Alpha狼的目标函数值,将其更改为-inf以解决最大化问题

Beta_pos = zeros(1, dim);   % 初始化Beta狼的位置
Beta_score = inf;           % 初始化Beta狼的目标函数值 ,将其更改为-inf以解决最大化问题

Delta_pos = zeros(1, dim);  % 初始化Delta狼的位置
Delta_score = inf;          % 初始化Delta狼的目标函数值,将其更改为-inf以解决最大化问题

%%  初始化搜索狼群的位置
Positions = initialization(SearchAgents_no, dim, ub, lb);

%%  用于记录迭代曲线
Convergence_curve = zeros(1, Max_iteration);

%%  循环计数器
iter = 0;

%%  优化算法主循环
while iter < Max_iteration           % 对迭代次数循环
    for i = 1 : size(Positions, 1)   % 遍历每个狼

        % 返回超出搜索空间边界的搜索狼群
        % 若搜索位置超过了搜索空间，需要重新回到搜索空间
        Flag4ub = Positions(i, :) > ub;
        Flag4lb = Positions(i, :) < lb;

        % 若狼的位置在最大值和最小值之间，则位置不需要调整，若超出最大值，最回到最大值边界
        % 若超出最小值，最回答最小值边界
        Positions(i, :) = (Positions(i, :) .* (~(Flag4ub + Flag4lb))) + ub .* Flag4ub + lb .* Flag4lb;   

        % 计算适应度函数值
        Positions(i, 2) = round(Positions(i, 2));
        fitness = fical(Positions(i, :));

        % 更新 Alpha, Beta, Delta
        if fitness < Alpha_score           % 如果目标函数值小于Alpha狼的目标函数值
            Alpha_score = fitness;         % 则将Alpha狼的目标函数值更新为最优目标函数值
            Alpha_pos = Positions(i, :);   % 同时将Alpha狼的位置更新为最优位置
        end

        if fitness > Alpha_score && fitness > Beta_score && fitness < Delta_score  % 如果目标函数值介于于Beta狼和Delta狼的目标函数值之间
            Delta_score = fitness;                                                 % 则将Delta狼的目标函数值更新为最优目标函数值
            Delta_pos = Positions(i, :);                                           % 同时更新Delta狼的位置
        end

    end

    % 线性权重递减
    wa = 2 - iter * ((2) / Max_iteration);    

    % 更新搜索狼群的位置
    for i = 1 : size(Positions, 1)      % 遍历每个狼
        for j = 1 : size(Positions, 2)  % 遍历每个维度

            % 包围猎物，位置更新
            r1 = rand; % r1 is a random number in [0,1]
            r2 = rand; % r2 is a random number in [0,1]

            A1 = 2 * wa * r1 - wa;   % 计算系数A，Equation (3.3)
            C1 = 2 * r2;             % 计算系数C，Equation (3.4)

            % Alpha 位置更新
            D_alpha = abs(C1 * Alpha_pos(j) - Positions(i, j));   % Equation (3.5)-part 1
            X1 = Alpha_pos(j) - A1 * D_alpha;                     % Equation (3.6)-part 1

            r1 = rand; % r1 is a random number in [0,1]
            r2 = rand; % r2 is a random number in [0,1]

            A2 = 2 * wa * r1 - wa;   % 计算系数A，Equation (3.3)
            C2 = 2 *r2;              % 计算系数C，Equation (3.4)

            % Beta 位置更新
            D_beta = abs(C2 * Beta_pos(j) - Positions(i, j));    % Equation (3.5)-part 2
            X2 = Beta_pos(j) - A2 * D_beta;                      % Equation (3.6)-part 2       

            r1 = rand;  % r1 is a random number in [0,1]
            r2 = rand;  % r2 is a random number in [0,1]

            A3 = 2 *wa * r1 - wa;     % 计算系数A，Equation (3.3)
            C3 = 2 *r2;               % 计算系数C，Equation (3.4)

            % Delta 位置更新
            D_delta = abs(C3 * Delta_pos(j) - Positions(i, j));   % Equation (3.5)-part 3
            X3 = Delta_pos(j) - A3 * D_delta;                     % Equation (3.5)-part 3

            % 位置更新
            Positions(i, j) = (X1 + X2 + X3) / 3;                 % Equation (3.7)

        end
    end

    % 更新迭代器
    iter = iter + 1;   
    disp(['第',num2str(iter),'次迭代'])
    Convergence_curve(iter) = Alpha_score;

end

参考资料

[1] https://blog.csdn.net/article/details/126072792spm=1001.2014.3001.5502
[2] https://blog.csdn.net/article/details/126044265spm=1001.2014.3001.5502