【论文阅读笔记】Network Sketching: Exploiting Binary Structure in Deep CNNs
全文概括
草图,就像在画画一样,是不断精确的基础,在二进制量化的应用上,即不断地逼近残差,如 HORQ (High-Order Residual Quantization) 一样。与 HORO 的区别在于,该方向并未二值化 Input,但其提出了一个新的 尺度因子的计算方式。
在 2-bit/ 1-bit 的极低精度的近似 ResNet-18 的结果展示上,其与 INQ 的精确度差不多,但多了几层的二值化卷积,即时间效率下降。【本文提供了一种 Associative Implementation 的方式来解决而这个问题】
提供了一种二值权重共享卷积计算的方式,即Associative Implementation,其计算方式直观上就是:在同一层卷积(即输入 X X X是同一个,而卷积核不同),保留上一次的卷积结果,对于卷积核一样的部分不进行计算,只计算卷积核不同的部分。
Network Sketching

对每一个 W ∈ R c ∗ w ∗ h W \in \mathcal{R}^{c*w*h} W∈Rc∗w∗h 都有 m m m 个 B ∈ R c ∗ w ∗ h B \in \mathcal{R}^{c*w*h} B∈Rc∗w∗h 的二进制 Tensor ,和 m m m 个 对应的尺度因子。
对于文中的两种 Sketching 方法,不同的地方只在于 尺度因子 的计算。
Direct Approximation
B j = s g n ( W j ^ ) B_j = sgn(\hat{W_j}) Bj=sgn(Wj^) a j = < B j , W j ^ > t a_j=\frac{<B_j,\hat{W_j}>}t aj=t<Bj,Wj^> 其中, W j ^ \hat{W_j} Wj^是前面量化的残差,初始化 W 0 ^ = W \hat{W_0} = W W0^=W; t = c ∗ w ∗ h t = c*w*h t=c∗w∗h,是该层该 filter 参数的个数。
该方法和 HORQ 一模一样
Approximation with Refinement
由于上面的方法,在逼近残差时,其收敛程度低,收敛速度慢(逼近原始权重 Tensor 的程度),因此提出了新的尺度因子计算方式,使得能更加逼近原始权重: a j = ( B j T B j ) − 1 B j T ∗ v e c ( W ) a_j = (B_j^TB_j)^{-1}B_j^T*vec(W) aj=(BjTBj)−1BjT∗vec(W) 其中, v e c ( ∗ ) vec(*) vec(∗) 是其输入的一个列向量,比如 B j = [ v e c ( B 0 ) , . . . , v e c ( B j ) ] B_j = [vec(B_0),...,vec(B_j)] Bj=[vec(B0),...,vec(Bj)]
其目的是想利用 W W W 的整体信息,即先前的量化逼近结果 B i B_i Bi 也利用上。
Speeding-up the Sketch Model
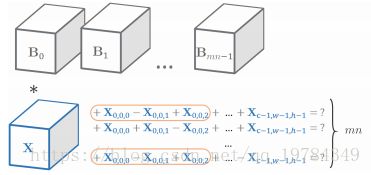
对于一个输入 Tensor X X X,如果有多个 B B B 与其卷积,则其可能和之前的卷积操作计算有重叠的部分,则我们进行 B j B_j Bj 卷积时,可以利用 B j − 1 B_{j-1} Bj−1 的卷积计算结果。
Associative Implementation
假设 X 和 B j 0 X 和 B_{j_0} X和Bj0的计算结果已经得出: X ⊗ B j 0 = s X \otimes B_{j_0}=s X⊗Bj0=s,则我们有: (1) X ⊗ B j 1 = s + ( X ⊗ ( B j 0 ∨ B j 1 ) ) ∗ 2 X \otimes B_{j_1} = s + (X \otimes (B_{j_0} \vee B_{j_1})) * 2 \tag{1} X⊗Bj1=s+(X⊗(Bj0∨Bj1))∗2(1) (2) X ⊗ B j 1 = s − ( X ⊗ ( ¬ B j 0 ∨ B j 1 ) ) ∗ 2 X \otimes B_{j_1} = s - (X \otimes ( \neg B_{j_0} \vee B_{j_1})) * 2 \tag{2} X⊗Bj1=s−(X⊗(¬Bj0∨Bj1))∗2(2)
| B J 1 B_{J_1} BJ1 | B j 2 B_{j_2} Bj2 | B J 1 ∨ B j 2 B_{J_1} \vee B_{j_2} BJ1∨Bj2 |
|---|---|---|
| +1 | -1 | -1 |
| +1 | +1 | 0 |
| -1 | -1 | 0 |
| -1 | +1 | +1 |
关联计算的规则如上,直观上来看,就是和上一个卷积核一样的部分,就利用上一次的结算结果,和上一次不一样的部分,才需要计算(在这里就是不一样的部分,就用上一次的卷积结果的基础上,加上两倍的不一样地方)。
假设 B j 0 ∨ B j 1 B_{j_0} \vee B_{j_1} Bj0∨Bj1 的内积结果为 r ∈ [ − t , + t ] r \in [-t, +t] r∈[−t,+t]。我们有以下结果:公式 ( 1 ) (1) (1)和公式 ( 2 ) (2) (2)需要的计算量不同,公式 ( 1 ) (1) (1)为 t − r 2 \frac{t-r}{2} 2t−r,公式 ( 2 ) (2) (2)为 t + r 2 \frac{t+r}2 2t+r 。所以有:当 r > 0 r > 0 r>0,使用公式 ( 1 ) (1) (1);当 r < 0 r < 0 r<0,使用公式 ( 2 ) (2) (2)。
该二值权重卷积计算共享的方法可以运用于任意的树上,但如果使用最小生成树得到最优的共享计算方式,可以进一步优化算法。【该部分在 4.2 Constructing a Dependency Tree 上】
结果展示
原始的 AlexNet 的参数数量 和 计算数量 :

Refined-Sketch的结果:

在这两层中,参数少了 10 x 10x 10x 倍,FMUL(浮点数乘法运算)少了 400 x 400x 400x 到 3000 x 3000x 3000x 倍。【这里乘法操作少了,但加法操作会增加】
Associative Implementation 的结果:就是 FADDs 的减少
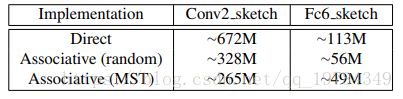
在这两层中,使用基于最小生成树的 Associative Implementation 可以减少 2.5 2.5 2.5 倍和 2.3 2.3 2.3 倍的加法操作。

