论文阅读笔记(2):Learning a Self-Expressive Network for Subspace Clustering,SENet,用于大规模子空间聚类的自表达网络
论文阅读笔记(2):Learning a Self-Expressive Network for Subspace Clustering. SENet——用于大规模子空间聚类的自表达网络
- 前言
- 摘要
- 一、简介
- 二、相关工作
-
- 深度聚类
- 自表达模型
- 可伸缩子空间聚类
- 自注意力模型
- 三、自表达网络 SENet
-
- 3.1 模型
-
- 正则化项的选择
- 3.2 网络实例化
-
- 与自注意力机制的比较
- 3.3 训练
-
- 双道算法
- 四、实验
-
-
- 网络架构
- 矩阵
- 4.1 在人工数据上的实验
-
- 自表达系数的可视化
- 将SENet于EnSC相比较
- 4.2 在真实数据集上的实验
-
- SENet的泛化性能
- SENet在大型数据集上
-
- 附录
-
- 合成数据集上的结果
- 真实数据集上的结果(一下都以CIFAR-10为例)
-
- Soft-Thresholding的作用
- 模型设计和训练参数选择
前言
是今年本组的CVPR论文,拜读一下并留档。
摘要
最先进的子空间聚类方法是基于自表达模型的方法,将每个数据点表示为其他数据点的线性组合。然而,这种方法是为有限样本数据集设计的,缺乏推广到样本外数据的能力。此外,由于自表达系数的数量与数据点的数量呈二次增长,因此它们处理大规模数据集的能力往往受到限制。在本文中,我们提出了一个新的子空间聚类框架,称为自表达网络(Self-Expressive Network,SENet),它使用一个设计合理的神经网络来学习数据的自身表示。我们证明了我们的感知机网络不仅可以学习训练数据上具有期望性质的自表达系数,而且可以处理样本外的数据。此外,我们还证明了SENet还可以用于大规模数据集的子空间聚类。在合成数据和实际基准数据上进行的大量实验验证了该方法的有效性。特别是,SENet在MNIST、Fashion MNIST和Extended MNIST上的表现极具竞争力,在CIFAR-10上的表现堪称一流。代码可从以下网址获得:
https://github.com/zhangsz1998/Self-Expressive-Network
一、简介
随着数据采集、存储和处理技术的进步,计算机视觉中大规模数据库的可用性激增。虽然现代机器学习技术的发展,如深度学习,已经在分析大数据方面取得了巨大的成功,但是这种方法需要大量的注释数据,而这些数据的获取往往是昂贵的。从未标记的大数据中提取模式和聚类已经成为一个重要的开放性问题。我们考虑了在假设每个聚类由高维环境空间的低维子空间近似的情况下对大规模未标记数据进行聚类的问题,即子空间聚类。该问题在图像聚类、运动分割、混合系统识别、肿瘤亚型聚类、高光谱图像分割等方面有着广泛的应用。
自表达模型是最流行和最成功的子空间聚类方法之一。给定一个数据矩阵 X = [ x 1 , ⋅ ⋅ ⋅ , x N ] ∈ R D × N X=[x_1,···,x_N]∈ \mathbb{R}^{D\times N} X=[x1,⋅⋅⋅,xN]∈RD×N,其列 x i x_i xi来自 n n n个子空间的并集,自表达模型表示每个数据点 x j ∈ R D x_j∈ \mathbb{R}^D xj∈RD被用作其他数据点的线性组合,即:
x j = ∑ i ≠ j c i j x i x_j=\sum_{i\neq j}c_{ij}x_i xj=i=j∑cijxi
其中 { c i j } i ≠ j \{c_{ij}\}_{i\neq j} {cij}i=j是自表达系数(类似于attention)。自表达模型的一个值得注意的特点是,对系数最小化某些正则化函数的求解具有子空间保持性质,即非零系数 c i j c_{ij} cij只出现在位于相同子空间的 x i x_i xi和 x j x_j xj之间。因此,通过定义任意一对数据点 x i x_i xi和 x j x_j xj之间的affinity——例如 ∣ c i j ∣ + ∣ c j i ∣ |c_{ij}|+|c_{ji}| ∣cij∣+∣cji∣,可以获得正确的(即具有子空间保持性质的)聚类,并将谱聚类应用于affinity。最近的研究进一步将自表达模型的适用性扩展到数据被噪声(noise)和离群值(outlier)破坏的、在类别不均衡、或具有数据点缺失的情况下。
尽管自表达模型具有很好的经验性能和广泛的理论正确性保证,自我表达模型的局限性在于它需要求解一个大小为 N × N N\times N N×N的自表达矩阵——对于大规模数据来说这一计算量太高了。虽然基于子采样(subsampling)、矩阵素描(sketching)或学习紧凑字典(compact dictionary)的等增加子空间聚类可伸缩性的方法已经存在,但它们没有广泛的理论保证正确性,并为可伸缩性而牺牲了准确性。此外,为一组数据计算的自表达系数不能用于为先前看不见的数据生成自表达系数,这对在线环境中的学习和样本外数据提出了挑战。
在本文中,我们介绍了SENet是如何学习一个用于子空间聚类自表达模型,并且该模型可以用来处理样本外数据和大规模数据。我们的方法是基于学习这样一个函数:
f ( x i , x j ; Θ ) : R D × R D → R f(x_i,x_j;\Theta ):\mathbb{R}^D \times \mathbb{R}^D \rightarrow \mathbb{R} f(xi,xj;Θ):RD×RD→R
这可以通过带参数 Θ Θ Θ的神经网络实现, 从而满足自表达模型:
x j = ∑ i ≠ j f ( x i , x j ; Θ ) ⋅ x i x_j=\sum_{i\neq j}f(x_i,x_j;\Theta ) \cdot x_i xj=i=j∑f(xi,xj;Θ)⋅xi
*注:对比上面两个公式可以看出,该模型是同通过神经网络拟合函数 f ( x i , x j ; Θ ) f(x_i,x_j;\Theta ) f(xi,xj;Θ)并将该函数用来学习自表达模型重的affinity参数 c i j c_{ij} cij
原则上,网络参数的个数不需要随着数据集中数据的个数而变化,因此SENet可以有效地处理大规模数据。此外,在特定数据集上训练的SENet可以为来自同一数据分布的另一个数据集生成自表达系数,因此该方法可以有效地处理样本外数据。我们提出了学习 f ( x i , x j ; Θ ) f(x_i,x_j;\Theta ) f(xi,xj;Θ)的神经网络结构以及训练算法,使我们能够学习满足子空间保持性质的自表达系数。我们的实验展示了我们方法的有效性,总结如下:
- 我们证明了由训练的SENet计算得到的自表达系数与直接求解自表达系数得到的值非常接近。这使得SENet能够逼近我们想要的自表达系数。
- 我们发现在MNIST和Fashion MNIST的训练集(部分)上训练的SENet可以在测试集上产生自表达系数并获得良好的聚类性能。这说明了SENet处理样本外数据的能力。
- 我们证明,SENet可以非常有效地对包含70000多个数据点的数据集(如MNIST、Fashion MNIST和Extended MNIST)进行聚类,在MNIST、Fashion MNIST和Extended MNIST数据集上与最新技术得到的效果接近,并十分高效(训练时间极大减少);在CIFAR-10上甚至超过其它SOTA方法。
二、相关工作
深度聚类
我们的工作与许多现有的联合训练深层神经网络和学习子空间聚类的自表达系数的研究有根本性的不同。在原有的方法中,深度网络从可能不在线性子空间中的输入数据中提取使其位于线性子空间中特征,并在特征空间中应用自表达模型。相反,我们的工作假设输入数据已经存在于线性子空间中,并着重于计算自表达系数。我们的工作也与SpectralNet有相似之处,SpectralNet通过学习神经网络来优化affinty graph上的谱聚类目标以产生隐藏的embedding。但这种方法没有数据的低维建模,因此与我们的方法不同。
自表达模型
许多工作探索了子空间聚类的自表达系数的不同正则化的选择。例如,使用 ℓ 1 \mathcal \ell_1 ℓ1范数稀疏子空间聚类采用正则化方法在当子空间独立、不相交、相交甚至仿射时,最优解是子空间保持的;核范数和 ℓ 2 \mathcal \ell_2 ℓ2范数分别用于低秩和最小二乘子空间聚类,当子空间独立时,最优解是子空间保持的;将 ℓ 1 \mathcal \ell_1 ℓ1与 ℓ 2 \mathcal \ell_2 ℓ2或核范数混合的方法在提高affinity graph的连通性的同时提供了子空间保持性质的广泛理论保证。此外,还有许多关于噪声建模和自表达模型的特征学习的研究工作。
*注:在完成提交的论文时,我们注意到一份进行中的实验报告,它提出了与我们类似的想法。而该报告使用 l 2 l2 l2正则化和对自表达系数施加对称性,我们的模型采用一般的弹性网正则化,不施加对称性约束,因此具有更好的获得子空间保持性质的能力。
可伸缩子空间聚类
大规模子空间聚类由于其在实际应用中的重要性,引起了人们的广泛关注。早期的工作提出了基于子抽样的方法,对数据的随机子集进行抽样和聚类,然后对其余数据进行基于稀疏表示的分类。在这之后,有部分方法采用了两步的计算自表达系数的方法:
1)构建一个random生成的或者从数据中学习/选择的字典;
2)将每个数据点表示为字典中原子的线性组合。
特别地,受LISTA和ISTA Net等用于解决稀疏优化问题的学习优化求解器的发展推动,提出了一种联合求解自表达系数的框架,用第一步得到的字典训练神经网络逼近自表达系数,从而有效地计算出第二步中的自表达系数。原则上,这种两步方法的聚类性能随着字典的大小而增加。然而,这一问题的规模的随着字典的大小至少二次方地增加,因此使用足够大的字典可能是不可能的。
另一组方法通过将大规模优化问题分解为一系列小规模问题,从而实现高效计算,如贪婪方法、active support方法[79]或dropout策略[10]。这些方法具有广泛的正确性理论保证和优越的实证性能。然而,它们有二次方时间和内存需求,因此同样不能处理非常大规模的数据。
自注意力模型
图注意网络(graph attention networks, GAT)、Transformer、非局部神经网络(Non-local Neural Networks)中使用的自注意机制与自表达模型具有相似的思想。在这些工作中,一个数据点的(输出)特征被计算为所有数据点的(输入)特征的线性组合。与SENet相似,线性组合中的系数用神经网络计算。然而与自表达模型不同的是,这些方法利用输入特征和输出特征之间的距离来定义无监督的训练损失,而自注意方法对输出特征施加有监督的学习损失。这导致了网络体系结构设计的差异,我们将在下一章中进行解释。
三、自表达网络 SENet
3.1 模型
令 X = [ x 1 , ⋅ ⋅ ⋅ , x N ] ∈ R D × N X=[x_1,···,x_N]∈ \mathbb{R}^{D\times N} X=[x1,⋅⋅⋅,xN]∈RD×N为一组数据矩阵,它的列位于低维线性子空间 R D \mathbb{R}^{D} RD的并集。子空间聚类的自表达方法是基于对每个 j ∈ { 1 , ⋯ , N } j∈\{1,\cdots ,N\} j∈{1,⋯,N}求解一个具有以下形式的优化问题:
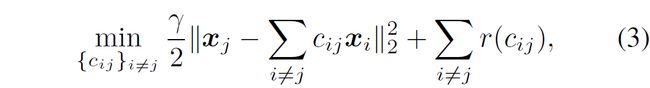
其中 r ( ⋅ ) : R ↦ R + r(\cdot):\mathbb{R}\mapsto \mathbb{R}_+ r(⋅):R↦R+是某种正则化函数而 γ > 0 \gamma >0 γ>0为平衡参数。这种思想将每个列的 x j x_j xj看做 X X X中与这些 x j ⋅ x_{j\cdot} xj⋅来自同一个子空间的其它列的线性组合,满足这种要求的线性组合就是子空间保持的,并且可以通过求解上述优化目标(3)来恢复 x j x_j xj。求解(3)得到的对每个 X X X的列的解组成了自表达系数矩阵 C ∈ R N × N C\in \mathbb R^{N\times N} C∈RN×N,矩阵的第 i i i行 j j j列的元素由 c i j c_{ij} cij得到。当矩阵 C C C是子空间保持的时候,对affinity矩阵(即 ∣ C ∣ + ∣ C T ∣ |C|+|C^T| ∣C∣+∣CT∣)进行谱聚类,能得到对数据矩阵 X X X的正确聚类结果。
*注: ↦ \mapsto ↦ = maps to
我们提出了一种基于解决以下优化问题的方法来代替优化(3):
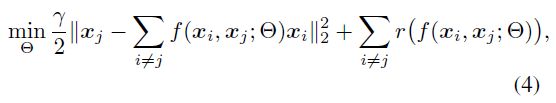
用带参数 Θ \Theta Θ的函数 f ( x i , x j ; Θ ) f(x_i,x_j;\Theta ) f(xi,xj;Θ)来代替公式(3)的模型有两个好处:
1)首先,公式(3)中的参数个数(所有 j ∈ { 1 , ⋯ , N } j∈ \{1,\cdots , N\} j∈{1,⋯,N} 的总和)与数据点数N成二次关系,这限制了它对大规模数据集的适用性,因为N×N矩阵不适合存储。相反,公式(4)中的参数数量则不需要与数据点的数量相关,可以根据内存的可用性灵活地确定。理论上,(4)中的模型可用于计算任意大小数据集的自表达系数。
2)根据(3)为特定数据集计算的自表达系数不适用于服从同一分布的另一个数据集。这意味着(3)中的模型不能用于处理样本外的数据点,对于这些样本外数据,需要从头开始计算自表达系数。相反,(4)中的自表达函数一旦在特定数据集上学习,就可以用来生成样本外数据的自表达系数。通过对函数 f ( x i , x j ; Θ ) f(x_i,x_j;\Theta ) f(xi,xj;Θ)正如我们在第3.2小节中进行的讨论,可以非常有效地对样本外数据进行计算。
正则化项的选择
众所周知,自表达模型中的稀疏正则化在最广泛的情况下迫使解具有子空间保持特性。例如,研究表明通过对系数的 ℓ 1 \ell_1 ℓ1正则化,(3)中的模型在假设子空间是充分分离的并且每个子空间中的点是均匀分布的情况下,即使子空间相交也能得到保持子空间的解。另一方面,稀疏正则化给出了具有过多假阴(false negative)的解,即当 x i x_i xi和 x j x_j xj来自同一子空间时,自表达系数 c i j c_{ij} cij却往往为零。这可能会导致affinity graph的连通性(connectivity issue)不良,进而导致过分割。因此,部分研究提倡使用弹性网正则化,这是一个加权的 ℓ 1 \ell_1 ℓ1和 ℓ 2 2 \ell_2^2 ℓ22的正则化,平衡参数 λ ∈ [ 0 , 1 ] λ ∈ [0, 1] λ∈[0,1]:
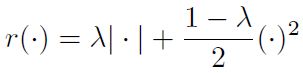
该正则化算子在与 ℓ 1 \ell_1 ℓ1正则化相似的条件下能够产生子空间保持解,同时产生更密集的系数矩阵,从而提高了聚类性能。因此我们在SENet中的正则化同样适用弹性网正则化。
3.2 网络实例化
受深度学习最新进展的启发,我们提出了自表达函数 f ( x i , x j ; Θ ) f(x_i,x_j;\Theta ) f(xi,xj;Θ)并在我们的模型中按照公式(4)训练了一个带参数 Θ Θ Θ的深度神经网络。我们把这个网络称为自表达网络(SENet)。
具体来说,我们为SENet提出以下网络公式:

其中:
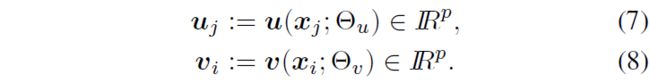
上述公式中, u ( ⋅ ; Θ u ) {u}(\cdot;\Theta_u) u(⋅;Θu)和 v ( ⋅ ; Θ v ) {v}(\cdot;\Theta_v) v(⋅;Θv)分别为query和key网络,这是两个执行 R D ↦ R p \mathbb{R}^D \mapsto \mathbb{R}^p RD↦Rp映射的多层结构(MLP),这两个网络分别具有可学习参数的 Θ u \Theta_u Θu和 Θ v \Theta_v Θv,其中p是模型参数。 τ b ( ⋅ ) \tau_b(\cdot) τb(⋅)为可学习的软阈值算子,定义为:
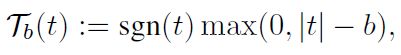
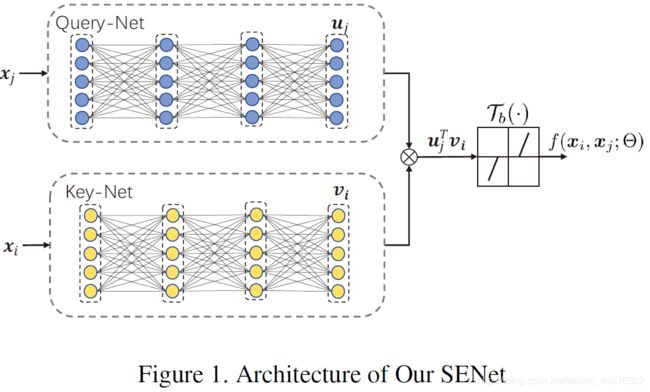
其中b是可学习的参数, α > 0 α > 0 α>0是一个固定的常数值。为了简明起见,我们定义 Θ : = { Θ u , Θ v , b } Θ:= \{Θ_u,Θ_v,b\} Θ:={Θu,Θv,b}表示SENET中所有可训练参数,并在图1中给出了该网络的结构。
通过公式(6)指导得到SENet的网络体系结构的设计,该网络通过学习一对表示 u j u_j uj和 v i v_i vi,并在应用软阈值函数之前取 u j u_j uj和 v i v_i vi的内积来计算一对数据点 ( x j , x i ) (x_j,x_i) (xj,xi)的自表达系数。我们根据经验发现(见第4.1节)这样的网络可以产生很好地逼近公式(3)解得的自表达系数,这证明了它能够获得所需的子空间保持性质和更好的连通性。
*注:对其逼近能力的分析留待以后的工作。
按照公式(6)设计的一个重要优点是:对于给定的数据矩阵 X X X,它可以非常有效地计算自表达系数矩阵。特别地,与其估计 f ( x i , x j ; Θ ) f(x_i,x_j;\Theta ) f(xi,xj;Θ)的所有 N 2 N^2 N2个数据点对 ( x j , x i ) (x_j,x_i) (xj,xi),我们其实可以并行地对数据矩阵 X X X的所有列分别地估计query和key网络,即 u ( ⋅ ; Θ u ) {u}(\cdot;\Theta_u) u(⋅;Θu)和 v ( ⋅ ; Θ v ) {v}(\cdot;\Theta_v) v(⋅;Θv)。
然后,通过计算 ( u j , v i ) (uj,vi) (uj,vi)对之间的内积得到系数矩阵,再一次地,可以对其进行并行化的高效计算。这一特性还允许我们有效地训练网络,正如我们在下一小节中所解释的那样。
与自注意力机制的比较
公式(6)的网络体系结构与Transformer、Non-Local Neural Networks和Graph attention Networks等模型中的自注意力非常相似,后者也旨在计算一组信号(例如,序列、图像、视频、图上的节点)的自表达系数。然而注意到,我们选择的体系结构与自注意模型相比有几个有利的特性。
- 自注意模型中的函数 u ( ⋅ ) u(·) u(⋅)和 v ( ⋅ ) v(·) v(⋅)是线性映射,而我们的SENet使用MLPs。该设计的目的是提高SENet的表达能力,使之具有普适逼近能力,从而使其能够很容易地逼近(3)中凸优化的最优解,并具有子空间保持性。
- 自注意模型通常采用一个归一化因子,使得每个自我表达由一个凸组合(convex combination)给出。然而,这样的要求对于我们的目的来说过于严格:对于位于其中一个子空间中样本点凸壳(convex hull)顶点上的样本点,它们不能表示为其他点的凸组合。在这种情况下,自注意模型不能产生子空间保持解。
- 我们借鉴LISTA和ISTA-net等稀疏优化网络,在SENet的输出处采用软阈值算子以增强输出的稀疏性。这是基于认为(4)中模型的解与弹性网络正则化预期是稀疏的(由于公式中的 ℓ 1 \ell_1 ℓ1范数)。
3.3 训练
我们通过解决以下的优化问题,在公式(6)中训练SENet:
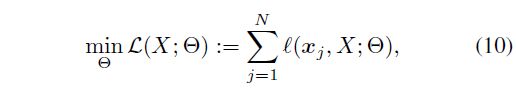
其中 ℓ ( x j , X ; Θ ) \ell(x_j,X;\Theta) ℓ(xj,X;Θ)其实就是公式(4)的优化目标函数,即:
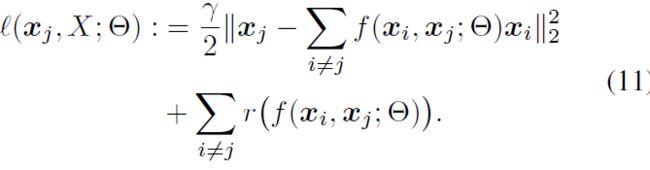
*注:这里的 i , j i,j i,j看着比较混乱,要注意 x j , j ∈ { 1 , ⋯ , N } x_j,j\in\{1,\cdots,N\} xj,j∈{1,⋯,N}是数据矩阵 X X X的每个列向量,分别被同属于数据矩阵 X X X的 x i , i ∈ { 1 , ⋯ , j − 1 , j + 1 , ⋯ , N } x_i,i\in\{1,\cdots,j-1,j+1,\cdots,N\} xi,i∈{1,⋯,j−1,j+1,⋯,N}表出,因此优化目标应当是对所有 j ∈ { 1 , ⋯ , N } j\in\{1,\cdots,N\} j∈{1,⋯,N}的 x j x_j xj列用 x i x_i xi线性组合重构的误差之和最小。
然后,网络参数 Θ Θ Θ 可以通过随机梯度下降(SGD)来学习。我们总结为算法1所示的算法(为简单起见,假设batch size 为1)。

*注:query网络先训练 x j x_j xj得到 u j u_j uj,key网络后训练 [ x 1 , ⋯ , x N ] [x_1,\cdots,x_N] [x1,⋯,xN]得到 [ v 1 , ⋯ , v N ] = V [v1,\cdots,v_N]=V [v1,⋯,vN]=V,然后计算内积,通过软阈值算子稀疏化,计算loss。
因为损失函数 ℓ ( x j , X ; Θ ) \ell(x_j,X;\Theta) ℓ(xj,X;Θ)取决于整个矩阵 X X X,算法1的内存需求随着数据点数目的增加线性扩展。这限制了算法处理大规模数据的能力。接下来,我们提出了一个与算法1等价但具有恒定内存复杂度的双道算法(算法2)。
双道算法
为了推导公式,我么首先求解梯度:
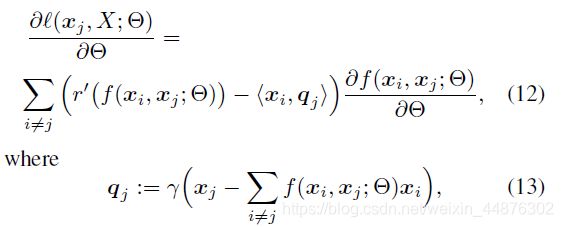

观察到,如果给出了(12)中的向量 q j q_j qj,则(12)中右手项实际是对于 i = 1 , ⋯ , N i=1,\cdots,N i=1,⋯,N的每个数据点 x i x_i xi计算得到的梯度的加权和。因此它可以被以在线的方式累加而空间需求是常数,如算法2的第14-20步所示。此外,当不知道 q j q_j qj时,它可以通过执行单独的正向传播来计算而不需要反向传播。特别地, q j q_j qj可以被通过从 x j x_j xj中减去累和 ∑ i ≠ j f ( x i , x j ; Θ ) \sum_{i\neq j}f(x_i,x_j;\Theta) ∑i=jf(xi,xj;Θ)来计算,而这个累和项同样可以在线求累和而空间需求不变,如算法2的第6-13步所示。
由于算法2的内存需求不随数据点的数量而扩展,原则上它可以处理任意大的数据集。
注: q j q_j qj本身不参与求导与反向传播,因此对于每个 x j x_j xj的 q j q_j qj都是确定的且可以在线累和的,可以先将其算出来再计算梯度。其中,如前所述地, Θ : = { Θ u , Θ v , b } Θ:= \{Θ_u,Θ_v,b\} Θ:={Θu,Θv,b},
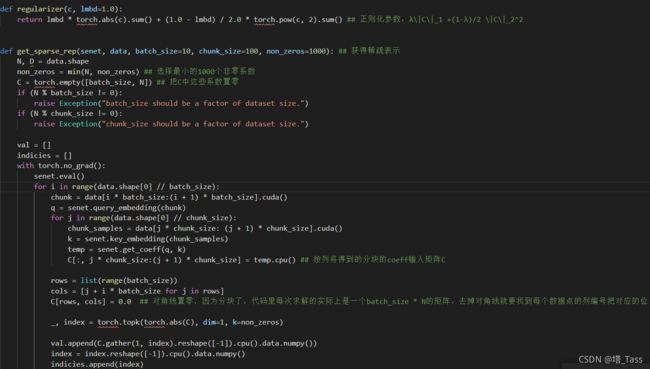
我现在并不清楚这两个网络是如何联合训练的,需要结合代码理解我现在清楚了,但是双道算法的代码并未开源,以下是算法1的解读:
四、实验
我们对综合数据和现实世界基准数据集进行了广泛的实验,以评估SENet性能。
网络架构
网络架构。对于query和key网络,我们使用了一个三层MLP,其中ReLU和tanh分别作为隐藏层和输出层的激活函数。mlp的每一层的隐单元数为 { 1024 , 1024 , 1024 } \{1024,1024,1024\} {1024,1024,1024},输出维数p为1024。通过使用tanh作为输出层激活,输出向量 u j u_j uj和 v i v_i vi的内积以p为界,即 u j T v i ∈ ( − p , p ) u_j^Tv_i∈(−p,p) ujTvi∈(−p,p)。因此,我们使用一个小的标量乘法器 α = 1 p α = \frac{1}{p} α=p1用于公式(6)以缩放传感器的输出。我们使用Adam[25]优化器,初始学习率为10−3和使用余弦退火学习率衰减与梯度剪裁(gradient clipping)。
矩阵
给定一个自表达系数矩阵 C C C,我们使用子空间恢复误差(subspace recovery error, SRE),定义为 C C C的 ℓ 1 \ell 1 ℓ1范数中来自错误子空间的比例,用来度量 C C C的子空间保持性。此外,我们使用代数连通性(algebraic connectivity, CONN),定义为在对所有ground-truth类最小化后的规范化的图拉普拉斯矩阵中第二小特征值,以度量affinity graph的连通性。如第3.1小节所述,我们希望 C C C具有低SRE和高CONN。
为了评估聚类性能,我们报告了文献中常用的聚类精度(ACC)、归一化互信息(normalized mutual information, NMI)和调整兰德系数(adjusted rand index, ARI)。
*注:RI取值范围为[0,1],值越大意味着聚类结果与真实情况越吻合——如果有了类别标签,那么聚类结果也可以像分类那样计算准确率和召回率。因为 RI 的问题在于对两个随机的划分, 其 RI 值不是一个接近于 0 的常数。Hubert和Arabie在1985年提出了调整兰德系数,假设模型的超分布为随机模型,即 X 和 Y 的划分为随机的,那么各类别和各簇的数据点数目是固定的。 A R I ∈ [ − 1 , 1 ] ARI∈[−1,1] ARI∈[−1,1]。值越大意味着聚类结果与真实情况越吻合。从广义的角度来将,ARI是衡量两个数据分布的吻合程度的。
4.1 在人工数据上的实验
自表达系数的可视化
我们证明了SENet产生自我表达系数的能力,并将其推广到合成数据上的样本外数据。为此,我们生成了一个如[81]中所述的合成数据集,其中在环境空间 R 15 \mathbb R^{15} R15(即n=5、d=6和D=15)中对5个维度为6的子空间进行单向随机采样,并在每个子空间的单位球上对200个点进行单向随机采样。随机选取500个数据点作为训练数据 X t r X_{tr} Xtr,其余500个数据点作为测试数据 X t s X_{ts} Xts。我们设定参数γ = 50.0和λ = 0.9,用算法1在最大迭代 T m a x = 500 T_{max}=500 Tmax=500的 X t r X_{tr} Xtr上训练我们的SENet,然后在第t次迭代时取训练好的SENet来计算和推断矩阵 X t r X_{tr} Xtr和 X t r X_{tr} Xtr的自表达系数 C t r ( t ) C_{tr}^{(t)} Ctr(t)和 C t s ( t ) C_{ts}^{(t)} Cts(t)。上述自表达系数的可视化如图2所示。我们观察到,经过几百次迭代后,SENet能够有效地学习近似子空间保持的自表示系数,并且训练后的SENet能够以合理的高质量推断出样本外数据的自表示系数。需要注意的是,经过300次迭代的训练,谱聚类可以得到完美的结果。
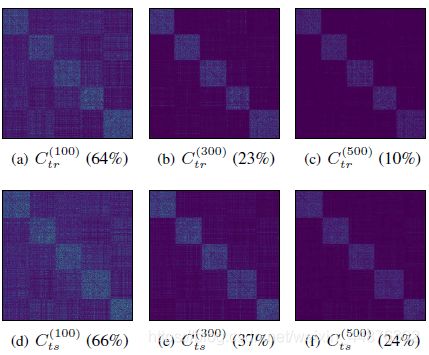
图2.用{100, 300, 500}迭代对合成数据进行训练的SENet的自表达系数的可视化,百分比指SRE。
将SENet于EnSC相比较
我们证明了SENet逼近公式(3)直接求解的能力,这是一种称为EnSC的方法[79]。为此,我们使用相同的参数γ = 50.0和λ = 0.9的SENet和EnSC模型,因此它们解决相同的优化问题。不同之处是EnSC直接优化自表达系数,而SENet优化生成系数的网络参数。
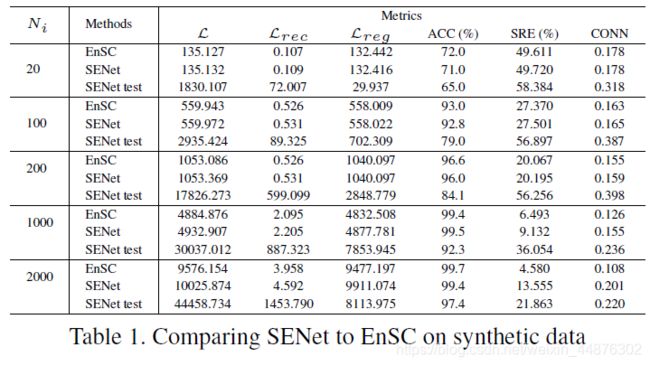
我们在环境空间 R 9 \mathbb R^{9} R9(即n=5,d=6和D=9)中抽取5个维数为6的子空间的数据点,然后从每个子空间的单位球面上抽取 N i N_i Ni个数据点 N i ∈ { 20 , 100 , 200 , 1000 , 2000 } N_i∈ \{20, 100, 200, 1000, 2000\} Ni∈{20,100,200,1000,2000}. 我们通过报告公式(10)中的总损失、重建损失和正则化损失来衡量EnSC和SENet解决方案之间的差异。
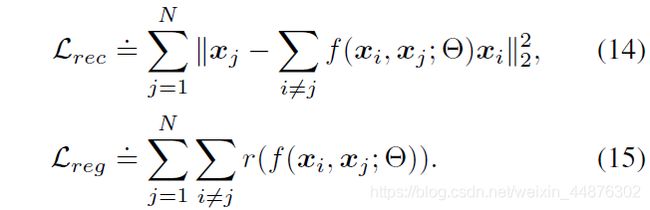
*注:重建误差的二范数平方即重建损失,对r的累和即正则化损失
我们还报告了了SRE、CONN和ACC。结果如表1所示。我们可以看到,SENet和EnSC的解之间的差异相对较小,表明SENet结构具有很强的逼近能力。另一方面,这种差异随着 N i N_i Ni的增加而增加,表明可能需要更大(例如,更深更宽)的网络。通过检查SRE和CONN的值,我们可以看到这样的差异会导致更高的子空间保持误差,但它有助于提高affinity graph的连通性。
4.2 在真实数据集上的实验
我们在四个更大的基准数据集上进一步评估了SENet的性能:MNIST、Fashion MNIST、CIFAR-10和Extended MNIST(EMNIST)。
MNIST包含70000个handrit 10位数字“0”到“9”的灰度图像,我们将其表示为MNIST full。MNIST full分为MNIST train和MNIST test,分别由60000和10000张图像组成。Fashion MNIST包含7万幅灰色不同的时尚产品图片,表示为Fashion MNIST full。MNIST相似,Fashion MNIST full分为时尚MNIST train和时尚MNIST test,分别包含60000和10000幅图像。EMNIST包含手写数字和字母的灰度图像,其中,26个小写字母的190998张图像用于26个类别的聚类问题。针对这三个MNIST数据集,利用散射卷积网络提取平移不变和变形稳定特征,然后用PCA将维数降到500个。CIFAR-10包含10个类别的60000个32x32位的彩色图像,对于CIFAR-10的图像,我们使用MCR 2 ^2 2提取特征表示,它通过自监督学习从数据中学习子空间的并集表示。所有特征向量都被 ℓ 2 \ell_2 ℓ2规范化。
*注:对于EMNIST,我们也删除了PCA后的means
为了根据自表达系数矩阵进行分割,我们通过如下方法(其中一种)计算affinity矩阵:
- 从系数矩阵 C C C的列构造3-最近邻图(对于MNIST、Fashion MNIST和EMNIST)。
- 通过 ∣ C ∣ + ∣ C T ∣ |C|+|C^T| ∣C∣+∣CT∣计算
然后对affinity矩阵进行谱聚类。
*注:对于MNIST和Fashion MNIST,我们使用对应于图拉普拉斯的15个最小特征值对应的特征向量来进行k-means。
SENet的泛化性能
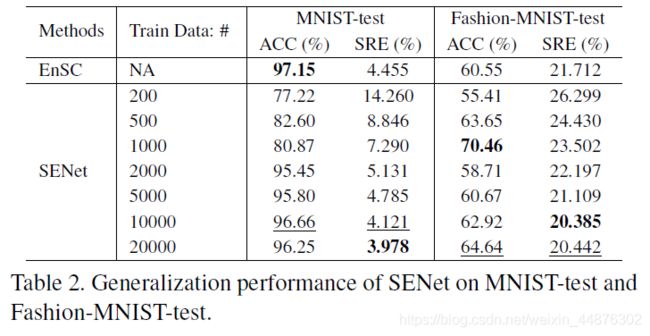
我们使用MNIST和Fashion MNIST评估了SENet对样本外数据的泛化能力。具体来说,我们从MNIST train和Fashion MNIST train随机均匀地选择 N ∈ { 200 , 500 , 1000 , 2000 , 5000 , 10000 , 20000 } N∈ \{200,500,1000,2000,5000,10000,20000\} N∈{200,500,1000,2000,5000,10000,20000}个数据点在SENet中进行100000次迭代,batch size固定为100(即每次计算batch size个Query,使用大小为N的Key作为不完备的字典去学习它的表示)。然后,我们以MNIST test和Fashion MNIST test作为测试数据,训练后的SENet用于生成自表达系数,并对诱导affinity应用谱聚类来生成分割。对于EnSC,我们直接计算了MNIST test和Fashion MNIST test的自表达系数。
实验结果如表2所示。我们可以看到,随着训练数据量的增加,SENet能够接近或超过EnSC的性能,而EnSC的性能是直接在测试数据上进行优化的。这表明训练后的SENet对实际数据集的样本外数据具有很好的泛化能力。
注:2021.11.12补足剩余实验和附录部分
SENet在大型数据集上
我们证明了SENet可以有效地处理大规模数据集MNIST-full(70000个点)、FashionMNIST-full(70000个点)、CIFAR-10(60000个点)和EMNIST(190000+的点)。对于每个数据集,我们随机选择N个点(即前面的 N ∈ { 200 , 500 , 1000 , 2000 , 5000 , 10000 , 20000 } N∈ \{200,500,1000,2000,5000,10000,20000\} N∈{200,500,1000,2000,5000,10000,20000})来训练SENet,然后应用训练后的SENet在整个数据集上生成自表达系数。最后,利用谱聚类方法进行分割。在EnSC和SENet中,我们对MNIST、时尚MNIST和CIFAR-10使用γ=200.0(正则化损失和重构损失之间的权衡参数)和λ=0.9(正则化中的 ℓ 1 \ell_1 ℓ1和 ℓ 2 \ell_2 ℓ2范数之间的权衡参数),对EMNIST使用γ=150.0和λ=1.0。
在图3中,我们报告了不同N的训练时间和聚类精度。实验在单个NVIDIA GeForce 2080Ti GPU(用于EMNIST)或1080Ti GPU(用于所有其他数据集)上进行。结果证实,我们的SENet能够在仅使用少量数据的情况下实现相当好的性能。这将大大缩短训练时间。对于EMNIST,由于EnSC需要超过24小时,我们将SENet与ESC进行比较,其中使用了300个exemplars。请注意,SENet在可接受的时间内实现了与ESC相当的性能,显示了其处理大规模数据集的潜力。
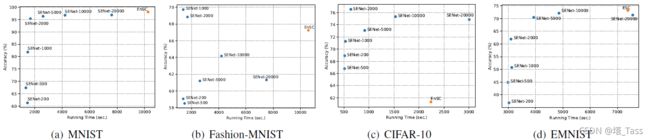
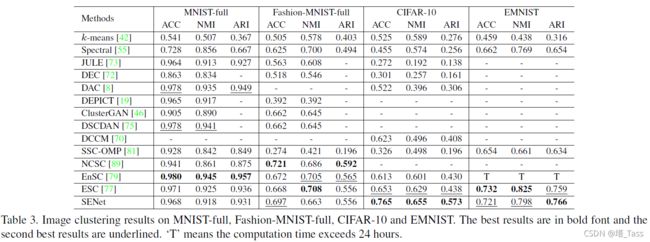
我们进一步将SENet的性能与文献中的其他方法进行了比较,实验结果如表3所示。我们可以看到,我们的SENet是四个基准中性能最好的方法之一。具体而言,SENet在CIFAR-10上的性能始终优于以前的子空间聚类方法,即在准确性方面,与EnSC相比,在CIFAR-10上的性能为+15.2%。虽然我们的SENet在小样本数据集上进行了训练,但它仍然可以在MNIST full上实现相当的性能,并且大大减少了训练时间。同时,与最先进的深度图像聚类方法相比,我们的SENet也取得了相当的性能。特别是,我们的SENet优于CIFAR-10上的所有基线方法,并在Fashion MNIST和EMNIST上实现了第二高的精确度。
附录
合成数据集上的结果
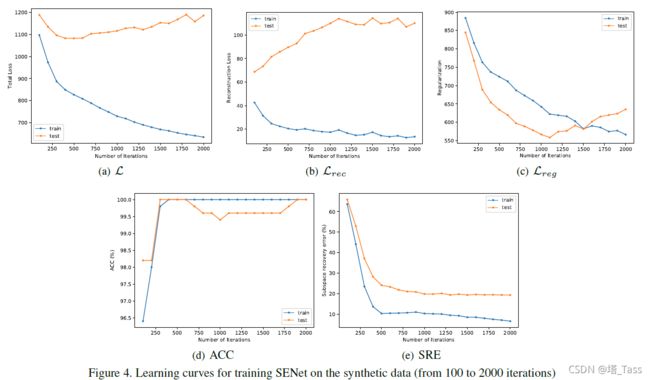
我们看到,在训练数据上,随着训练的进行,损失L及其两个分量 L r e c \mathcal L_{rec} Lrec和 L r e g \mathcal L_{reg} Lreg都单调减少。相应地,ACC单调增加,SRE单调减少。另一方面,在测试集上的 L r e c \mathcal L_{rec} Lrec单调增加,这表明SENet没有学习到测试数据的重构。尽管如此,测试数据的SRE却单调下降,表明SENet学习产生子空间保持解,从而改进了ACC。我们将关于为什么会发生这种行为的研究留给未来的工作。
SRE:子空间恢复误差,也即子空间保持误差
真实数据集上的结果(一下都以CIFAR-10为例)
Soft-Thresholding的作用
加或不加 Soft-Thresholding的性能区别非常明显:

模型设计和训练参数选择
模型深度
我们尝试{1,2,3,4}深度的Query和Key网络,同时网络宽度固定为1024。在表5中,我们报告了5次试验中ACC、NMI、ARI和SRE的平均值和标准偏差。我们可以看到,当隐藏层的数量从1增加到3时,SENet的性能会提高。但进一步增加层数无助于提高性能。请注意,即使使用单个隐藏层,SENet仍然可以很好地工作。

模型宽度
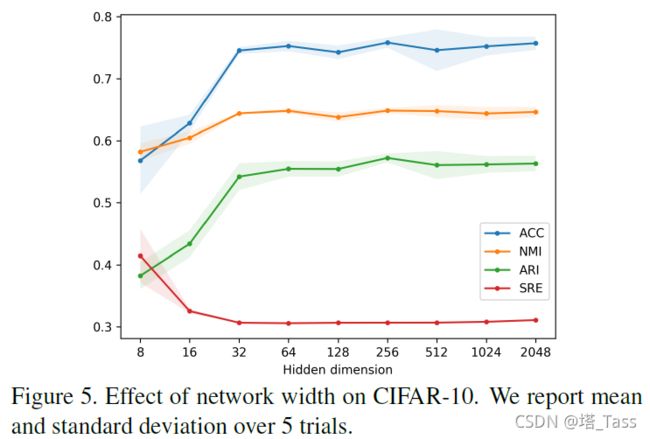
我们在8-1024范围内改变网络宽度(即每个隐藏层和输出层的神经元数量)。参数α设置为1/p。我们在图5中报告了ACC、NMI、ARI和SRE的平均值和标准偏差。我们可以看到,当网络变得更宽时,性能将继续提高。
Batch Size
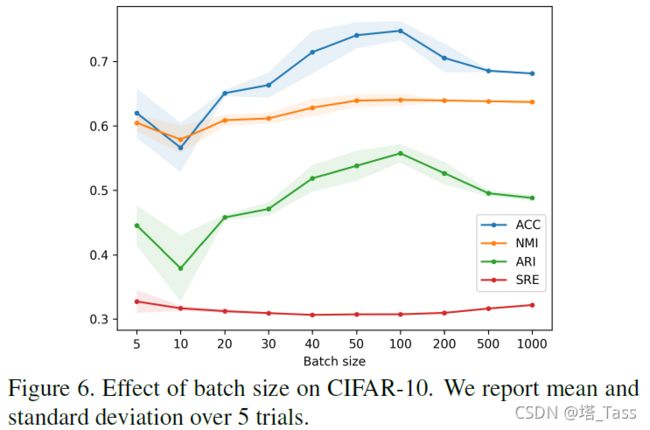
我们评估了Batch Size对训练算法的影响,并在图6中报告了ACC、NMI、ARI和SRE的平均值和标准偏差。该图显示,最佳Batch Size既不能太大也不能太小,Batch Size=100时,ACC和ARI的性能最好。
学习曲线
对于CIFAR-10,我们进一步在采样的训练数据(包含2000个数据点)以及整个CIFAR-10数据集(包含60000个数据点)上绘制ACC和SRE。5次试验计算结果的平均值和标准偏差如图7所示。我们可以看到,ACC随着迭代次数的增加而增加,而SRE先减小,然后趋于稳定。