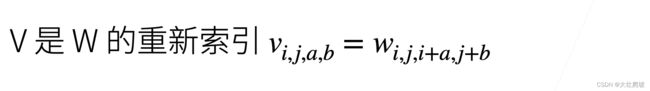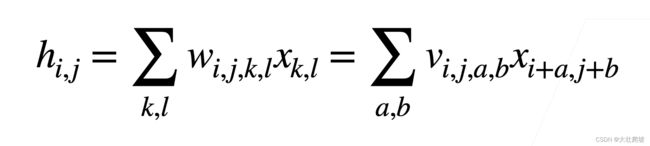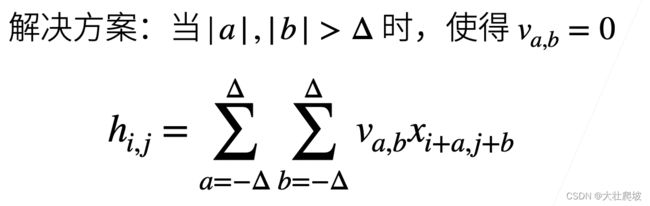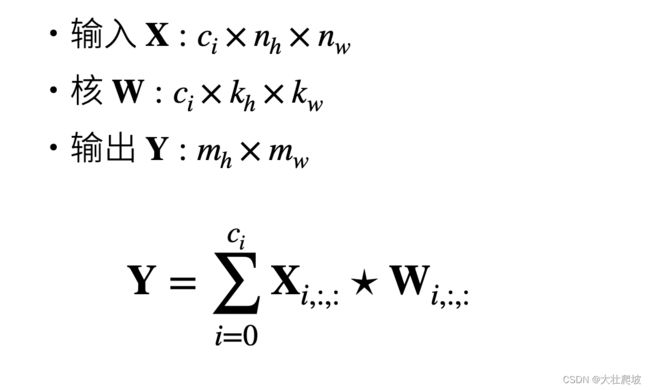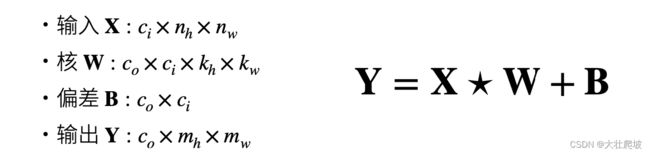笔记|李沐-动手学习机器学习|CNN基础知识(视频19-23)
李沐-动手学习机器学习|CNN基础知识
- 卷积层(视频19)
-
- 从全连接到卷积(卷积算子)
-
- 进行图像识别的两个原则
- 如何从全连接层出发,应用以上两个原则,得到卷积
- 卷积层
-
- 二维交叉相关
- 二维卷积层
- 交叉相关v.s. 卷积
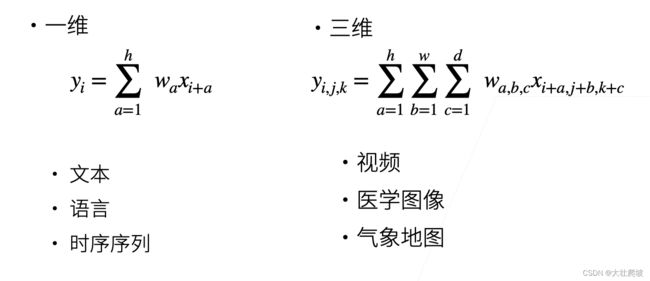
- 一维、三维交叉相关
- 卷积层里的「填充」和「步幅」(对应视频20)
-
- 填充
- 步幅
- 代码
- 卷积层里的多输入多输出通道(视频21)
-
- 多个输入通道
- 多个输出通道
- 多个输入输出通道
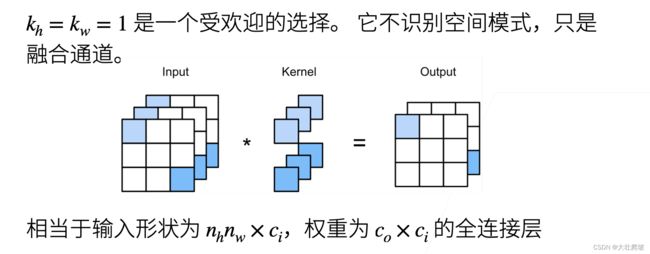
- 1*1 卷积层
- 二维卷积层
- 代码
- 池化层(视频22)
-
- 二维最大池化层
- 平均池化层
- 代码
- 经典卷积神经网络LeNet(视频23)
-
-
- LetNet实现
- 学习如何手动检查模型
-
李沐b站课程视频: 【完结】动手学深度学习 PyTorch版
卷积层(视频19)
从全连接到卷积(卷积算子)
进行图像识别的两个原则
- 平移不变性(不管目标物体在图像的哪个位置都能识别出来)
- 局部性(要识别目标物体无需遍历很广部分就能识别)
如何从全连接层出发,应用以上两个原则,得到卷积
(回顾)全连接层时,虽然图像有高、宽,但是我们会将其转变成一个1维向量。即,输入和输出均为一维向量。
(现在)将图像还原成矩阵,因为需要考虑一些空间的信息。
- 将输入输出“变形”为矩阵(高度,宽度)
- 将权重对应为4D张量((h,w)->(h‘,w’),2*2 = 4)
- 对w进行重新索引(方便后面看清实现卷积的过程)
原则 #1 平移不变性
位置变换即i,j的变化。要满足原则1,需要v的值与i,j无关,即:
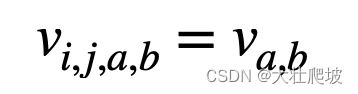
这就是「二维交叉相关」(容易错误说成“二维卷积”,但在数学上来说,这不叫卷积,而是交叉相关)
原则 #2 局部性
经过原则1,我们得到了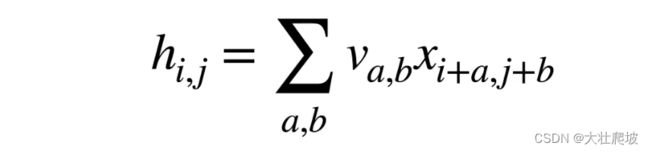
其中可以理解为以(i,j)为中心,需要遍历以外的所有a,b
但若要满足原则2,应该只需要遍历(i,j)附近的点(不应用到远离x_i,j 的参数),即:
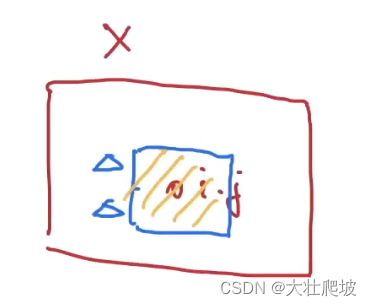
总结:对全连接层应用「平移不变性」和「不变性」得到卷积层(所以也说卷积层是一种特殊的全连接层)
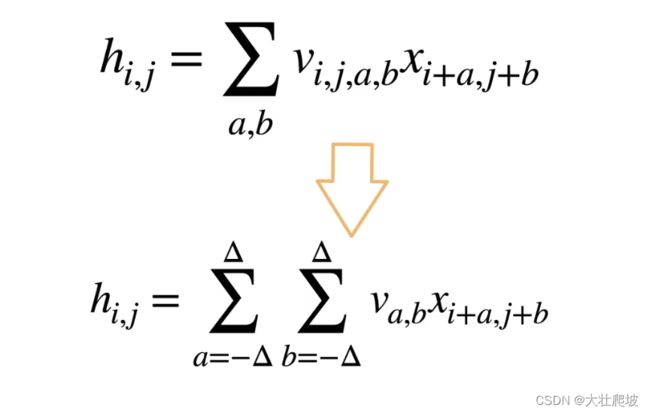
卷积层
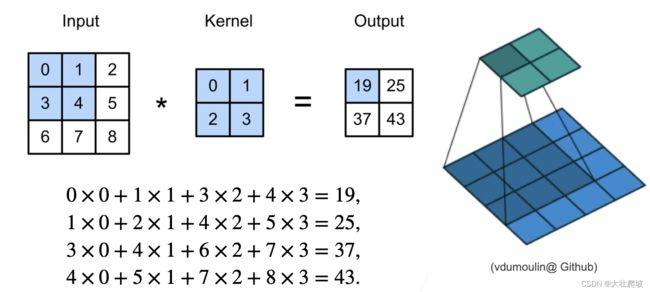
二维交叉相关
kernel就是w
二维卷积层
一个神经网络可以去学习一些不同的kernel,来得到一些不同的图像处理效果
交叉相关v.s. 卷积
唯一的区别是卷积多了个负号。但在实际应用中,由于对称性两者没有区别。而且实际常用的是交叉相关而非卷积(虽然都会叫做卷积)
一维、三维交叉相关
总结
卷积层:将核矩阵和输入进行交叉相关,再加上偏差;
可学习的参数:核矩阵、偏移
超参数:矩阵的大小
卷积层里的「填充」和「步幅」(对应视频20)
两个控制输出大小的超参数
填充
对于给定的图像,卷积核越大,输入变小地越快。
如果不希望变小地这么快,就可以用到「填充」
填充:在输入周围加入额外的行和列

这样子可以使得输入和输出的维度不变
步幅
当图片特别大,卷积核不太大,需要大量的计算才能得到较小的输出。这时就可以调整「步幅」。
步幅:是指行/列的滑动步长

总结
填充和步幅是卷积层的超参数;
填充在输入周围加入额外的行和列,控制输出形状的减少;
步幅是每次窗口核滑动的行/列步长,来成倍的减小输出形状。
代码
设定padding、stride这两个参数
在下面的例子中,我们创建一个高度和宽度为3的二维卷积层,并(在所有侧边填充1个像素)。给定高度和宽度为8的输入,则输出的高度和宽度也是8。
1)准备
import torch
from torch import nn
2)定义函数comp_conv2d
# 为了方便起见,我们定义了一个计算卷积层的函数。
# 此函数初始化卷积层权重,并对输入和输出提高和缩减相应的维数
def comp_conv2d(conv2d, X):
# 这里的(1,1)表示批量大小和通道数都是1
X = X.reshape((1, 1) + X.shape)
Y = conv2d(X)
# 省略前两个维度:批量大小和通道
return Y.reshape(Y.shape[2:])
# return Y.reshape(Y.shape)
卷积层里的多输入多输出通道(视频21)
通常要仔细设置的参数
多个输入通道
多个输出通道
多个输入输出通道
- 每个输出可以识别特定的模式
- 输入通道核 识别 并 组合输入中的模式
1*1 卷积层
二维卷积层
输出的m_h, m_w由输入以及padding、stride决定
代码
1)准备
import torch
from torch import nn
from d2l import torch as d2l
def corr2d(X, K): #@save
"""计算二维互相关运算"""
h, w = K.shape
Y = torch.zeros((X.shape[0] - h + 1, X.shape[1] - w + 1))
for i in range(Y.shape[0]):
for j in range(Y.shape[1]):
# 这里是x的局部和kernel进行「点积」,即对应位置元素相乘,而非矩阵乘法!!
Y[i, j] = (X[i:i + h, j:j + w] * K).sum()
return Y
2)多输入通道互相关运算
3)多输出通道互相关运算
池化层(视频22)
(回顾)卷积有些问题,对位置非常敏感,比如稍微的抖动可能会影响很大。
二维最大池化层
- 参数和卷积层很类似,都具有填充和步幅
- 没有可学习的参数
- 在每个输入通道应用池化层以得到相应的输出通道(没有通道融合)
- 输出通道数=输入通道数
平均池化层
总结
池化层返回窗口最大值/平均值;
主要用于缓解卷积层的位置敏感性。池化层通常接在卷积层后面;
池化层和卷积层一样,具有窗口大小、填充、步幅作为超参数。
代码
实现池化层的前向传播
import torch
from torch import nn
from d2l import torch as d2l
def pool2d(X, pool_size, mode='max'):
p_h, p_w = pool_size
Y = torch.zeros((X.shape[0] - p_h + 1, X.shape[1] - p_w + 1))
for i in range(Y.shape[0]):
for j in range(Y.shape[1]):
if mode == 'max':
Y[i, j] = X[i: i + p_h, j: j + p_w].max()
elif mode == 'avg':
Y[i, j] = X[i: i + p_h, j: j + p_w].mean()
return Y
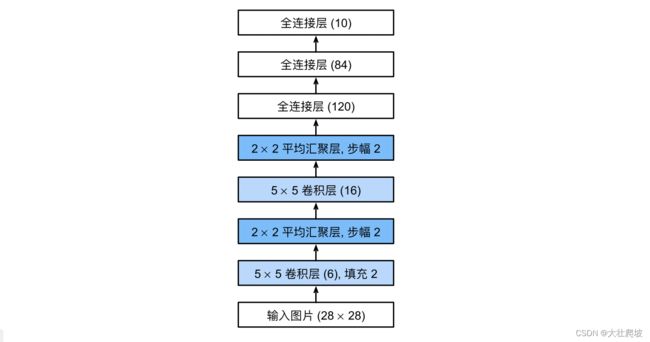
经典卷积神经网络LeNet(视频23)
背景:手写数字识别
数据集:MNIST
lenet是早期成功的神经网络
先用卷积层学习图片空间信息,然后使用全连接层转换到列别空间
当年的文章里有很多超前的内容到现在也没有实现。
LetNet实现
我们对原始模型做了一点小改动,去掉了最后一层的高斯激活。除此之外,这个网络与最初的LeNet-5一致。
import torch
from torch import nn
from d2l import torch as d2l
net = nn.Sequential(
nn.Conv2d(1, 6, kernel_size=5, padding=2), nn.Sigmoid(), # 为了得到「非线性性」,在卷积后面加一个sigmoid函数
nn.AvgPool2d(kernel_size=2, stride=2),
nn.Conv2d(6, 16, kernel_size=5), nn.Sigmoid(),
nn.AvgPool2d(kernel_size=2, stride=2),
nn.Flatten(),# 卷积层出来是个4d,要变1d输入到全连接层
nn.Linear(16 * 5 * 5, 120), nn.Sigmoid(),
nn.Linear(120, 84), nn.Sigmoid(),
nn.Linear(84, 10))
学习如何手动检查模型
可以用summerize,但是层数多网络复杂时,还是手动检查比较好
X = torch.rand(size=(1, 1, 28, 28), dtype=torch.float32)
for layer in net:
X = layer(X)
print(layer.__class__.__name__,'output shape: \t',X.shape)
核心思想:基本上可以看到卷积就是把层变小变小,通道变多变多。每个通道信息可以认为是一个pattern。不断地压缩空间信息,将能够抽出来的压缩信息放到通道里。(通道一直在增加,高宽在变小。在现在的NN里,通道可能会多到上千, 高宽最后会变成1)最后mlp就是将所有的pattern拿出来,通过一个svm模型, 训练得到最后的输出。