基于草图的图像检索-Awesome-Sketch-Based-Applications 论文笔记

Awesome-Sketch-Based-Applications 论文笔记

项目地址：https://github.com/MarkMoHR/Awesome-Sketch-Based-Applications

Sketch Based 3D Shape Retrieval

2015CVPR-Sketch-based 3D Shape Retrieval using Convolutional Neural Networks

@inproceedings{2015Sketch,
  title={Sketch-based 3D Shape Retrieval using Convolutional Neural Networks},
  author={ Wang, F.  and  Kang, L.  and  Li, Y. },
  booktitle={2015 IEEE Conference on Computer Vision and Pattern Recognition (CVPR)},
  year={2015},
}

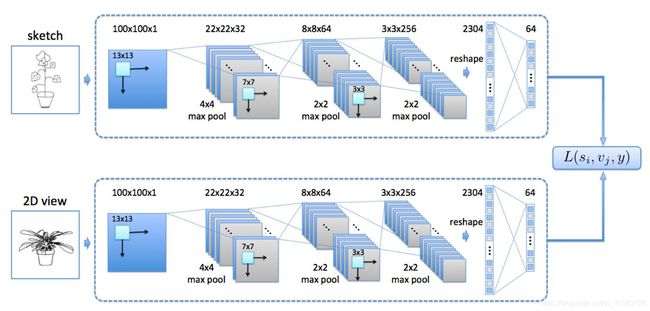
采用联合 CNN 网络进行度量学习

• 传统方法

  两阶段法：找到3D模型的最佳视角，用这些最佳视角对应的2D投影来跟手绘草图做匹配，即将由2D到3D的检索转化为由2D到2D的检索

• 本文方法

  对整个数据集使用预定义的视点，并采用两个 Siamese CNN 网络(分别用于视图和草图)进行度量学习(相似度学习，Metric Learning)

损失函数 – 度量距离函数

$$\mathcal{L}(s_1,s_2,v_1,v_2,y)=L(s_1,s_2,y)+L(v_1,v_2,y)+L(s_1,v_1,y)\text{\hspace{1em}(1)}$$

式(1)中，$L(\cdot ,\cdot ,\cdot )$ 定义为
$$L(s_1,s_2,y)=(1-y)\alpha D_w^2+y\beta e^{\gamma D_w}\text{\hspace{1em}(2)}$$
式(2)中，$y$ 代表标签；$D_w=||f(s_1;w_1)-f(s_2;w_2)$ 代表距离；设置 $\alpha =\frac{1}{C_p}$，$\beta =C_n$，$\gamma =\frac{-2.77}{C_n}$，其中$C_p=0.2$，$C_n=10$ 是常数

损失函数由三个部分组成：草图相似度(the similarity of $sketches$)、视图相似度(the similarity of views)和跨域相似度(the cross domain similarity)

2016AAAI-Learning Cross-Domain Neural Networks for Sketch-Based 3D Shape Retrieval

@inproceedings{2016Learning,
  title={Learning Cross-Domain Neural Networks for Sketch-Based 3D Shape Retrieval.},
  author={ Fan, Z.  and  Jin, X.  and F Yi},
  booktitle={Aaai},
  year={2016},
}

特定类别的神经网络 Category-Specific Neural Networks

为来自同一类的实例设置相同的目标向量，对目标层实施区分性约束

跨域神经网络设计 Cross-Domain Neural Networks

• 特征表示：2D-ScSPM，3D-LD-SIFT

• 对于草图和3D图，联合学习 CDNN 的目标函数为：
  $$\begin{array}{rl}\underset{{\mathbf{W}}_{\mathbf{s}},{\mathbf{b}}_{\mathbf{s}}}{\mathrm{argmin}}\frac{1}{P_s}& \sum _{i=1}^{P_s}{\Vert {\hat{\mathbf{x}}}_s^i-h_{{\mathbf{W}}_{\mathbf{s}},{\mathbf{b}}_{\mathbf{s}}}\left({\mathbf{x}}_{\mathbf{s}}^i\right)\Vert }_2^2+\lambda \sum _{l=1}^L{\Vert {\mathbf{W}}_{\mathbf{s}}^l\Vert }_F^2\end{array}$$

  $$\begin{gathered} \underset{{\mathbf{W}}_{\mathbf{m}},{\mathbf{b}}_m}{\mathrm{argmin}}\frac{1}{P_m}\sum _{j=1}^{P_m}{\Vert {\hat{\mathbf{x}}}_m^j-h_{{\mathbf{W}}_{\mathbf{m}},{\mathbf{b}}_{\mathbf{m}}}\left({\mathbf{x}}_{\mathbf{m}}^j\right)\Vert }_2^2+\lambda \sum _{l=1}^L{\Vert {\mathbf{W}}_{\mathbf{m}}^l\Vert }_F^2 \\ \text{ s.t. }{\hat{\mathbf{x}}}_m^i={\hat{\mathbf{x}}}_m^j={\hat{\mathbf{x}}}_s^i={\hat{\mathbf{x}}}_s^j \\ \text{ if }q\left({\mathbf{x}}_m^i\right)=q\left({\mathbf{x}}_m^j\right)=q\left({\mathbf{x}}_s^i\right)=q\left({\mathbf{x}}_s^j\right)\text{\hspace{1em}(3)} \end{gathered}$$

  可以将最优化式(3)的过程看作是分别优化2D和3D的两个网络的过程

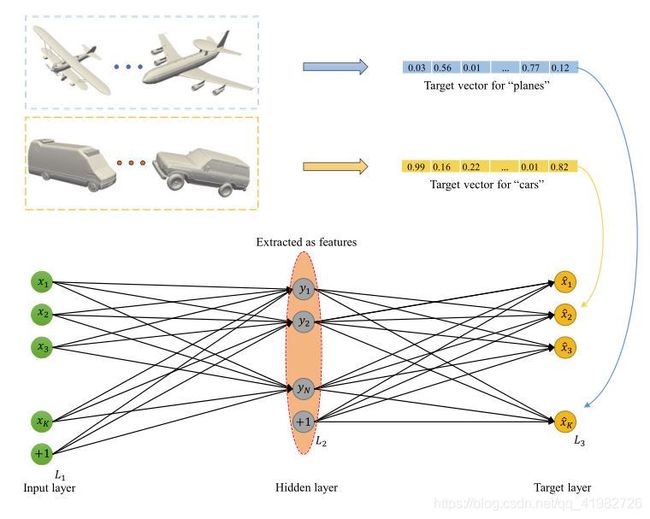
金字塔跨域神经网络设计 Pyramid Cross-Domain Neural Networks

• 目的：草图降噪，缓解草图不完整、不连续性带来的麻烦

• 遵循 ScSPM 框架来构建草图的层次表示。从草图图像的 16 × 16 的块中提取SIFT特征，并在约束投影系数稀疏性的同时投影到 1024 维的映射中。对 3 层稀疏编码使用最大池化，将草图图像分为 1 × 1、2 × 2 和 4 × 4 的 patches。替换了直接连接池化的结果与输入的全局 (1 × 1 + 2 × 2 + 4 × 4) × 1024 = 21504 维特征到神经网络中(即 CDNN 方法)，采用了提取每个金字塔层的汇总结果，并特别训练了在该层描述草图特征和3D特征之间的联系的 CDNN 模型。当草图和3D图形特征通过 PCDNN 时，提取每个金字塔网络隐含层的值，分别作为草图和3D形状的最终表示(如红色虚线矩形所示)

• 对目标函数进行了一系列优化

• 检索：定义 ${\hat{\mathbf{Y}}}_q$ 为编码查询特征，${\hat{\mathbf{Y}}}_s$ 为编码3D图形特征。为根据输入的草图查询对应的3D图形，使用式(4)计算两个特征之间的欧式距离。然后，对矩阵 $D^{’}$ 每一行进行升序排序，$D_{ij}^{{}^{\prime }}$ 的值越低，则说明对应的 ${\hat{\mathbf{Y}}}_s^j$ 和 ${\hat{\mathbf{Y}}}_q^i$ 匹配度越高
  $$D_{ij}^{\prime }\left({\hat{\mathbf{Y}}}_q,{\hat{\mathbf{Y}}}_s\right)=\sqrt{{\left({\hat{\mathbf{Y}}}_q^i-{\hat{\mathbf{Y}}}_s^j\right)}^2}\text{\hspace{1em}(4)}$$
  

2017AAAI-Deep Correlated Metric Learning for Sketch-based 3D Shape Retrieval

@article{2018Deep,
  title={Deep Correlated Holistic Metric Learning for Sketch-Based 3D Shape Retrieval},
  author={ Dai, G.  and  Jin, X.  and  Fan, Z.  and  Yi, F. },
  journal={IEEE Transactions on Image Processing A Publication of the IEEE Signal Processing Society},
  volume={27},
  number={7},
  pages={3374},
  year={2018},
}

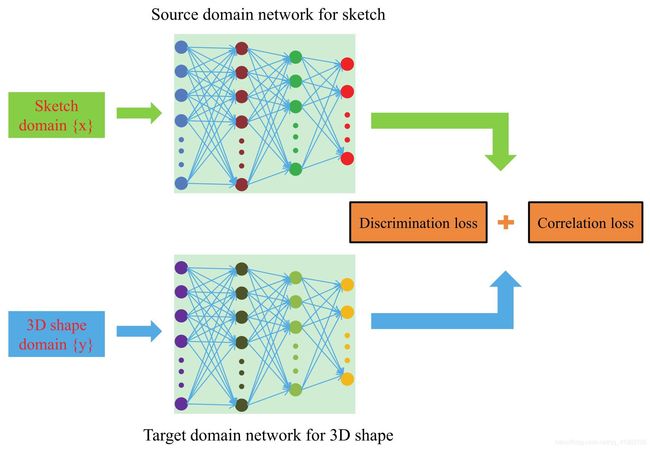
深度相关性度量学习 DCML (Deep Correlated Metric Learning)

DCML包括草图域(源域网络，SDN)和3D图形域(目标域网络，TDN)，用同相同的 loss 联合训练两个不同的深度神经网络(每个域一个)，学习两个深度非线性转换，将两个域的特征映射到一个非线性特征空间。所提出的 loss 包括对抗损失 discriminative loss 和相关性损失 correlation loss，目的是增加每个域内特征的判别性以及不同域之间的相关性。在转移空间中，对抗损失使深度转换特征的类内距离最小化，相关性损失使深度转换特征的类间距离最大化，每个域内至少有一个预定义的边缘，而相关损失则集中于使不同域之间的分布差异最小化

特征提取

• 2D草图：采用 CNN，在 Sketch 数据集上 AlexNet 微调，提取了“fc7”层的特征，维度为 4096
• 3D图形：先提取 3D-SIFT，然后用 LLC 编码，得到全局形状描述符

学习两种深度非线性变换

保证了每个领域内特征的辨别和不同领域间特征分布的一致性

1、激活函数
$$\begin{array}{l}{a}_{k+1}^{i,s}=\sigma \left(W_k^s{a}_k^{i,s}+b_k^s\right)=\sigma \left(r_{k+1}^{i,s}\right)\\ a_{k+1}^{j,t}=\sigma \left(W_k^t{a}_k^{j,t}+b_k^t\right)=\sigma \left(r_{k+1}^{j,t}\right)\end{array}\text{\hspace{1em}(5)}$$
2、非线性变换函数
$$f^s\left(x_i\right)=a_{K_s}^{i,s}{f}^t\left(y_j\right)=a_{K_t}^{j,t}\text{\hspace{1em}(6)}$$
3、损失函数
$$L=\alpha L^d+(1-\alpha )L^c+\lambda \left({\Vert W^s\Vert }_F^2+{\Vert W^t\Vert }_F^2\right)\text{\hspace{1em}(7)}$$
其中，$L^d$ 为对抗损失，在每个域内预先设定边界 $h$，使深度变化特征类内距离最小、类间距离最大；$L^c$ 是相关性损失，用于优化跨域距离，以弱化域间数据表达方式不一致的影响

损失函数的每一项都是可微的，因此 DCML 网络可以通过随机梯度下降算法的反向传播来进行优化

• 对抗损失 Discrimination term
  $$L^d=L_s^d+L_t^d\text{\hspace{1em}(8)}$$
  其中，$L_s^d$ 和 $L_t^d$ 分别代表源域和目标域的对抗损失。对抗损失由同类内正例间两两的欧式距离之和以及同类负例间两两的 hinge loss 之和组成，hinge loss 的初始间隔为 $h$

  在源域：
  $$\begin{array}{l}{L}_s^d={\sum }_{\left(x_i,x_j\right)\in P^s}{d}_{+}^s\left(x_i,x_j\right)+{\sum }_{\left(x_i,x_j\right)\in N^s}{d}_{-}^s\left(x_i,x_j\right)\\ d_{+}^s\left(x_i,x_j\right)={\Vert f^s\left(x_i\right)-f^s\left(x_j\right)\Vert }_2^2\\ d_{-}^s\left(x_i,x_j\right)=\max \left\{0,h-{\Vert f^s\left(x_i\right)-f^s\left(x_j\right)\Vert }_2^2\right\}\end{array}\text{\hspace{1em}(9)}$$
  在目标域：
  $$\begin{array}{l}{L}_t^d={\sum }_{\left(y_i,y_j\right)\in P^t}{d}_{+}^t\left(y_i,y_j\right)+{\sum }_{\left(y_i,y_j\right)\in N^t}{d}_{-}^t\left(y_i,y_j\right)\\ d_{+}^t\left(y_i,y_j\right)={\Vert f^t\left(y_i\right)-f^t\left(y_j\right)\Vert }_2^2\\ d_{-}^t\left(y_i,y_j\right)=\max \left\{0,h-{\Vert f^t\left(y_i\right)-f^t\left(y_j\right)\Vert }_2^2\right\}\end{array}\text{\hspace{1em}(10)}$$

• 相关性损失 Correlation term
  $$\begin{gathered} L^c=L_1^c+L_2^c \\ {L}_1^c=\sum _{\left(x_i,y_j\right)\in P^c}{d}_{+}^c\left(x_i,y_j\right)+\sum _{\left(x_i,y_j\right)\in N^c}{d}_{-}^c\left(x_i,y_j\right) \\ {L}_2^c=\sum _{\genfrac{}{}{0ex}{}{c^s,c^t\forall x_i,x_j\in c^s}{\forall y_i,y_j\in c^t}}R\left(x_i,x_j,y_i,y_j\right)-\sum _{c^s,d^t}^{c\ne d}\sum _{\forall x_i,x_j\in c^s}R\left(x_i,x_j,y_i,y_j\right)\text{\hspace{1em}(11)} \end{gathered}$$
  其中，$L_1^c$ 以 $h$ 为阈值，直接最小化跨域正例对的间距，同时最大化跨域负例对的间距，仅可能地使两个域的数据分布相似。$P^c$ 和 $N^c$ 分别代表跨域的正例对和负例对的集合；$d$ 的定义如下：
  $$\begin{array}{l}{d}_{+}^c\left(x_i,y_j\right)={\Vert f^s\left(x_i\right)-f^t\left(y_j\right)\Vert }_2^2\\ d_{-}^c\left(x_i,y_j\right)=\max \left\{0,h-{\Vert f^s\left(x_i\right)-f^t\left(y_j\right)\Vert }_2^2\right\}\end{array}\text{\hspace{1em}(12)}$$
  $L_2^c$ 进一步保证跨域数据的分布一致性。$c^s$ 和 $c^t$ 分别代表来自源域和目标域的分类为 $c$ 的样本集合；当两个样本来自同一个类时，$R$ 应该取最小值，否则$R$应取最大值。$R$ 的定义如下：
  $$R\left(x_i,x_j,y_i,y_j\right)=(\sqrt{{\Vert f^s\left(x_i\right)-f^s\left(x_j\right)\Vert }_2^2}-{\sqrt{{\Vert f^t\left(y_i\right)-f^t\left(y_j\right)\Vert }_2^2})}^2\text{\hspace{1em}(13)}$$

2017CVPR-Learning Barycentric Representations of 3D Shapes for Sketch-based 3D ShapeRetrieval

@inproceedings{2017Learning,
  title={Learning Barycentric Representations of 3D Shapes for Sketch-Based 3D Shape Retrieval},
  author={ Jin, X.  and  Dai, G.  and  Fan, Z.  and  Yi, F. },
  booktitle={2017 IEEE Conference on Computer Vision and Pattern Recognition (CVPR)},
  year={2017},
}

Wasserstein 距离 & Wasserstein 重心

• Wasserstein 距离

  特点：Wasserstein 距离可以描述不同概率分布之间的几何特性，不仅告诉我们两个分布之间的距离，而且能够告诉我们它们具体如何不一样，即如何从一个分布转化为另一个分布

  又称 Earth Mover’s Distance，具体定义可参考：

  【数学】Wasserstein Distance

  Wasserstein GAN and the Kantorovich-Rubinstein Duality

  Notes on Optimal Transport

• Wasserstein 重心

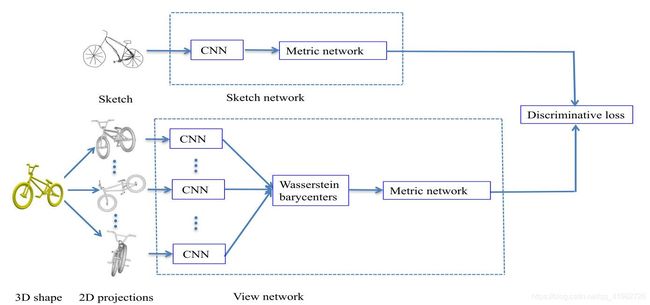
使用多视图投影的 Wasserstein 重心来描述3D图形的特征

使用 Wasserstein 重心从多个视图投影的特征空间来表征3D形状，作为一种非线性操作可以捕获结构的深层特征

均匀地缩放每个3D图形，并将形状的质心放置在球坐标系的原点。将 $V$ 个虚拟摄像机均匀地放置在3D形状周围，就可以获得 $V$ 个渲染视图。对于每个视图，将3D图形渲染为一个投影的灰度图像。一旦得到3D形状的二维投影，就可以提取二维投影的深度 CNN 特征。本文使用了 AlexNet 作为 CNN 的特征，它由五个卷积层和三个完全连接的层组成。对于每个投影，使用 ReLU 非线性激活函数后的最后一个全连通层作为深度特征，其特征大小为 4096

利用 Wasserstein 重心进行跨域匹配

提取了二维投影的深度 CNN 特征。计算深度 CNN 特征的 Wasserstein 重心来表示3D形状。利用全连通层的度量网络，设计了一个判别损失来学习草图和形状特征，用于跨域检索

损失函数：
$$\begin{gathered} \left({\hat{\mathbf{\theta }}}_1,{\hat{\mathbf{\theta }}}_2\right)={\mathrm{argmin}}_{{\mathbf{\theta }}_1,{\mathbf{\theta }}_2}\frac{1}{\sum n_j}\sum _{j=1}^{n_2}\sum _{i\in c(j)}{\Vert {\mathbf{z}}_j^2-{\mathbf{z}}_i^1\Vert }_2^2+ \\ \frac{1}{\sum m_j}\sum _{j=1}^{n_2}\sum _{i\notin c(j)}\max \left(0,\alpha -{\Vert {\mathbf{z}}_j^2-{\mathbf{z}}_i^1\Vert }_2^2\right)+{\beta }_1{L}_1+{\beta }_2{L}_2\text{\hspace{1em}(14)} \end{gathered}$$
其中，${\theta }_1=W_1,b_1$ 和 ${\theta }_2=W_2,b_2$ 是视图和草图网络的权重和偏移量，$z_i^1$ 和 $z_j^2$分别是视图网络和草图网络的输出，$n_j$ 和 $m_j$ 分别是草图的正负例样本数。$L_1$ 和 $L_2$ 是正则项，${\beta }_1$ 和 ${\beta }_2$ 是正则化参数。在式(14)中，前两项使跨域特征对之间的类内距离最小，类间距离最大。正则化项分别使3D形状特征和草图特征的类内散点最小和类间散点最大

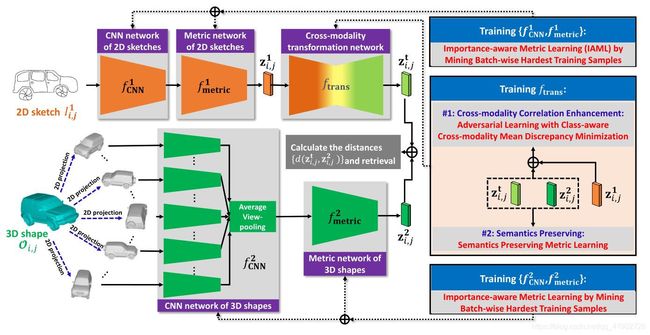
2018ECCV-Deep Cross-modality Adaptation via Semantics Preserving Adversarial Learning for Sketch-based 3D Shape Retrieval

@inproceedings{2018Deep,
  title={Deep Cross-modality Adaptation via Semantics Preserving Adversarial Learning for Sketch-based 3D Shape Retrieval},
  author={ Chen, J.  and  Fang, Y. },
  booktitle={Springer, Cham},
  year={2018},
}

基于保留语义对抗学习的深层跨模态适应模型

• 分别采用两个度量网络，在两个深度卷积神经网络(CNNs)的基础上，基于重要性感知度量学习方法学习特定模态的判别特征

• 明确引入了一种跨模态转换网络来补偿两种模态之间的差异，该网络可以将二维草图的特征转移到三维形状的特征空间

• 开发了一种基于对抗学习的方法来训练转换模型，通过同时增强两种模式数据分布之间的整体相关性，并通过最小化跨模态平均差异项来缓解局部语义差异

重要性感知特征学习 Importance-Aware Feature Learning

定义特征向量：
$${\mathbf{Z}}^m=\left\{{\mathbf{z}}_{1,1}^m,\cdots ,{\mathbf{z}}_{1,K}^m,\cdots ,{\mathbf{z}}_{C,1}^m,\cdots ,{\mathbf{z}}_{C,K}^m\right\}\text{\hspace{1em}(15)}$$
其中，$m\in \{1,2\}$，$i=1,\cdot \cdot \cdot ,C$，$j=1,\cdot \cdot \cdot ,K$，${\mathbf{z}}_{i,j}^1=f_{\text{metric }}^1\left(f_{\text{CNN }}^1\left(I_{i,j}^1\right)\right),{\mathbf{z}}_{i,j}^2=f_{\text{metric }}^2\left(f_{\text{CNN }}^2\left({\mathbf{I}}_{i,j}^2\right)\right)$

损失函数：
$$L_{IAML}^m(\left\{{\mathbf{\theta }}_{\mathbf{C}\mathbf{N}\mathbf{N}}^m,{\mathbf{\theta }}_{\mathbf{m}\mathbf{e}\mathbf{t}\mathbf{r}\mathbf{i}\mathbf{c}}^m;{\mathbf{Z}}^m\right)=\sum _i^C\sum _{j=1}^K\max \left(0,\eta -\left[{\Vert {\mathbf{z}}_{i,j}^m-{\mathbf{z}}_{i^{\ast },n^{\ast }}^m\Vert }_2-{\Vert {\mathbf{z}}_{i,j}^m-{\mathbf{z}}_{i,p^{\ast }}^m\Vert }_2\right]\right)\text{\hspace{1em}(16)}$$
其中$\eta >0$为常数，而
$$\begin{array}{r}{\mathbf{Z}}_{i^{\ast },n^{\ast }}^m={\mathrm{argmin}}_{i^{\prime }\in \{1,\cdots ,C\},y_i^{\prime }\ne y_i,n\in \{1,\cdots ,K\}}\end{array}{\Vert {\mathbf{z}}_{i,j}^m-{\mathbf{Z}}_{i^{\prime },n}^m\Vert }_2$$

$${\mathbf{z}}_{i,p^{\ast }}^m=\underset{p\in \{1,\cdots ,K\},p\ne j}{\mathrm{argmax}}{\Vert {\mathbf{z}}_{i,j}^m-{\mathbf{z}}_{i,p}^m\Vert }_2\text{\hspace{1em}(17)}$$

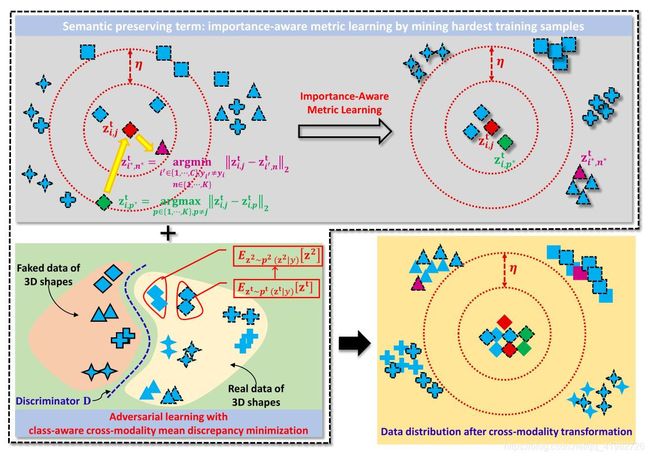
$Z_{i^{\ast },p^{\ast }}^m$ 和 $Z_{i^{\ast },n^{\ast }}^m$ 是 $z_{i,j}^m$ 的最难区分的同类样本 hardest positive samples 和最难区分的异类样本 hardest negative samples，它们在训练时都应给予较高的重要性权重，同时强制他们与语义一致，这样可以更好地学习判别特征

最小化式(16)的损失函数，等价于让最小类间间距比最大类内间距大出一个阈值 $\eta$。这样就能训练 CNN 网络和度量网络来让为每个模态生成判别特征

基于对抗学习的跨模态转换 Cross-modality Transformation based on Adversarial Learning

设$Z^t$是由$z^1$转换得来的特征，其包括以下两个要求：

• 保留语义 semantics preserving，即保持小的类内距离和大的类间距离
• 拥有关于$\{Z_{i,j}^2\}$的相关数据分布 correlated data distribution with $\{Z_{i,j}^2\}$，即拥有学习到的3D图形的特征

如图所示，模型使用了两个模块来保证上述的两个要求：

• 语义保留模块 Semantics Preserving Term

  使用式(16)和式(17)所示的损失函数来保证小的类内距离和大的类间距离

• 跨模态相关项增强模块 Cross-modality Correlation Enhancement Term

  使用GANs，训练生成器 $G$ 从噪声向量 $v$ 的数据分布 $p_x(x)$ 中采样，训练判别器 $D$ 来区分 $G$ 生成的数据和来自 $p_x(x)$ 的真实数据。
  在该模型中，GANs 的目标函数即为：
  $$\underset{f_{\text{trans }}}{\min }\underset{D}{\max }{E}_{{\mathbf{z}}^2\sim p^2\left({\mathbf{z}}^2\right)}\left[\log \left(D\left({\mathbf{z}}^2\right)\right)\right]+E_{{\mathbf{z}}^1\sim p^1\left({\mathbf{z}}^1\right)}\left[\log \left(1-D\left(f_{\text{trans }}\left({\mathbf{z}}^1\right)\right)\right)\right]\text{\hspace{1em}(18)}$$
  其中，$p^1(z^1),p^2(z^2)$ 和 $p^t(z^t)$ 分别是学习到的草图特征的分布、3D图形的特征分布和转换数据后的特征分布。当式(8)达到全局平衡时，有 $p^{\mathbf{t}}\left({\mathbf{z}}^{\mathbf{t}}\right)=p^{\mathbf{t}}\left(f_{\text{trans }}\left({\mathbf{z}}^1\right)\right)=p^2\left({\mathbf{z}}^2\right)$，即转换数据 $z^t$ 和3D图形 $z^2$ 拥有相同的数据分布。因此，将减少跨模态数据的差异

  损失函数为：
  $$L_G=E_{{\mathbf{z}}^1\sim p^1\left({\mathbf{z}}^1\right)}\left[\log \left(1-D\left({\mathbf{z}}^{\mathbf{t}}\right)\right)\right)]\text{\hspace{1em}(19)}$$

  $$L_D=-E_{{\mathbf{z}}^2\sim p^2\left({\mathbf{z}}^2\right)}\left[\log \left(D\left({\mathbf{z}}^2\right)\right)\right]-E_{{\mathbf{z}}^1\sim p^1\left({\mathbf{z}}^1\right)}\left[\log \left(1-D\left({\mathbf{z}}^{\mathbf{t}}\right)\right)\right]\text{\hspace{1em}(20)}$$

  $$L_{CMD}=\sum _y{\Vert E_{{\mathbf{z}}^{\mathbf{t}}\sim p^{\mathbf{t}}\left({\mathbf{z}}^{\mathbf{t}}\mid y\right)}\left[{\mathbf{z}}^{\mathbf{t}}\right]-E_{{\mathbf{z}}^2\sim p^2\left({\mathbf{z}}^2\mid y\right)}\left[{\mathbf{z}}^2\right]\Vert }_2\text{\hspace{1em}(21)}$$

  $L_G$ 和 $L_D$ 可以令 GANs 减少草图的变换特征和3D模型特征的分布之间的差异，$L_{CMD}$ 补充考虑了跨模态的语义结构，可以使得从草图得到的 $y$ 类平均特征向量接近于从3D形状得到的同类平均特征向量

  汇总上述所有损失函数，最终的转换模块 $f_{trans}$ 的损失函数为：
  $$L_T\left({\mathbf{\theta }}_{\text{trans }}\right)=L_{SeP}+\left(L_G+L_{CMD}\right)\text{\hspace{1em}(22)}$$

最优化方法 Optimization

• 使用 Adam 随机梯度下降法作为全程的优化器
• 使用式(16)中的 $L_{IAML}^m$ 预训练草图和3D图形的 CNN 度量网络
• 通过最小化式(19)和式(20)的 $L_T$ 和 $L_D$ 预训练跨模态转换网络
• 通过最小化 $L_{IAML}^1$、$L_{IAML}^2$、$L_T$ 和 $L_D$ 分别更新 $\{{\theta }_{CNN}^1,{\theta }_{metric}^1\}$、$\{{\theta }_{CNN}^2,{\theta }_{metric}^2\}$、${\theta }_{trans}$ 和对抗判别器 $D$

2018ACMMM-Unsupervised Learning of 3D Model Reconstruction from Hand-Drawn Sketches

@inproceedings{wang2018unsupervised,
  title={Unsupervised learning of 3d model reconstruction from hand-drawn sketches},
  author={Wang, Lingjing and Qian, Cheng and Wang, Jifei and Fang, Yi},
  booktitle={Proceedings of the 26th ACM international conference on Multimedia},
  pages={1820--1828},
  year={2018}
}

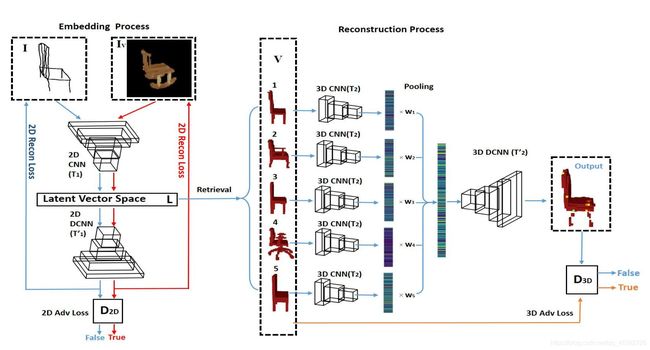
基于手绘草图三维模型重建的无监督学习 Unsupervised Learning of 3D Model Reconstruction from Hand-Drawn Sketches

• 通过带有对抗损失的自动编码器训练一个适应网络，将未配对的2D渲染图像域与手绘草图域嵌入到共享的隐藏向量空间
• 从嵌入的隐藏空间中，对于每个测试草图图像，从训练的3D数据集中检索几个(例如5个)最近的邻居，作为3D生成对抗网络的先验知识

在合成图像域内嵌入手绘草图

生成器 $G_{2D}$ 的损失函数：
$$\begin{array}{rl}{L}_{G_{2D}}\left(x,v^{\prime }\mid {\theta }_{G_{2D}}\right)& =\left(1-{\varphi }_{2D}\right)\left[L_{RE{C}_{2D}}(x)+L_{RE{C}_{2D}}\left(v^{\prime }\right)\right]+{\varphi }_{2D}{L}_{AD{V}_{2D}}\left(T_1^{\prime }{T}_1(x)\right))\end{array}$$
其中，${\varphi }_{2D}$ 是用于平衡2D重构损失和2D对抗损失的超参数，$T_1$ 和 $T_1^{\prime }$ 分别为编码器和解码器

2D重构损失为：
$$L_{RE{C}_{2D}}\left(v\mid {\theta }_{G_{2D}}\right)={\Vert T_1^{\prime }{T}_1(v)-v\Vert }_1,\forall v\in I\cup I_V\text{\hspace{1em}(23)}$$
2D对抗损失为：
$$L_{AD{V}_{2D}}\left(v\mid {\theta }_{D_{2D}}\right)={\Vert v-D_{2D}(v)\Vert }_1,\forall v\in T_1^{\prime }{T}_1(I)\cup T_1^{\prime }{T}_1\left(I_V\right)\text{\hspace{1em}(24)}$$

从共享的隐藏向量空间中检索渲染的图像

• 从训练集中的所有特征向量$z_{v_{j,k}^{\prime }}$中找到特征向量$z_{x_i}$的几个邻居，即在嵌入后从渲染的图像中找到草图图像的邻居，距离使用欧氏距离

• 检索 $K$ 个最近邻居(本文中为 5 个) $z_{v_{j,k}^{\prime }}$，分别对应在空间 $I_V$ 中的渲染图像 $v_{j,k}^{\prime }$，然后定位他们在空间 $V$ 中对应的3D对象 $v_j$

用于具有池化层的对象重建的 3D-GANS

• 生成器 $G_{3D}$

  自编码器$T_2$：拥有 200 维的瓶颈层，将 $32\times 32\times 32$ 维的3D对象编码转换为 200 维的特征向量

  池化层：生成器 $G_{3D}$ 将 $K$ 个选取的3D对象考虑为一个整体来看待，将每个对象乘以权重得到特征向量 $w={\sum }_{i=1}^K{w}_i{z}_{v_i}$(例如 $K=5$ 时，权重分别为 $0.5,0.4,0.3,0.2,0.1$，保证了最近邻可以得到更高的关注同时又不会丢失其他邻居的信息)

  解码器$T_2^{\prime }$ ：将 200 维的特征向量还原回 $32\times 32\times 32$ 维的3D对象。将池化后的特征向量 $w$ 输入解码器 $T_2^{\prime }$ 将得到重建的3D对象 $v_{OUT}$

• 判别器 $D_{3D}$

  区分3D输出对象是否跟真实的3D空间 $V$ 内的对象高度相似，若是则将其判定为"true"，否则认为其是由池化后的特征向量 $w$ 生成的，将其判定为"false"

生成器和判别器的损失函数为：
$$L_{G_{3D}}\left(v_{OUT},v\mid {\theta }_{G_{3D}}\right)=\left(1-{\varphi }_{3D}\right)\left[L_{RE{C}_{3D}}\left(v_{OUT}\right)+L_{RE{C}_{3D}}(v)\right]+{\varphi }_{3D}{L}_{AD{V}_{3D}}\left(v_{OUT}\right)\text{\hspace{1em}(25)}$$

$$L_{D_{3D}}\left(v_{OUT},v\mid {\theta }_{D_{3D}}\right)=L_{AD{V}_{3D}}(v)-k_{3D_t}{L}_{AD{V}_{3D}}\left(T_2^{\prime }{T}_2\left(v_{OUT}\right)\right)\text{\hspace{1em}(26)}$$

3D重构损失为：
$$L_{RE{C}_{3D}}\left(v\mid {\theta }_{G_{3D}}\right)={\Vert T_2^{\prime }\left(T_2(v)\right)-v\Vert }_1\text{\hspace{1em}(27)}$$
3D对抗损失为：
$$L_{AD{V}_{3D}}\left(v\mid {\theta }_{D_{3D}}\right)={\Vert v-D_{3D}(v)\Vert }_1\text{\hspace{1em}(28)}$$

2020ICME-Cross-Modal Guidance Network For Sketch-Based 3d Shape Retrieval

@inproceedings{dai2020cross,
  title={Cross-Modal Guidance Network For Sketch-Based 3d Shape Retrieval},
  author={Dai, Weidong and Liang, Shuang},
  booktitle={2020 IEEE International Conference on Multimedia and Expo (ICME)},
  pages={1--6},
  year={2020},
  organization={IEEE}
}

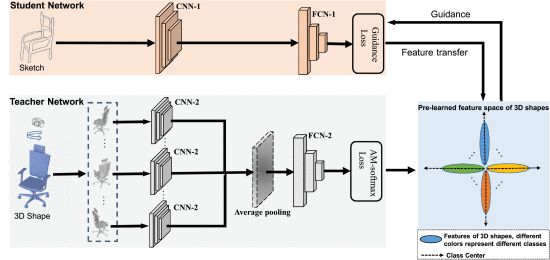
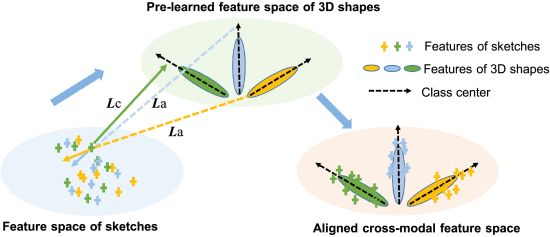
跨模态引导网络 Cross-modal Guidance Network (CGN)

• 训练教师网络学习3D图形特征，在预学习的特征空间的引导下，学生网络学习得到将草图特征转换到3D特征的映射
• 第一步：采用多视点方法提取特征，将3D图形渲染为 $V$ 视图，然后通过 CNN-2，各个CNN-2共享相同的参数，然后用平均池化融合 CNN-2 输出的特征，用 AM-softmax作为网络的损失函数。AM-softmax 可以增大类间余弦距离，减小类内余弦距离。训练完成后，3D训练数据经过 FCN-2后提取特征，得到预学习的3D形状特征空间，最后通过计算同一类特征的平均值得到类中心
• 第二步：在3D图形预学习类中心的引导下，学生网络(即转换网络)，在引导损失函数的监督下，将草图特征转换到预学习的特征空间

引导损失函数

将草图的特征转换到预学习的3D图形特征空间，同时需要确保草图特征与具有相同语义信息的类中心对齐

损失函数：
$$L_G=L_c-\lambda {\mathrm{L}}_a\text{\hspace{1em}(29)}$$

$L_c$ 是同一类中草图特征与预学习的3D图形类中心的余弦距离，即

$$L_{\mathrm{c}}=\frac{1}{M}\sum _{i=1}^M\frac{{\mathrm{f}}_i\cdot {\mathrm{c}}_{y^i}}{\Vert {\mathrm{f}}_i|{|}_2\Vert {\mathrm{c}}_{y^i}{\Vert }_2}\text{\hspace{1em}(30)}$$

$L_a$ 是草图特征与其他3D图形类中心的余弦距离之和，即

$$L_{\mathrm{a}}=\frac{1}{M}\sum _{i=1}^M\sum _{j=1,j\ne y^i}^N\frac{{\mathrm{f}}_i\cdot {\mathrm{c}}_j}{\Vert {\mathrm{f}}_i|{|}_2\Vert {\mathrm{c}}_j{\Vert }_2}\text{\hspace{1em}(31)}$$

$\lambda$ 是平衡 $L_c$ 和 $L_a$ 的超参数，$M$ 是 mini-batch 的大小，$N$ 是类别数量，$f_i$ 表示草图特征向量，$y_i$ 表示第 $i$ 个样本的标签，$\{c_1,c_2,c_N\}$ 是预学习的3D图形的类中心向量

如下图，引导损失函数旨在将草图的特征向同类3D图形的类中心聚类，同时使特征远离不同类的中心，实现了跨模态的语义对齐，减少了2D草图和3D图形之间的跨模态差异

2020CVIU-Open Cross-Domain Visual Search

@article{2020Open,
  title={Open cross-domain visual search},
  author={ Thong, W.  and  Mettes, P.  and  Snoek, Cgm },
  journal={Computer Vision and Image Understanding},
  pages={103045},
  year={2020},
}

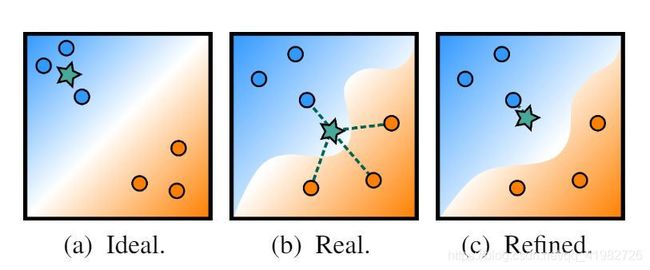
开放跨域视觉搜索 Open Cross-Domain Visual Search

可以输入任意域的数据，同时查询任意域的数据

为每个模态设计一个转换函数，将草图 sketch、自然图像 image 和3D图形的特征全部转移到一个共享的语义空间，在语义空间内执行原型学习 Prototype learning (有点像聚类)

对于一些 unseen 的类别，也可以有高于 baseline 的测试结果，即零次学习 zero-shot learning 任务也可以有不错的结果

如下图，绿色星星代表输入的查询：

• a） 理想情况下，查询的邻居仅与同一类别的实例接近

• b） 在现实中，变异性 variability 在语义空间中引起了噪声。因此，查询也可能会丢失到其他类别的样本中

• c） 通过改进查询表示来解决这种变异性：拉近查询与其最近邻的距离来修正结果

2018ECCV-Generative Domain-Migration Hashing for Sketch-to-Image Retrieval

@article{2018Generative,
  title={Generative Domain-Migration Hashing for Sketch-to-Image Retrieval},
  author={ Zhang, J.  and  Shen, F.  and  Liu, L.  and  Zhu, F.  and  Yu, M.  and  Shao, L.  and  Shen, H. T.  and  Gool, L. V. },
  journal={Springer, Cham},
  year={2018},
}

生成域迁移的哈希算法 Generative Domain-Migration Hashing

从由草图迁移过来的自然图像中生成哈希代码

• 生成器 $G_I$ 和 $G_S$ ：两个并行的生成 CNNs 网络，分别完成从草图到自然图像和从自然图像到草图的生成工作
• 判别器 $D_S$ 和 $D_I$：分别判定生成的自然图像和草图与真实样本的差异
• 哈希网络 $H$：将由判别器生成的草图和图像转换为二进制的哈希编码，并且可以基于带掩码的真实图像 $(I\odot mask)$ 和生成的图像 $G_I(S)$ 进行训练
• 损失函数：基于三元组损失

@article{2018Generative,
  title={Generative Domain-Migration Hashing for Sketch-to-Image Retrieval},
  author={ Zhang, J.  and  Shen, F.  and  Liu, L.  and  Zhu, F.  and  Yu, M.  and  Shao, L.  and  Shen, H. T.  and  Gool, L. V. },
  journal={Springer, Cham},
  year={2018},
}

生成域迁移的哈希算法 Generative Domain-Migration Hashing

从由草图迁移过来的自然图像中生成哈希代码

• 生成器 $G_I$ 和 $G_S$ ：两个并行的生成 CNNs 网络，分别完成从草图到自然图像和从自然图像到草图的生成工作
• 判别器 $D_S$ 和 $D_I$：分别判定生成的自然图像和草图与真实样本的差异
• 哈希网络 $H$：将由判别器生成的草图和图像转换为二进制的哈希编码，并且可以基于带掩码的真实图像 $(I\odot mask)$ 和生成的图像 $G_I(S)$ 进行训练
• 损失函数：基于三元组损失