bp神经网络数字识别matlab_通过深度学习神经网络，基于MNIST实现手写数字识别

通过深度学习神经网络，基于MNIST实现手写数字识别算是深度学习里的“Hello world”了，记录一下个人的实现过程。

思路

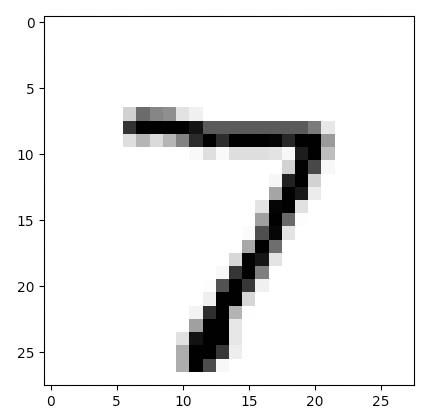
将图片格式化成28*28=784像素的灰度图片，如下图：

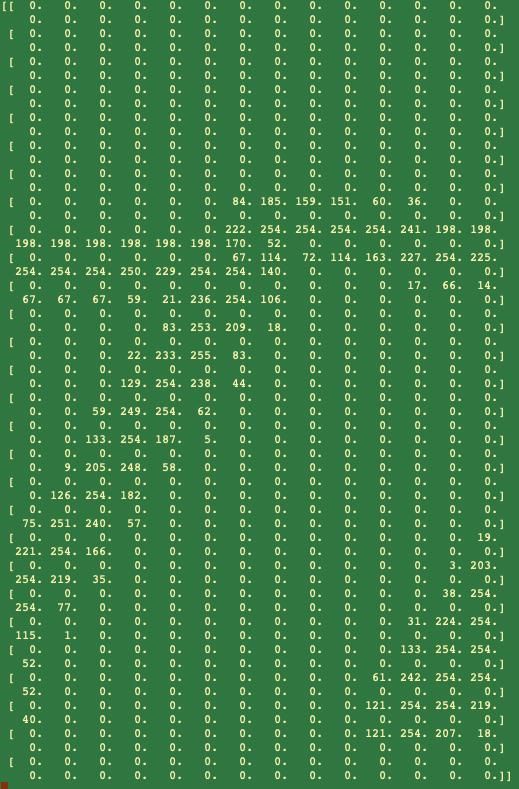
每个像素都是一个0~255的颜色值，这样我们就得到了如下数组：

此为输入层。

收集手写图片，制成标准化的图片还是很麻烦的，可以使用MNIST提供好的图片：

也可以使用已经数字化的文件：

以mnist_test_10.csv的一组数据为例，每行代表一张手写数字图片的颜色值数组，“,”分隔，第一个是手写数字的真实值。

我们将其从文件里取出来，解析并展示一下，代码：

import numpyimport matplotlib.pyplot#从文件取出数据data_file=open("mnist_test_10.csv","r")data_list=data_file.readlines()data_file.close#把数组转为图像显示，第一个数字是7allVals=data_list[0].split(",")#asfarray把数组转成浮点数组，[1:]从第2个取到最后一个元素，reshape把一维数组改成28*28的二维数组imgArr=numpy.asfarray(allVals[1:]).reshape((28,28))print(imgArr)matplotlib.pyplot.imshow(imgArr,cmap="Greys",interpolation="None")matplotlib.pyplot.show()

结果如上面的两张图。

---

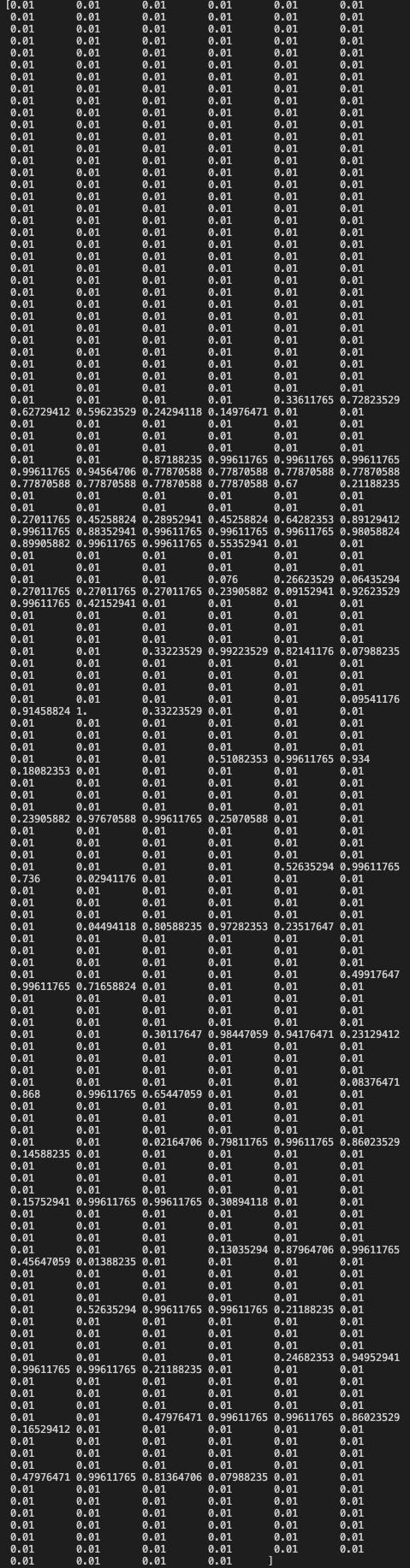
接着我们要处理一下颜色值。像素值范围是0~255，而我们接下来要使用的激活函数sigmoid的结果范围是0~1，

所以要将像素值缩小到0.01~1，不使用0作为最小值就是因为如果输入值为0，权重就失效了，0乘任何值都为0。

处理公式：像素值/255*0.99+0.01，代码如下：

newImgArr=numpy.asfarray(allVals[1:])/255.0*0.99+0.01print(newImgArr)

结果如下图：

---

最后我们要确定真实值。

输入的值，每张图有28*28=784个节点，而我们输出的时候是不需要784个节点的。

因为我们的目的是识别图片上的数字，也即这张图片是0~9的概率。

我们设一个1行10列数组，依次代表0~9。

假设有数据如下：

[0.01,0.01,0.99,0.01,0.01,0.01,0.01,0.01,0.01,0.01]

我们可以认为是数字2的概率为0.99，是其他数字的概率为0.01。

当然，也有一种可能，这个数字写的实在太难辨别了，所以会产生

[0.01,0.01,0.01,0.01,0.6,0.01,0.01,0.01,0.01,0.7]

的数据。

认为是9的概率为0.7，是4的概率0.6。

当然在实际过程中，很可能出现就是4，但结果是9的概率比较高的情况，

这不是问题，因为我们进行深度学习，求的不是精确值，而是一个概率，只要精确度逼近准确值就很好。

代码如下：

targets=numpy.zeros(10)+0.01targets[int(allVals[0])]=0.99print(targets)

整体代码

至此准备工作已经完成，开始基于前文的神经网络程序进行训练，代码如下：

# -*- coding: utf-8 -*-#!/usr/bin/python3import numpy as npimport torch as tfrom torch import nnfrom time import *class neuralNetwork:    def __init__(self,inNodes,hiddenNodes,outNodes,lr):        #输入层节点数        self.innodes=inNodes        #隐藏层节点数        self.hinodes=hiddenNodes        #输出层节点数        self.outnodes=outNodes        #学习率        self.lr=lr        #生成随机权重，一般是在正负传入链接数平方根倒数的范围内取值        np.random.seed(100)        #隐藏层1权重        self.w1=np.random.normal(0.0,pow(self.innodes,-0.5),(self.hinodes,self.innodes))        #print("权重W1")        #print(self.w1.shape)        #如果需要多个隐藏层，可在此增加        #输出层权重        self.w_final=np.random.normal(0.0,pow(self.hinodes,-0.5),(self.outnodes,self.hinodes))        #print("输出权重")        #print(self.w_final.shape)        pass    def train(self,inputs,targets):                    #计算隐藏层1结果        N1=np.dot(self.w1,inputs)        #隐藏层1激活函数        O1=t.sigmoid(t.tensor(N1)).numpy()        #print("隐藏激活层O1")        #print(O1.shape)        #print(np.transpose(O1).shape)                        #输出层结果        N_Final=np.dot(self.w_final,O1)        #输出层激活函数        O_Final=t.sigmoid(t.tensor(N_Final)).numpy()        #print("输出层O_Final")        #print(O_Final.shape)        #输出层误差矩阵        errors=targets-O_Final        #print("错误层errors")        #print(errors.shape)        #隐藏层误差矩阵w_final.T·errors        hiddenErrors=np.dot(self.w_final.T,errors)        #如果前面还多一层，则再继续转置hiddenErrors        #更新权重        #输出层权重矩阵更新公式        #w_final=w_final+Δw_final        #Δw_final=lr*[(errors*O_Final*(1-O_Final))·(O1.T)]        self.w_final += self.lr * np.dot((errors * O_Final * (1.0 - O_Final)), np.transpose(O1))        #隐藏层权重矩阵更新公式        #lr[(hiddenErrors*O1*(1-O1))·(inputs.T)]        self.w1 += self.lr * np.dot((hiddenErrors * O1 * (1.0 - O1)), np.transpose(inputs))        pass    def query(self,inputs):        N1=np.dot(self.w1,inputs)        O1=t.sigmoid(t.tensor(N1)).numpy()        N_Final=np.dot(self.w_final,O1)        O_Final=t.sigmoid(t.tensor(N_Final)).numpy()        return O_Finalbegin_time = time()#输入节点784，隐藏层节点200，输出层节点10，学习率0.1n=neuralNetwork(784,200,10,0.1)#从文件取出数据trainFile=open("mnist_train.csv","r")trains=trainFile.readlines()trainFile.closefor size in range(6):    print("第{}次训练".format(size+1))    for data in trains:        allVals=data.split(",")        inputs_list=np.asfarray(allVals[1:])/255.0*0.99+0.01        targets_list=np.zeros(10)+0.01        targets_list[int(allVals[0])]=0.99        #print("输入层")        inputs = np.array(inputs_list, ndmin=2).T        #print(inputs.shape)        #print("真实层")        targets = np.array(targets_list, ndmin=2).T        #print(targets.shape)        n.train(inputs,targets)#结果验证testFile=open("mnist_test.csv","r")tests=testFile.readlines()testFile.close#预测结果集。识别对1个数字追加1，识别错追加0，最后通过总和/长度，可以得出准确率score=[]for data in tests:    allVals=data.split(",")    realNum=int(allVals[0])    inputs_list=np.asfarray(allVals[1:])/255.0*0.99+0.01    inputs = np.array(inputs_list, ndmin=2).T    result=n.query(inputs)    outNum=np.argmax(result)    #print("真实值{}，结果值{}".format(realNum,outNum))    if(outNum==realNum):        score.append(1)    else:        score.append(0)scoreArr=np.asarray(score)print("准确率={}%".format(scoreArr.sum()/scoreArr.size*100))end_time = time()run_time = end_time-begin_timeprint ('该循环程序运行时间：',run_time)

训练和查询的代码还是深度学习神经网络监督学习笔记5-Python实现里的代码。

本文选择200个隐藏层节点，学习率0.1，使用了6W+条数据用以训练，1W+条数据用以测试，分别训练了2~7次，结果如下：

7准确率=97.26%该循环程序运行时间： 314.452527761459356准确率=97.22%该循环程序运行时间： 208.93256807327275准确率=97.18%该循环程序运行时间： 165.396576030349734准确率=96.99%该循环程序运行时间： 140.70012116532193准确率=96.86%该循环程序运行时间： 93.863017797470092准确率=96.54%该循环程序运行时间： 62.656912088394165

总结

做完之后一丝激动，一丝平静。

一个多月的辛苦，终于把深度学习的“Hello world”给做出来了。

虽然是按照教程来做的，但很多地方也加入了自己的思考和代码。

一开始学习的时候，追求的就不是依葫芦画瓢做出来，而是要认真理解其中原理、算法、工具集。

虽然这只是一个被社会淘汰的老码农在深度学习上迈出的微不足道的一步，但学习总是让人愉悦的~~

后面要增加改进的曲线图，以便直观地看到各参数对预测结果的影响，还要试着用Pytorch去实现。