概率论 ‖ Machine Learning必备知识

概率论！Machine Learning必备知识

1 什么是概率

概率亦称“或然率”，它反映随机事件出现的可能性大小，在现实生活中有着极其普遍的应用。

1.1 最简单的例子

抛硬币。

假设有一个质地均匀的硬币，也就是说这个硬币抛出后落地时正面和反面朝上的可能性是相等的。

一般我们会用符号$P$（正面）来表示硬币正面朝上的概率，其具体数值等于多次试验中正面朝上的次数除以总试验次数，即

$$P(\text{ 正面 })=\frac{\text{ 正面朝上次数 }}{\text{ 总次数 }}$$

1.2 概率论与数理统计的关系

概率论与数理统计的关系可以概括为，概率论是数理统计的理论基础，数理统计是概率论的一种应用。

例如，对于正态分布这样一种分布模型，

概率论重点研究正态分布的数学性质，如模型参数$\left(\mu ,{\sigma }^2\right)$ 对于模型稳定性的影响等；

数理统计则重点研究样本数据是否符合正态分布和参数 $\left(\mu ,{\sigma }^2\right)$ 代表的实际含义。

2 大数定律和中心极限定理

大数定律和中心极限定理可以说是概率论的核心。它们在概率论中有着无与伦比的地位。

例如，由于中心极限定理的存在，正态分布才能够从其他众多分布中脱颖而出，成为应用最为广泛的分布。实

2.1 大数定律是什么？

简单来说，大数定律告诉我们大量重复出现的随机事件中蕴含着某种必然的规律。

保持试验条件不变，多次地重复试验，随机事件出现的概率近似于它出现的频率。

例如随机抛掷硬币，在试验次数较少的情况下，硬币出现正面或反面的概率并不稳定。你抛掷10次硬币可
能出现4次正面、6次背面，也可能出现3次正面、7次背面，还可能出现8次正面、2次背面。随机事件在试验次数较少的情况下体现的就是随机性。但是随着我们增加试验次数，正面和反面出现的次数就会越来越接近，这体现出频率的稳定性。

对一般人来说，大数定律非严格的表述是这样的：$X_1,\cdots ,X_n$ 是独立同分布随机变量序列，期望为 $u$ ，且

$S_n=X_1+\cdots +X_n$ ，则 $\frac{S_n}{n}$ 收敛到 $u$。

2.2 代码直观理解大数定律

大数定律以严格的数学形式表达了随机现象的一个性质：平稳结果的稳定性或者说频率的稳定性。

下面我们用Python编写代码模拟抛硬币的过程来演示大数定律。

import random
import matplotlib.pyplot as plt


def coin_flip(min, max):  # 参数表示抛掷硬币次数大小, min代表最少抛掷次数，max 表示最多抛掷次数

    ratios = []
    x = range(min, max + 1)
    # 记录每一次抛掷的结果
    for number_Filps in x:
        numHeads = 0  # 初始化, 硬币正面朝上的计数为0
        for n in range(number_Filps):
            if random.random() < 0.5:
                numHeads += 1  # 当随机取出的数小于0.5 , 正面朝上的计数 + 1
            numTails = number_Filps - numHeads  # 用本次实验总抛掷数减去正面朝上的次数就是本次实验中反面朝上的次数
        ratios.append(numHeads / float(numTails))  # 正反面计数的比值


    plt.title("Heads / Tails Ratios")
    plt.xlabel("Numer of Flips")
    plt.ylabel("Heads / Tails")
    plt.plot(x, ratios)
    plt.hlines(1, 0, x[-1], linestyles="dashed", colors="y")
    plt.show()

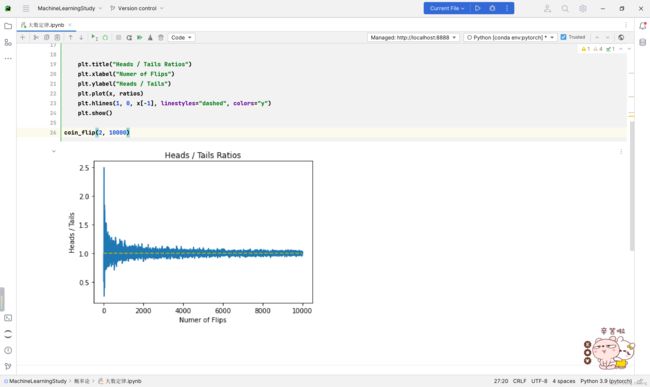
coin_flip(2, 10000)

运行结果：

可以发现，随着抛掷硬币次数的增加，硬币正反面朝上次数的比值趋近于一个稳定值1。

也就是说，大量重复试验条件下，抛掷硬币这个随机事件体现出了频率的稳定性，这其实就是大数定律想表达的内容。

2.3 中心极限定理

【1】中心极限定理是什么？

之前说的大数定律告诉我们样本均值收敛到总体均值，但是样本均值具体是如何收敛到总体均值的则没有讲明。

这就是中心极限定理要讲述的内容。中心极限定理告诉我们，当样本量足够大时，样本均值的分布围绕总体均值呈现正态分布。

【2】代码演示中心极限定理

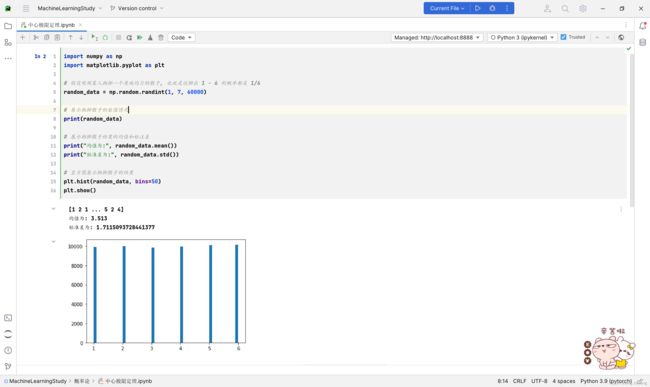
假设进行抛掷骰子试验，总共抛掷60 000次，并记录每次骰子朝上的数值。

① 总体情况

import numpy as np
import matplotlib.pyplot as plt

# 假设观测某人抛掷一个质地均匀的骰子, 也就是说掷出 1 - 6 的概率都是 1/6
random_data = np.random.randint(1, 7, 60000)

# 展示抛掷骰子的数值情况
print(random_data)

# 展示抛掷骰子结果的均值和标注差
print("均值为:", random_data.mean())
print("标准差为:", random_data.std())

# 直方图展示抛掷骰子的结果
plt.hist(random_data, bins=50)
plt.show()

运行结果

抛掷骰子结果分布比较均匀，出现次数在10 000次上下浮动。

② 单次抽样情况

我们从上述60 000次抛掷结果中，抽取100个结果作为样本来查看其均值和标准差情况。

# 从60000 次抛掷结果中, 抽取100 个结果作为样本来查看
sample_100 = []
for i in range(0, 100):
    sample_100.append(random_data[int(np.random.random() * len(random_data))])

# 展示本次从总体结果中抽取100 个结果的数值情况
print(sample_100)
# 展示本次抽取结果的均值和标准差
print("样本均值为:", np.mean(sample_100))
print("样本标准差为:", np.std(sample_100, ddof=1))

运行结果：

可以发现，单次抽样的样本均值和标准差与总体均值和标准差虽然较为接近，但是差别也明显。

③ 多次抽样情况

我们抽取50 000组、每组抽取100个结果来观察每组均值的分布情况。

print("***************** 多次抽样 ************************")
# 定义抽取 50000 组, 每组抽取100 个结果的均值和标准差列表
samples_100_mean = []
for i in range(0, 50000):
    sample = []
    for j in range(0, 100):
        sample.append(random_data[int(np.random.random() * len(random_data))])

    # 将 100 个结果的均值放入列表 samples_100_mean 中
    samples_100_mean.append(np.mean(sample))

samples_many_mean = np.mean(samples_100_mean)
print("多次抽取样本的总均值:", samples_many_mean)
plt.hist(samples_100_mean, bins=200)
plt.show()

运行结果显示，每组抽取100个结果，抽取50 000组时的总均值为3.4970636000000006，与总体均值3.4978333333333333非常接近。

将这50 000组均值通过直方图展示，可以发现这些均值形态呈现正态分布

2.4 大数定律和中心极限定理的区别

大数定律表达的核心：随着样本容量的增加，样本均值将接近总体均值。

中心极限定理表达的核心：样本独立同分布的情况下，抽样样本均值围绕总体样本均值呈现正态分布。

大数定律和中心极限定理都在描述样本的均值性质。

大数定律描述的是，随着数据量的增大，样本均值约等于总体均值。而中心极限定理描述的是，样本均值不仅接近总体均值，而且围绕总体均值呈现正态分布。大数定律揭示了大量随机变量的平均结果，但没有涉及随机变量的分布问题。而中心极限定理说明在一定条件下大量独立随机变量的平均数是以正态分布为极限的。

3 概率统计中的重要分布

3.1 正态分布

【1】正态分布是什么？

正态分布又被称为高斯分布，也称常态分布，最早由棣莫弗在求二项分布的渐近公式中得到，后来高斯在研究测量误差时从另一个角度也导出了正态分布。

正态分布的曲线形态表现为图形两头低、中间高且左右对称，因其曲线呈钟形又经常被称为钟形曲线

我们以一维数据为例，正态分布的定义：若随机变量$X$服从一个数学期望为μ、方差为${\sigma }^2$的正态分布，则可记为 $N\left(\mu ,{\sigma }^2\right)$ 。其

概率密度函数决定了正态分布的期望值μ的位置，其标准差$\sigma$决定了分布的幅度。μ = 0 ，$\sigma =1$ 的正态分布就是标准正态分布。

【2】正态分布背后的原理

其实，正态分布背后的原理就是中心极限定理。

中心极限定理说明了大量相互独立的随机变量在抽样次数足够多的时候（一般要求大于30次），每次抽取样本的均值或者和的分布情况都逼近正态分布。

中心极限定理还指出一个重要的结论：无论随机变量呈现出什么分布，只要我们抽样次数足够多，抽取样本的均值就围绕总体的均值呈现正态分布。

随着抽取组数的增多，每次抽样的均值分布越来越趋近正态分布

抽取组数 = 5

抽取组数 = 50

抽取组数 500

抽取组数 = 5000

抽取组数 = 50000

抽取组数 = 500000

中心极限定理指出大量相互独立的随机变量的均值经适当标准化后依分布收敛于正态分布，其中有3个要素：独立、随机、相加。

3.2 泊松分布

【1】泊松分布是什么？

泊松分布（Poisson分布）是一种统计学与概率学里常见到的离散概率分布，由法国数学家西梅翁·德尼·泊松在1838年发表。

公交车站根据每天客流量的变化情况来安排班次，银行根据每天的排号人数来决定开放的柜台数，书店根据图书销售情况来备货等常见的生产、生活问题都和泊松分布息息相关。

泊松分布的概率函数为 $P(X=k)=\frac{{\lambda }^k}{k!}{\mathrm{e}}^{-\lambda }$ ，$k$ = 0,1,2,3 …，

其中，参数λ指单位时间（或单位面积）内事件发生的平均概率。

泊松分布表达的含义是，单位时间里某事件发生了λ次，那么事件发生k次的概率是多少。

例如，一个公交车站有多辆不同线路的公交车，平均每10分钟就会来3辆公交车，那么10分钟内来5辆公交车的概率是多少呢？

我们根据泊松分布的公式，可以计算$P(X=k=5)=\frac{3^5}{5!}\times {\mathrm{e}}^{-3}=0.100818813445$

也就是说，这个公交车站10分钟内会有5辆公交车来的概率为10.08%。

经过研究，泊松分布适用的事件需要满足以下3个条件：

• 第一，事件是小概率事件；
• 第二，事件之间相互独立；
• 第三，事件的概率是稳定的。

一般来说，如果某事件以固定频率λ随机且独立地发生，那么该事件在单位时间内出现的次数（个数）就可以看作服从泊松分布。

【2】泊松分布的原理

要理解泊松分布的由来首先需要理解二项分布的情况，因为泊松分布是二项分布的一种极限形式，可以通过二项分布公式取极限推导出来。

抛硬币实验就是一个典型的二项分布。

假设我们抛掷n次硬币，每次抛掷后出现正面朝上的概率是$p$，那么最终出现$k$次正面朝上的概率是多少？

根据排列组合公式，n次独立事件中出现k次正面朝上的概率为 $P={\mathrm{C}}_n^k\times p^k\times (1-p{)}^{n-k}$ ，二项分布的数学期望 $\mu= np $。

那么这个二项分布和泊松分布有什么联系呢？我们还是以前面的公交车出现在站台事件为例来理解。我们将公交车到站和抛掷硬币进行类比，单位时间内公交车有两种结果：到站或者不到站。假设公交车到站是独立事件，单位时间内公交车到站的概率为p，那么公交车到站就服从二项分布。

时间内到站的公交车为k辆的概率就是 $P={\mathrm{C}}_n^k\times p^k\times (1-p{)}^{n-k}$

由于二项分布的数学期望 $\mu= np $ ，因此 有 $p=\mu /n$ 。

当 n → ∞ 时有：

$$\begin{array}{rl}P& =\underset{n\to \infty }{\lim }{C}_n^k\times p^k\times (1-p{)}^{n-k}=\underset{n\to \infty }{\lim }{C}_n^k\times {\left(\frac{\mu }{n}\right)}^k\times {\left(1-\frac{\mu }{n}\right)}^{n-k}\\ & =\underset{n\to \infty }{\lim }\frac{n(n-1)(n-2)\cdots (n-k+1)}{k!}\times {\left(\frac{\mu }{n}\right)}^k\times {\left(1-\frac{\mu }{n}\right)}^{n-k}\\ & =\underset{n\to \infty }{\lim }\frac{{\mu }^k}{k!}\times \frac{n(n-1)(n-2)\cdots (n-k+1)}{n^k}\times {\left(1-\frac{\mu }{n}\right)}^{-k}\times {\left(1-\frac{\mu }{n}\right)}^n\end{array}$$

对其中部分求极限，可以得到部分极限值如下。

$$\begin{array}{c}\underset{n\to \infty }{\lim }\frac{n(n-1)(n-2)\cdots (n-k+1)}{n^k}\times {\left(1-\frac{\mu }{n}\right)}^{-k}=1\text{ 且. }\\ \underset{n\to \infty }{\lim }{\left(1-\frac{\mu }{n}\right)}^n={\mathrm{e}}^{-\mu }\text{ 。因此, 上式可以化简为 }P=\frac{{\mu }^k}{k!}{\mathrm{e}}^{-\mu }\text{ 。这就是泊松分布的数学表达形式。 }\end{array}$$

由此可见，泊松分布可作为二项分布的极限而得到。

4 朴素贝叶斯思想

朴素贝叶斯是经典的机器学习算法，也是基于概率论的分类算法。朴素贝叶斯原理简单，容易实现，多用于文本分类问题，如垃圾邮件过滤。

朴素贝叶斯思想由“条件概率”这个概念发展而来，要理解朴素贝叶斯思想首先要理解条件概率。

4.1 理解条件概率

假设我们将一枚硬币连续抛掷3次，观察其出现正反两面的情况。

设“至少出现一次反面”为事件$A$，“3次出现相同面（同正或同反）”为事件$B$。

现在，我们已经知道了事件A发生，那么事件B发生的概率是多少呢？这里已知事件A发生而求事件B发生的概率$P(B|A)$就是条件概率。

我们以最经典的思路来分析，首先列出样本空间$S=正正正，正正反，正反正，反正正，反反正，反正反，正反反，反反反$，共计8种情况；

事件$A=正正反，正反正，反正正，反反正，反正反，正反反，反反反$， 共计7种情况

事件$B=正正正，反反反$，共计2种情况。

那么应如何定义 $P(B|A)$ 的计算公式才合理呢？

我们知道，如果没有“事件A发生”这一信息的话，那么按照古典概率的定义和计算方式，事件B发生的概率
$$P(B)=2/8=1/4$$

但是现在情况出现了变化，即我们知道了“事件A发生”这一信息了。

因此，样本空间就不再是原来的空间S而是空间$A$，即{正正反，正反正，反正正，反反正，反正反，正反反，反反反}，共计7种情况；

而事件B对应的空间则不可能出现“正正正”这种情况，事件B的空间为$P(AB)$，即{反反反}，共计1种情况。所

所以！知道了“事件A发生”这一条信息后， $P(B\mid A)=\frac{P(AB)}{P(A)}=\frac{1}{7}$

由此，我们得到条件概率计算公式 $P(B\mid A)=\frac{P(AB)}{P(A)}$

4.2 如何理解贝叶斯公式

在事件A发生的情况下，事件B发生的概率计算公式为 $P(B\mid A)=\frac{P(AB)}{P(A)}$ [①]

那么，在事件B发生的情况下，事件A发生的概率的计算公式如何呢？

不难得到 $P(A\mid B)=\frac{P(AB)}{P(B)}$ [② ]

综合 ① ② → $P(A\mid B)P(B)=P(B\mid A)P(A)$

变形就得到了贝叶斯公式 → $P(A\mid B)=\frac{P(A)P(B\mid A)}{P(B)}$ 【妙啊】

4.3 最大似然估计

拉普拉斯说“概率论只是把常识用数学公式表达出来”，实际上我们在日常生活中很多时候都在无意识地使用最大似然原理。

【1】某次考试，老师发现有两份卷子（95分和65分）忘了写名字。老师填写学生得分表时，发现平时学习成绩较好的甲同学和平时学习成绩较差的乙同学忘了写名字。那么老师怎么填写两人的成绩表呢？

我靠，确实啊

【2】我们已经知道一个袋子中有黑白两种颜色的球，总共100个，其中一种颜色的球有95个，但具体是哪种颜色并不清楚。现在随机取出一个球发现是白球。那么袋子里究竟是白球多还是黑球多呢？

我靠

对于第【1】个问题，由于甲同学平时成绩较好，因此我们猜测得分高的卷子是甲同学的；对于第【2】个问题，数量为95的某种颜色的球被我们抽中的概率更大，所以当我们抽出来的球是白球时，我们自然会认为数量为95的球是白球，也就是白球数量更多。

在上面的两个例子中，我们并没有运用什么数学公式来计算，只是凭直觉和常识。我们认为：概率最大的事件是最可能发生的，因此现实中发生的事件往往就是概率最大的那个事件。这其实就是最大似然原理的思想。

最大似然原理中的“最大似然”表示“最大概率看起来是这个样子”，所以最大似然原理的意思其实就是“最大概率看起来是这个样子，那我们认为真实情况就是这个样子”。

最大似然估计实际上就是利用最大似然原理完成一项任务：参数估计。