机器学习逐渐放弃:线性回归,逻辑回归
浑浑噩噩的混了一个月,,也不知道学了啥,就看看吴老师的视频吧。。
下面的是人家(黄老师。。)整理的作业答案吧。。写写注释,,就当作笔记了。。。
线性回归
区分一下 /* @ .dot np.mutiply:
*: 根据数据类型的不同,可能是做点乘运算,也可能做矩阵乘法运算
@: 只做矩阵乘法运算
.dot: 只做矩阵乘法运算
np.mutiply:只做点乘运算
J ( θ ) = 1 2 m ∑ i = 1 m ( h θ ( x ( i ) ) − y ( i ) ) 2 J\left( \theta \right)=\frac{1}{2m}\sum\limits_{i=1}^{m}{{{\left( {{h}_{\theta }}\left( {{x}^{(i)}} \right)-{{y}^{(i)}} \right)}^{2}}} J(θ)=2m1i=1∑m(hθ(x(i))−y(i))2
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
# 初始化数据的三个函数,,,这里只是为了省事。。还要根据实际的数据形式读取特征啊之类的。。
def get_X(df): # 读取特征
df.insert(0,'ones',1) # 插入一列 1
cols = df.shape[1]
X = df.iloc[:,0:cols-1]
return np.array(X.values) # 返回数组
def get_y(df): # 读取标签
cols = df.shape[1]
y = data.iloc[:,cols-1:cols]
return np.array(y.values) # 反正就是适应格式。。。
def normalize_feature(df): # 归一化
return df.apply(lambda column: (column - column.mean()) / column.std()))
# 计算的函数
def computercost(X, y, theta): # 代价函数
inner = np.power(((X @ theta.T) - y ),2) # X m*n theta n*1
return np.sum(inner) / (2 * len(X))
def cost2(theta,X,y): # 另一个版本
m=X.shape[0]
error = X @ theta - y
square_sum = error.T @ error
cost = square_sum / (2*m)
return cost
def gradientDescent(X, y, theta, alpha, iters): # 梯度下降
temp = np.matrix(np.zeros(theta.shape))
parameters = int(theta.ravel().shape[1])
cost = np.zeros(iters) # 每次迭代后的代价
for i in range(iters):
error = (X * theta.T) - y # X 要增加一列1.data.insert(0,'ones',1)
for j in range(parameters): # n
term = np.multiply(error, X[:,j]) # theta 1*n
temp[0,j] = theta[0,j] - ((alpha / len(X)) * np.sum(term))
theta = temp
cost[i] = computercost(X, y, theta)
return theta, cost
# 正规方程
def normalEqn(X, y):
theta = np.linalg.inv(X.T@X)@X.T@y #X.T@X等价于X.T.dot(X)
return theta
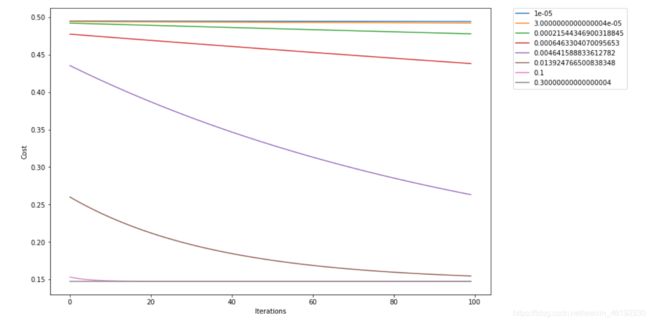
# 看看不同学习率的影响
data = pd.read_csv('ex1data1.txt',header=None,names=['Population','Profit'])
data=normalize_feature(data)
X=get_X(data)
y=get_y(data)
base = np.logspace(-1, -5, num=4) # 一堆学习率,看看不同学习率对下降的影响
candidate = np.sort(np.concatenate((base, base*3))) # 数组的拼接
print(candidate) # 大佬这么写肯定有他们的道理。。。。
>>>
[1.00000000e-05 3.00000000e-05 2.15443469e-04 6.46330407e-04
4.64158883e-03 1.39247665e-02 1.00000000e-01 3.00000000e-01]
theta = np.matrix(np.zeros(X.shape[1]))
fig, ax = plt.subplots(figsize=(12,8))
iters = 100
for i in candidate:
theta ,cost = gradientDescent(X, y, theta, i, iters)
ax.plot(np.arange(iters), cost, label=i)
ax.set_xlabel('Iterations')
ax.set_ylabel('Cost')
ax.legend(bbox_to_anchor=(1.05, 1), loc=2, borderaxespad=0.)
plt.show()
# 可以看出学习率过大,过小都是不适合的
高级版
反正目前看不懂,,就图一乐。。。。
from sklearn import linear_model
model = linear_model.LinearRegression()
model.fit(X, y)
x = np.array(X[:, 1].A1)
f = model.predict(X).flatten() # 得到的应该是拟合线上的预测值。
fig, ax = plt.subplots(figsize=(12,8))
ax.plot(x, f, 'r', label='Prediction')
ax.scatter(data.Population, data.Profit, label='Traning Data')
ax.legend(loc=2)
ax.set_xlabel('Population')
ax.set_ylabel('Profit')
ax.set_title('Predicted Profit vs. Population Size')
plt.show()
# 这个就图一乐。。。等以后在解决吧。。。
def linear_regression(X_data, y_data, alpha, epoch, optimizer=tf.train.GradientDescentOptimizer):
# placeholder for graph input
X = tf.placeholder(tf.float32, shape=X_data.shape)
y = tf.placeholder(tf.float32, shape=y_data.shape)
# construct the graph
with tf.variable_scope('linear-regression'):
W = tf.get_variable("weights",
(X_data.shape[1], 1),
initializer=tf.constant_initializer()) # n*1
y_pred = tf.matmul(X, W) # m*n @ n*1 -> m*1
loss = 1 / (2 * len(X_data)) * tf.matmul((y_pred - y), (y_pred - y), transpose_a=True) # (m*1).T @ m*1 = 1*1
opt = optimizer(learning_rate=alpha)
opt_operation = opt.minimize(loss)
# run the session
with tf.Session() as sess:
sess.run(tf.global_variables_initializer())
loss_data = []
for i in range(epoch):
_, loss_val, W_val = sess.run([opt_operation, loss, W], feed_dict={X: X_data, y: y_data})
loss_data.append(loss_val[0, 0]) # because every loss_val is 1*1 ndarray
if len(loss_data) > 1 and np.abs(loss_data[-1] - loss_data[-2]) < 10 ** -9: # early break when it's converged
# print('Converged at epoch {}'.format(i))
break
# clear the graph
tf.reset_default_graph()
return {'loss': loss_data, 'parameters': W_val} # just want to return in row vector format
逻辑回归
就是拟合出一个边界,将数据分为0,1 两类。
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
path = 'ex2data1.txt'
data = pd.read_csv(path, header=None, names=['Exam 1', 'Exam 2', 'Admitted'])
data.head()
Exam 1 Exam 2 Admitted
0 34.623660 78.024693 0
1 30.286711 43.894998 0
2 35.847409 72.902198 0
3 60.182599 86.308552 1
4 79.032736 75.344376 1
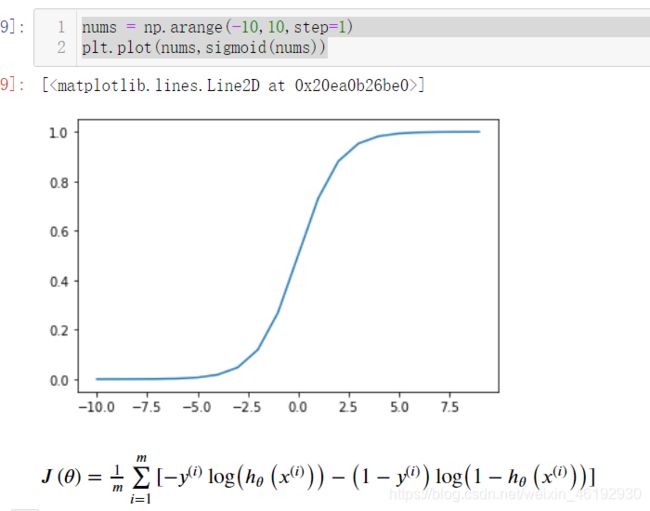
def sigmoid(z): # 就是那个Logistics函数
return 1/(1+np.exp(-z))
def cost(theta, X, y): # 代价函数
theta = np.matrix(theta)
X = np.matrix(X)
y = np.matrix(y)
first = np.multiply(-y, np.log(sigmoid(X * theta.T)))
second = np.multiply((1 - y), np.log(1 - sigmoid(X * theta.T)))
return np.sum(first - second) / (len(X))
def gradient(theta,X,y): # 梯度下降的导数部分
theta = np.matrix(theta)
X = np.matrix(X)
y = np.matrix(y)
parameters = int(theta.ravel().shape[1]) # n
grad = np.zeros(parameters)
error = sigmoid(X * theta.T) - y
for i in range(parameters):
term = np.multiply(error, X[:,i]) # X[:,0] = 1
grad[i] = np.sum(term) / len(X)
return grad
def gradient2(theta, X, y): # 这个也可以啊,更简单
return (1 / len(X)) * X.T @ (sigmoid(X @ theta.T) - y)
# y m*1 X m*n theta 1*n
def predict(theta, X): # 预测,,X 是实际数据,theta是学习出来的边界,将数据分为0,1两类
probability = sigmoid(X * theta.T)
return [1 if x >= 0.5 else 0 for x in probability] # 0.5为界线
def predict2(x, theta):
prob = sigmoid(x @ theta)
return (prob >= 0.5).astype(int) # 哇哦,这个真是厉害。。>0.5为1,小于为0
X=get_X(data)
y=get_y(data)
theta = np.matrix(np.zeros(X.shape[1]))
X.shape, theta.shape, y.shape
>>> ((100, 3), (1, 3), (100, 1))
import scipy.optimize as opt # 使用这个科学计算包进行梯度下降
result = opt.fmin_tnc(func=cost, x0=theta, fprime=gradient, args=(X, y))
result
>>> (array([-25.16131872, 0.20623159, 0.20147149]), 36, 0)
res = opt.minimize(fun=cost, x0=theta, args=(X, y), method='Newton-CG', jac=gradient)
res
>>>
fun: 0.2034977018633035
jac: array([-2.12380382e-05, -1.40885753e-03, -1.27811598e-03])
message: 'Optimization terminated successfully.' # 以一种优化,这返回的啥。。
nfev: 72
nhev: 0
nit: 28
njev: 186
status: 0
success: True
x: array([-25.16007951, 0.20622062, 0.20146256]) # 结果是一样的
from sklearn.metrics import classification_report#这个包是评价报告
def predict(x, theta):
prob = sigmoid(x @ theta)
return (prob >= 0.5).astype(int)
final_theta = res.x
y_pred = predict(X, final_theta)
print(classification_report(y, y_pred)) # 这个评价报告返回的好详细啊
>>>
precision recall f1-score support # 查准率,召回率,F1值,另一个不知道但以后会知道的
0 0.87 0.85 0.86 40
1 0.90 0.92 0.91 60
accuracy 0.89 100
macro avg 0.89 0.88 0.88 100
weighted avg 0.89 0.89 0.89 10
def accuracy(result,X,y): # 判断一下正确率
theta_min = np.matrix(result[0])
predictions = predict(theta_min, X)
correct = [1 if ((a == 1 and b == 1) or (a == 0 and b == 0)) else 0 for (a, b) in zip(predictions, y)]
# 大佬的思路就是厉害。。。
accuracy = (sum(map(int, correct)) % len(correct)) # 转换成整型在求和
print ('accuracy = {0}%'.format(accuracy))
accuracy(result,X)
>>>accuracy = 89% # 所有样本中预测正确的,应该不是查准率或召回率吧。.
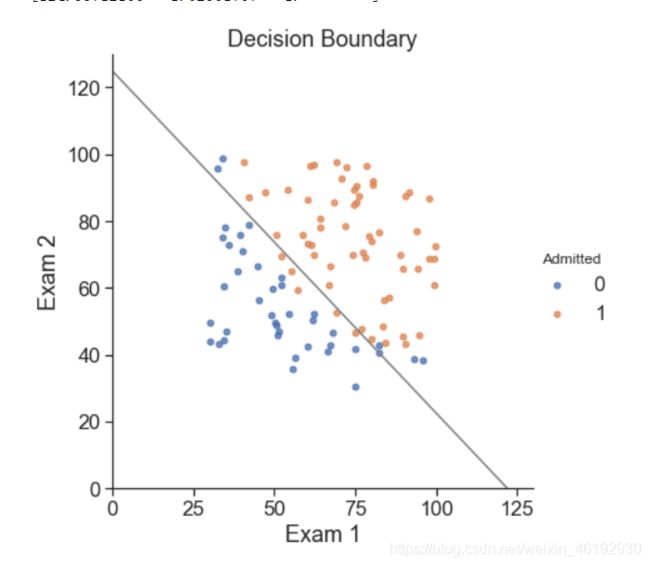
# 看一下决策边界的样子
coef = -(res.x / res.x[2]) # 构建方程,,有点迷
print(coef) # t0+ t1x1 + t2x2 = 0 -> x2 = -(t0/t2 + t1/t2 * x1)
x = np.arange(130, step=0.1)
y = coef[0] + coef[1]*x
sns.set(context="notebook", style="ticks", font_scale=1.5)
sns.lmplot('Exam 1', 'Exam 2', hue='Admitted', data=data,
size=6,
fit_reg=False,
scatter_kws={"s": 25}
)
plt.plot(x, y, 'grey')
plt.xlim(0, 130)
plt.ylim(0, 130)
plt.title('Decision Boundary')
plt.show()
正则化逻辑回归
解决过拟合的问题来着。。。
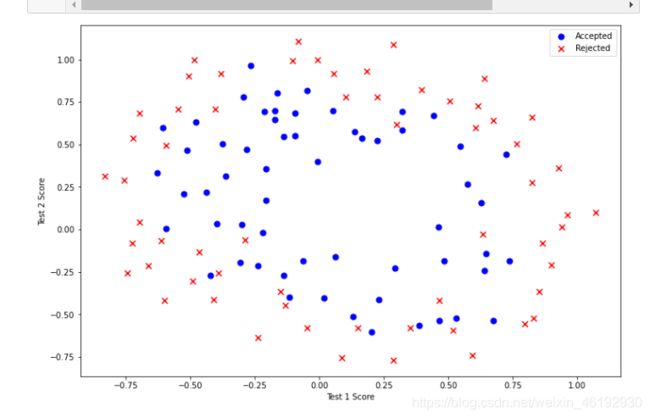
应对这种非线性的数据分类问题,构建的特征方程应该是 多项式特征。。
path = 'ex2data2.txt'
data2 = pd.read_csv(path, header=None, names=['Test 1', 'Test 2', 'Accepted'])
data2.head()
Test 1 Test 2 Accepted # 这里只有两个特征 x1, x2 再加一个 x0
0 0.051267 0.69956 1
1 -0.092742 0.68494 1 # 二维的数据应该就构建两个特征吧。。
2 -0.213710 0.69225 1
3 -0.375000 0.50219 1
4 -0.513250 0.46564 1
degree = 5
x1 = data2['Test 1']
x2 = data2['Test 2']
data2.insert(3, 'Ones', 1)
for i in range(1, degree): # 1,2,3,4
for j in range(0, i):
data2['F' + str(i) + str(j)] = np.power(x1, i-j) * np.power(x2, j) # x1**(i-j) * x2**j
# x0 x1 x1^2 x1^2*x2 x1^3 x1^3*x2 x1^3*x2^2 ............ 就类似这样的
data2.drop('Test 1', axis=1, inplace=True)
data2.drop('Test 2', axis=1, inplace=True)
data2.head()
Accepted Ones F10 F20 F21 F30 F31 F32 F40 F41 F42 F43 # 对应特征的次方
0 1 1 0.051267 0.002628 0.035864 0.000135 0.001839 0.025089 0.000007 0.000094 0.001286 0.017551
1 1 1 -0.092742 0.008601 -0.063523 -0.000798 0.005891 -0.043509 0.000074 -0.000546 0.004035 -0.029801
2 1 1 -0.213710 0.045672 -0.147941 -0.009761 0.031616 -0.102412 0.002086 -0.006757 0.021886 -0.070895
3 1 1 -0.375000 0.140625 -0.188321 -0.052734 0.070620 -0.094573 0.019775 -0.026483 0.035465 -0.047494
4 1 1 -0.513250 0.263426 -0.238990 -0.135203 0.122661 -0.111283 0.069393 -0.062956 0.057116 -0.051818
代价函数
J ( θ ) = 1 m ∑ i = 1 m [ − y ( i ) log ( h θ ( x ( i ) ) ) − ( 1 − y ( i ) ) log ( 1 − h θ ( x ( i ) ) ) ] + λ 2 m ∑ j = 1 n θ j 2 J\left( \theta \right)=\frac{1}{m}\sum\limits_{i=1}^{m}{[-{{y}^{(i)}}\log \left( {{h}_{\theta }}\left( {{x}^{(i)}} \right) \right)-\left( 1-{{y}^{(i)}} \right)\log \left( 1-{{h}_{\theta }}\left( {{x}^{(i)}} \right) \right)]}+\frac{\lambda }{2m}\sum\limits_{j=1}^{n}{\theta _{j}^{2}} J(θ)=m1i=1∑m[−y(i)log(hθ(x(i)))−(1−y(i))log(1−hθ(x(i)))]+2mλj=1∑nθj2
def costReg(theta,X,y,learningRate): # 代价函数
theta = np.matrix(theta)
y = np.matrix(y)
X = np.matrix(X) # 学习率是一种超参数,控制正则化项
first = np.multiply(-y, np.log(sigmoid(X * theta.T)))
second = np.multiply((1 - y), np.log(1 - sigmoid(X * theta.T)))
reg = (learningRate/(2*(len(X)))) * np.sum(np.power(theta[:,1:],2))
return np.sum(first - second) / len(X) + reg
def gradientReg(theta, X, y, learningRate): # 导数部分
theta = np.matrix(theta)
X = np.matrix(X)
y = np.matrix(y)
parameters = int(theta.ravel().shape[1]) # n
grad = np.zeros(parameters)
error = sigmoid(X * theta.T) - y # 一个常数
for i in range(parameters):
term = np.multiply(error, X[:,i])
if (i == 0):
grad[i] = np.sum(term) / len(X) # 对theta0 不进行正则化
else:
grad[i] = (np.sum(term) / len(X)) + ((learningRate / len(X)) * theta[:,i])
return grad # 返回数组,对应每一个theta
cols = data2.shape[1] # 还是手动构建数据的结构吧,,那啥啥函数太烦了。。
X2 = data2.iloc[:,1:cols]
y2 = data2.iloc[:,0:1]
learningRate = 1
X2 = np.array(X2.values)
y2 = np.array(y2.values)
theta2 = np.zeros(11)
X2.shape,y2.shape,theta2.shape
>>> ((118, 11), (118, 1), (11,))
result2 = opt.fmin_tnc(func=costReg, x0=theta2, fprime=gradientReg, args=(X2, y2, learningRate))
result2 # 代价函数,代价函数的导数
>>>(array([ 0.53010248, 0.29075567, -1.60725764, -0.58213819, 0.01781027,
-0.21329508, -0.40024142, -1.37144139, 0.02264304, -0.9503358 ,
0.0344085 ]),
22,
1)
accuracy(result2,X2,y2)
>>> accuracy = 78%
另一个版本,感觉更厉害些(因为看不懂),,,,
df = pd.read_csv('ex2data2.txt', names=['test1', 'test2', 'accepted'])
df.head()
test1 test2 accepted
0 0.051267 0.69956 1
1 -0.092742 0.68494 1
2 -0.213710 0.69225 1
3 -0.375000 0.50219 1
4 -0.513250 0.46564 1
def feature_mapping(x, y, power, as_ndarray=False): # 构建多项式
data = {"f{}{}".format(i - p, p): np.power(x, i - p) * np.power(y, p)
for i in np.arange(power + 1)
for p in np.arange(i + 1)
} # 虽然效果一样,但这个看着就np 。。。
if as_ndarray:
return np.pd.DataFrame(data).values # array
else:
return pd.DataFrame(data)
x1 = np.array(df.test1)
x2 = np.array(df.test2)
data = feature_mapping(x1, x2, power=6)
print(data.shape)
data.head() # 这里构建了28个多项式
f00 f10 f01 f20 f11 f02 f30 f21 f12 f03 ... f23 f14 f05 f60 f51 f42 f33 f24 f15 f06
0 1.0 0.051267 0.69956 0.002628 0.035864 0.489384 0.000135 0.001839 0.025089 0.342354 ... 0.000900 0.012278 0.167542 1.815630e-08 2.477505e-07 0.000003 0.000046 0.000629 0.008589 0.117206
1 1.0 -0.092742 0.68494 0.008601 -0.063523 0.469143 -0.000798 0.005891 -0.043509 0.321335 ... 0.002764 -0.020412 0.150752 6.362953e-07 -4.699318e-06 0.000035 -0.000256 0.001893 -0.013981 0.103256
2 1.0 -0.213710 0.69225 0.045672 -0.147941 0.479210 -0.009761 0.031616 -0.102412 0.331733 ... 0.015151 -0.049077 0.158970 9.526844e-05 -3.085938e-04 0.001000 -0.003238 0.010488 -0.033973 0.110047
3 1.0 -0.375000 0.50219 0.140625 -0.188321 0.252195 -0.052734 0.070620 -0.094573 0.126650 ... 0.017810 -0.023851 0.031940 2.780914e-03 -3.724126e-03 0.004987 -0.006679 0.008944 -0.011978 0.016040
4 1.0 -0.513250 0.46564 0.263426 -0.238990 0.216821 -0.135203 0.122661 -0.111283 0.100960 ... 0.026596 -0.024128 0.021890 1.827990e-02 -1.658422e-02 0.015046 -0.013650 0.012384 -0.011235 0.010193
5 rows × 28 columns
theta = np.zeros(data.shape[1])
print(theta.shape)
X = feature_mapping(x1, x2, power=6, as_ndarray=True) # 这里都是array 数组,,不要用矩阵啊
print(X.shape)
y=np.array(df.iloc[:,-1])
print(y.shape)
(28,)
(118, 28)
(118,)
def regularized_cost(theta, X, y, learningRate=1): # 这个大佬写的就是简洁。。。
theta_j1_to_n = theta[1:] # 不对theta0 正则化
regularized_term = (learningRate / (2 * len(X))) * np.power(theta_j1_to_n, 2).sum()
return cost(theta, X, y) + regularized_term
# 正则项前面的代价函数,在上面的逻辑回归中定义的,,就是简洁
def cost(theta, X, y):
return np.mean(-y * np.log(sigmoid(X @ theta)) - (1 - y) * np.log(1 - sigmoid(X @ theta)))
regularized_cost(theta, X, y, learningRate=1)
>>> 0.6931471805599454
def regularized_gradient(theta, X, y, l=1): # 导数部分
theta_j1_to_n = theta[1:]
regularized_theta = (l / len(X)) * theta_j1_to_n
regularized_term = np.concatenate([np.array([0]), regularized_theta])
g=gradient(theta, X, y).T
return np.array(g + regularized_term)
def gradient(theta, X, y): # 就是简洁。。。
return (1 / len(X)) * X.T @ (sigmoid(X @ theta.T) - y.T)
regularized_gradient(theta, X, y)
array([[8.47457627e-03, 1.87880932e-02, 7.77711864e-05, 5.03446395e-02,
1.15013308e-02, 3.76648474e-02, 1.83559872e-02, 7.32393391e-03,
8.19244468e-03, 2.34764889e-02, 3.93486234e-02, 2.23923907e-03,
1.28600503e-02, 3.09593720e-03, 3.93028171e-02, 1.99707467e-02,
4.32983232e-03, 3.38643902e-03, 5.83822078e-03, 4.47629067e-03,
3.10079849e-02, 3.10312442e-02, 1.09740238e-03, 6.31570797e-03,
4.08503006e-04, 7.26504316e-03, 1.37646175e-03, 3.87936363e-02]])
import scipy.optimize as opt
print('init cost = {}'.format(regularized_cost(theta, X, y)))
res = opt.minimize(fun=regularized_cost, x0=theta, args=(X, y), method='Newton-CG', jac=regularized_gradient) # 进行梯度下降
res
>>> # 这返回的啥
init cost = 0.6931471805599454
fun: 0.529002729712739
jac: array([ 7.26089191e-08, 4.22913232e-09, 8.15815876e-09, 6.15699190e-08,
7.74567232e-09, -3.09360466e-08, 2.12821347e-08, 1.22156735e-08,
1.96058084e-08, -3.19108791e-08, -4.39405717e-09, -2.76847096e-09,
-2.77934021e-08, 1.23592858e-08, -7.14474161e-08, 8.98276579e-09,
1.45962365e-08, -1.00120216e-08, -7.32796823e-09, 1.43317535e-08,
-4.38679455e-08, -4.85023121e-09, -3.40732357e-10, -1.11668147e-08,
-5.01047274e-09, -1.44326742e-08, 8.78794915e-09, -5.71951122e-08])
message: 'Optimization terminated successfully.'
nfev: 7
nhev: 0
nit: 6
njev: 57
status: 0
success: True
x: array([ 1.27273909, 0.62527214, 1.18108783, -2.01995993, -0.91742426,
-1.43166279, 0.12400726, -0.36553444, -0.35723901, -0.17513021,
-1.45815774, -0.05098947, -0.61555653, -0.27470644, -1.19281683,
-0.24218793, -0.20600565, -0.04473137, -0.27778488, -0.2953778 ,
-0.45635711, -1.04320321, 0.02777158, -0.29243198, 0.01556636,
-0.32738013, -0.14388704, -0.92465213]) # 这应该就是最优化的theta了。。
def predict(x, theta):
prob = sigmoid(x @ theta)
return (prob >= 0.5).astype(int)
from sklearn.metrics import classification_report#这个包是评价报告
final_theta = res.x
y_pred = predict(X, final_theta)
print(classification_report(y, y_pred))
>>>
precision recall f1-score support # 好长啊。。。。
0 0.90 0.75 0.82 60
1 0.78 0.91 0.84 58
accuracy 0.83 118
macro avg 0.84 0.83 0.83 118
weighted avg 0.84 0.83 0.83 118
看看不同 λ \lambda λ 的决策边界
def draw_boundary(power, l): # 画图
density = 1000
threshhold = 2 * 10**-3
final_theta = feature_mapped_logistic_regression(power, l)
x, y = find_decision_boundary(density, power, final_theta, threshhold)
df = pd.read_csv('ex2data2.txt', names=['test1', 'test2', 'accepted'])
sns.lmplot('test1', 'test2', hue='accepted', data=df, size=6, fit_reg=False, scatter_kws={"s": 100})
plt.scatter(x, y, c='R', s=10)
plt.title('Decision boundary')
plt.show()
def feature_mapped_logistic_regression(power, l): # 一个函数获取最有的theta...
df = pd.read_csv('ex2data2.txt', names=['test1', 'test2', 'accepted'])
x1 = np.array(df.test1)
x2 = np.array(df.test2)
y=np.array(df.iloc[:, -1])
X = feature_mapping(x1, x2, power, as_ndarray=True)
theta = np.zeros(X.shape[1])
res = opt.minimize(fun=regularized_cost,
x0=theta,
args=(X, y, l),
method='TNC',
jac=regularized_gradient)
final_theta = res.x
return final_theta
def find_decision_boundary(density, power, theta, threshhold):
t1 = np.linspace(-1, 1.5, density)
t2 = np.linspace(-1, 1.5, density) # 两个等差数组
cordinates = [(x, y) for x in t1 for y in t2]
x_cord, y_cord = zip(*cordinates) # 这画到坐标轴的话应该是一个实心矩形
mapped_cord = feature_mapping(x_cord, y_cord, power) # this is a dataframe
# 映射后是不是就变成了一个圆形了。。。1000000 rows × 28 columns
inner_product = mapped_cord.values @ theta # theta 28*1
# 这下面我是真的看不懂了。。。。这个阈值还有上面的 -1-1.5 怎么选的。。。
decision = mapped_cord[np.abs(inner_product) < threshhold]
return decision.f10, decision.f01
#寻找决策边界函数
draw_boundary(power=6, l=1) #lambda=1
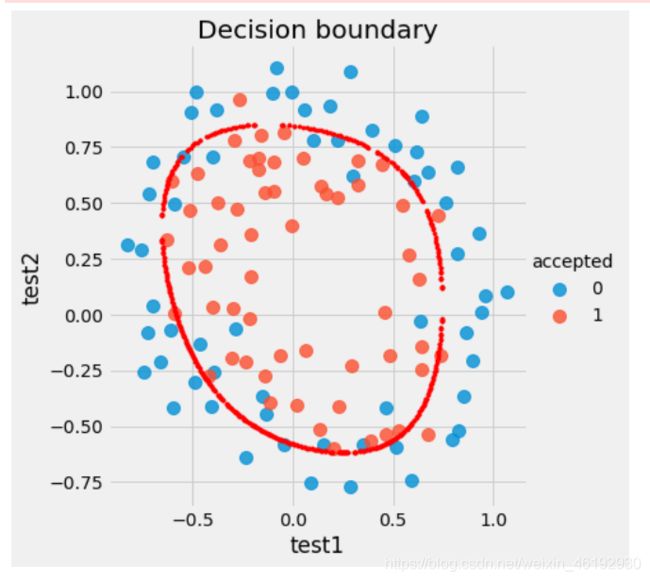
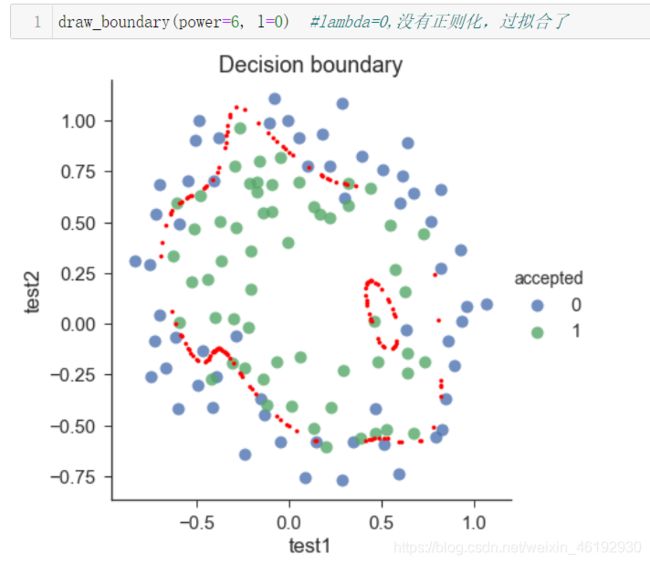
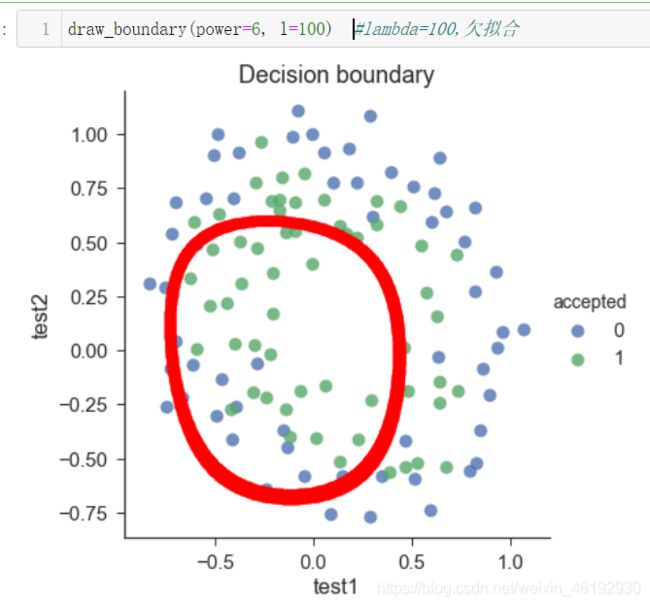
高级的
现在的我连调参侠都不配啊。。。。。
from sklearn import linear_model#调用sklearn的逻辑回归包
model = linear_model.LogisticRegression(penalty='l2', C=1.0)
model.fit(X2, y2.ravel())
model.score(X2, y2)
>>> 0.6610169491525424 # 不会调参,所以正确率不高。。。
好难啊,,,,整整看了三天。。。