找钱问题（记忆化搜索）

1. 问题描述：

给定数组arr{1，2，5}，arr中所有的值都为正数而且不重复，每个值代表一种面值的货币，每种面值的货币可以使用任意张，再给定一个整数aim代表要找的钱数，求换钱有多少种方法（aim大于0且不超过1000）

2. 思路分析：

① 分析题目可以知道这是一种不知道可能性的题目，需要进行试探，也就是需要尝试出所有可能的结果才可以得到最终的答案，所以一开始我们可以使用暴力的方法来解决的，可以这样想，因为每一种面值的钱的数目是可以拿任意张，所以我们对于每一种面值的分别拿取0，1，2...张直到不能够拿取了，所以对于每一种面值的钱都可以这样拿取，对于拿取相应张数的钱之后剩下的钱也是这样拿取，所以这里蕴含了递归的思想，对于问题进行了相同办法的求解，并且问题规模是在在一步步缩小的，所以可以写出以下的递归的代码

② 对于递归求解的方法，我们可以在求解的过程中使用集合数据结构来记录其中的中间过程，这样我们在找到满足条件的答案的时候可以将结果进行输出这样可以在小范围内检验答案是否是正确的，需要注意的一个问题是使用集合数据结构进行记录的时候在递归调用前进行结果的记录，在当前的递归调用结束之后对其进行回溯，也就是需要删除这一次记录的结果，因为我是在尝试这种的方案的可能性，尝试完这种可能之后我需要将这次记录在集合中的结果删除掉，以便尝试其他的结果，删除之后这样记录的中间结果才是正确的

3. 代码如下：

import java.util.ArrayList;
import java.util.List;
import java.util.Scanner;
public class Main {
	static List rec = new ArrayList();
	public static void main(String[] args) {
		int arr[] = {1, 2, 5};
		Scanner sc = new Scanner(System.in);
		int aim = sc.nextInt();
		int res = solve(arr, aim, 0);
		System.out.println(res);
		sc.close();
	}

	private static int solve(int[] arr, int aim, int index) {
		if(arr == null) {
			return 0;
		}
		if(aim == 0) {
			for(int i = 0; i < rec.size(); ++i){
				System.out.print(rec.get(i));
			}
			System.out.print("\n");
			return 1;
		}
	
		int t = 0;
		for(int i = 0; index < arr.length && i * arr[index] <= aim; ++i){
			String s = "";
			for(int j = 0; j < i; j++){
				s += arr[index] + " ";
			}
			rec.add(s);
			t += solve(arr, aim - i * arr[index], index + 1);
			rec.remove(rec.size() - 1);
		}
		return t;
	}
}

③ 上面的递归过程是没有进行任何优化的，对于问题进一步分析我们可以知道，假如当前有一种方案是我之前已经拿了1张5元，0张2元和1张5元的方案，但是在递归求解的过程中我尝试拿了0张1元，1张2元，而且在拿完0张1元，1张2元之后往下进行递归的时候与原来递归过程中的index与aim是一样的，这个时候就存在了重复子问题的求解了，因为往下进行递归的时候这两种方案求解的结果都是一样的，假如数据规模再大一点的时候那么耗费的时间是非常多的

④ 怎么样解决这个问题呢？我们可以采用记忆化的方法来解决子问题的重复求解，正是因为之前求解过，我才不用再一次进行求解，所以可以在求解的过程中使用数组来记录中间结果，当我们发现之前求解过了那么直接将之前记录的结果返回即可，这样可以大大减少重复求解的时间，这也是我们常说的使用空间换取时间的方法，但是具体怎么样做呢？分析题目可以知道当我们的方法中的index与aim是一样的时候那么往下递归就属于重复求解了，所以可以定义一个二维数组来表示，在递归之前进行判断之前是否求解过，并且需要注意一个边界的问题，因为我们需要判断的是往下递归是否会造成重复求解，所以在index + 1的时候需要判断数组是否越界的问题，在返回结果之前将结果记录在对应的二维数组中即可，然后进行返回

⑤ 不能够使用map来进行记录，因为map是一个键对应一个值而我们是两个变量对应一个值所以不能够使用map来记录，这其中涉及到如何判断重复子问题并且记录求解的中间结果，我们知道重复子问题是两种相同的状态下往下求解的所以求解的过程是一模一样的，所以造成了重复求解，具体来说就是方法中的某些变化的参数是一样的，当方法中这些变化的参数是一样的时候那么就会造成重复求解，所以这个也是很好进行判断的，就像这道题目来说当我拿取完之后index与aim是一样的时候往下递归假如之前可能求解过了那么将记录的结果直接返回即可

⑥ 在使用二维数组记录中间求解过的结果的时候，发现下面两种写法的耗时差别也是非常大的，第一种的话数据量大的时候也会非常耗时，第二种的话求解在1000之内的数据耗时非常短

可以发现第二种是先判断之前是否求解过然后再决定是否递归下去，而第一种是先递归下去然后再判断是否之前求解过，可能在往下递归判断的时候耗时比较大，所以使用第二种方法比较好

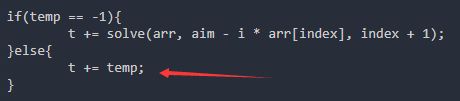
⑦ 在发现之前已经求解过之后需要加上之前的那个值最后才进行返回：

下面是对应的两种写法的代码（使用999来测试数据知道耗时长短了）：

1）

import java.util.ArrayList;
import java.util.List;
import java.util.Scanner;
public class Main {
	static int map[][] = new int[3][1000];
	public static void main(String[] args) {
		int arr[] = {1, 2, 5};
		Scanner sc = new Scanner(System.in);
		int aim = sc.nextInt();
		int res = solve(arr, aim, 0);
		System.out.println(res);
		sc.close();
	}

	private static int solve(int[] arr, int aim, int index) {
		if(aim == 0) {
			return 1;
		}
		if(arr == null || index == arr.length) {
			return 0;
		}
		if(map[index][aim] != 0) return map[index][aim];
		int t = 0;
		for(int i = 0; i * arr[index] <= aim; ++i){
			t += solve(arr, aim - i * arr[index], index + 1);
		}
		map[index][aim] = t;
		return t;
	}
}

2）

import java.util.ArrayList;
import java.util.Arrays;
import java.util.List;
import java.util.Scanner;
public class Main {
	static int map[][] = new int[3][1000];
	public static void main(String[] args) {
		int arr[] = {1, 2, 5};
		for(int i = 0; i < 3; ++i){
			Arrays.fill(map[i], -1);
		}
		Scanner sc = new Scanner(System.in);
		int aim = sc.nextInt();
		int res = solve(arr, aim, 0);
		System.out.println(res);
		sc.close();
	}

	private static int solve(int[] arr, int aim, int index) {
		if(aim == 0) {
			return 1;
		}
		if(arr == null || index == arr.length) {
			return 0;
		}
		int t = 0;
		for(int i = 0; i * arr[index] <= aim; ++i){
			int temp = -1;
			if(index + 1 < arr.length){
				temp = map[index + 1][aim - i * arr[index]];
			}
			if(temp == -1){
				t += solve(arr, aim - i * arr[index], index + 1);
			}else{
				t += temp;
			}
		}
		map[index][aim] = t;
		return t;
	}
}