吃瓜教程|Task5(阅读西瓜书第6章)
文章目录
-
- 1 间隔与支持向量
- 2 对偶问题
-
- 2.1 SMO
- 3 核函数
- 4 软间隔与正则化
- 5 支持向量回归
- 6 核方法
1 间隔与支持向量
给定训练样本集D,分类学习最基本的想法就是基于训练集D在样本空间中找到一个划分超平面,将不同类别的样本分开。
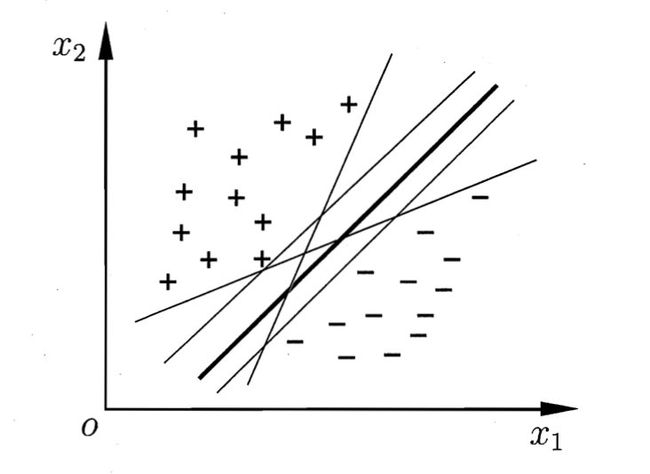
直观上看,应该去找位于两类训练样本“正中间”的划分超平面,即如图所示中间的曲线,因为该划分超平面对训练样本局部扰动的“容忍”性最好,也就是说,该划分超平面所产生的分类结果是最鲁棒的,对未见事例的泛化能力最强。
超平面方程如下描述:

其中 ω \omega ω为法向量,决定了超平面的方向, b b b为位移项,决定了超平面 ( ω , b ) (\omega,b) (ω,b)与原点之间的距离。
样本空间中任意点 x x x到超平面 ( ω , b ) (\omega,b) (ω,b)的距离为:

假设超平面 ( ω , b ) (\omega,b) (ω,b)能将训练样本正确分类,则有:
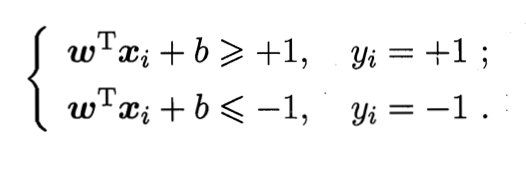
如图所示,距离超平面最近的几个训练样本可以使上式的等号成立,它们被称为“支持向量”,两个异类支持向量到超平面的距离之和为:
γ = 2 ∣ ∣ ω ∣ ∣ (n) \tag{n} \gamma = \frac{2}{||\omega||} γ=∣∣ω∣∣2(n)
它被称为“间隔”。

欲找到具有“最大间隔”的划分超平面,也就是要找到能满足分类公式中约束的参数 ω \omega ω和 b b b,使得 γ \gamma γ最大,即:
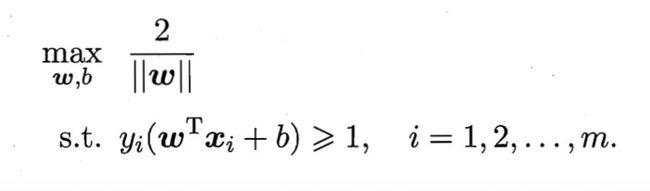
显然,为了最大化间隔,仅需要最大化 ∣ ∣ ω ∣ ∣ − 1 ||\omega||^{-1} ∣∣ω∣∣−1,这等价于最小化 ∣ ∣ ω ∣ ∣ 2 ||\omega||^{2} ∣∣ω∣∣2.于是,上式可以重写为:
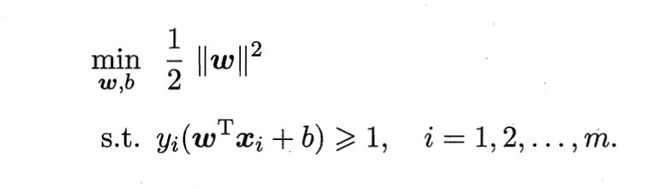
这就是支持向量机(SVM)的基本型。
2 对偶问题
对于上面支持向量机的最小化问题,本身是一个凸二次规划问题,可以直接用现成的优化计算包求解,也可以转化为对偶问题求解。
对每条约束添加拉格朗日乘子 a i > = 0 a_i>=0 ai>=0,则该问题的拉格朗日函数可写为:

令 L ( w , b , a ) L(w,b,a) L(w,b,a)对 w w w和 b b b的偏导为零可得:
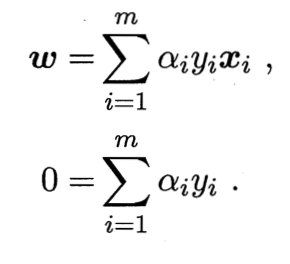
将上式代入 L L L函数中,再考虑零等式的约束,就得到基本型的对偶问题:
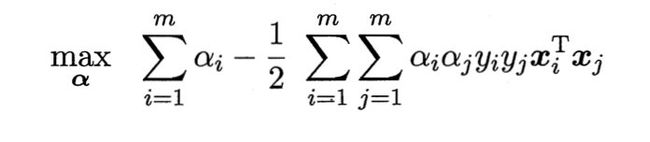

解出 α \alpha α后,求出 w w w与 b b b即可得到模型:

从对偶问题解出的 α i \alpha_i αi是 L L L函数的拉格朗日乘子,它恰对应着训练样本 ( x i , y i ) (x_i, y_i) (xi,yi),注意到基本型的式子中有不等式约束,因此上述过程需满足KKT条件,即要求:
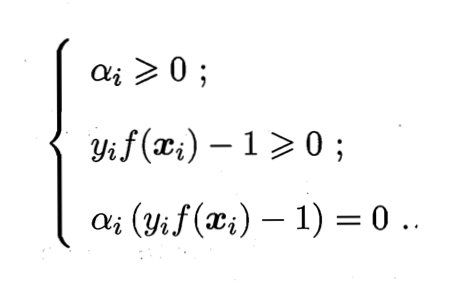
于是,对任意训练样本 ( x i , y i ) (x_i, y_i) (xi,yi),总有 α i = 0 \alpha_i = 0 αi=0或者 y i f ( x i ) = 1 y_if(x_i) = 1 yif(xi)=1.若 α i = 0 \alpha_i = 0 αi=0,则该样本将不会在式的求和中出现,也就不会对 f ( x ) f(x) f(x)有任何影响;若 α i > 0 \alpha_i > 0 αi>0,则必有 y i f ( x i ) = 1 y_if(x_i) = 1 yif(xi)=1,所对应的样本点位于最大间隔边界上,是一个支持向量。这显示出支持向量机的一个重要性质:训练完成后,大部分的训练样本都不需要保留,最终模型仅与支持向量有关。
为了求解对偶问题,首先考虑该问题是二次规划问题,可以使用通用的二次规划算法求解,但是该问题的规模正比于训练样本数,这会在实际任务中造成很大的开销。为了避开这个障碍,人们通过利用问题本身的特性,提出了很多高效算法,SMO就是其中一个著名的代表。
2.1 SMO
SMO的基本思路是先固定 α i \alpha _i αi之外的所有参数,然后求 α i \alpha _i αi上的极值。由于存在约束 ∑ i = 1 m α i y i = 0 \sum^m_{i=1}\alpha_iy_i = 0 ∑i=1mαiyi=0,若固定 α i \alpha _i αi之外的其他变量,则 α i \alpha _i αi可由其他变量导出。于是,SMO每次选择两个变量 α i \alpha _i αi和 α j \alpha _j αj,并固定其他参数。这样,在参数初始化后,SMO不断执行如下两个步骤直至收敛:
- 选取一对需更新的变量 α i \alpha _i αi和 α j \alpha _j αj
- 固定 α i \alpha _i αi和 α j \alpha _j αj以外的参数,求解对偶式获得更新后的 α i \alpha _i αi和 α j \alpha _j αj
注意到只需要选取的 α i \alpha _i αi和 α j \alpha _j αj中有一个不满足KKT条件,目标函数就会在迭代后减小.直观来看,KKT条件违背的程度越大,则变量更新后可能导致的目标函数减幅越大.于是,SMO先选取违背KKT条件程度最大的变量。第二个变量应该选择一个使目标函数减小最快的变量,但由于比较各变量所对应的目标函数减幅的复杂度过高,因此SMO采用了一个启发式:使选取的两变量所对应样本之间的间隔最大。一种直观的解释是,这样的两个变量有很大的差别,与对两个相似的变量进行更新相比,对它们进行更新会带给目标值更大的变化。
SMO算法之所以高效,恰由于在固定其他参数后,仅优化两个参数的过程能做到非常高效。具体来说,仅考虑 α i \alpha _i αi和 α j \alpha _j αj时,式子的不等式约束可以重写为:

其中:

是使 ∑ i = 1 m α i y i = 0 \sum^m_{i=1}\alpha_iy_i = 0 ∑i=1mαiyi=0成立的常数。用:
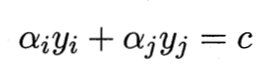
消去对偶式中的变量 α j \alpha _j αj,则得到一个关于 α i \alpha _i αi的单变量二次规划问题,仅有的约束是 α i > = 0 \alpha _i >= 0 αi>=0。不难发现,这样的二次规划问题具有闭式解,于是不必调用数值优化算法即可高效地计算出更新后的 α i \alpha _i αi和 α j \alpha _j αj。
那么如何确定偏移项b呢?注意到对任何支持向量 ( x i , y i ) (x_i, y_i) (xi,yi)都有 y i f ( x i ) = 1 y_if(x_i) = 1 yif(xi)=1,即:
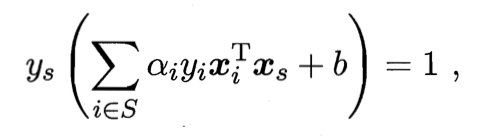
其中 S = { i ∣ α i > 0 , i = 1 , 2 , . . . , m } S = \{i|\alpha_i > 0,i = 1, 2,...,m\} S={i∣αi>0,i=1,2,...,m}为所有支持向量的下标集。理论上,可选取任意支持向量并通过求解上式获得b,但现实任务中常采用一种更鲁棒的做法:使用所有支持向量求解的平均值:

3 核函数
之前讨论的都是线性可分的训练样本,现在讨论线性不可分问题。

对这样的问题,可以将样本从原始空间映射到一个更高维的特征空间,使得样本在这个特征空间内线性可分。例如在上图中,若将原始的二维空间映射到一个合适的三维空间,就能找到一个合适的划分超平面。幸运的是,如果原始空间是有限的,即属性数有限,那么一定存在一个高维特征空间使样本可分。
令 φ ( x ) \varphi(x) φ(x)表示将 x x x映射后的特征向量,于是,在特征空间中划分超平面所对应的模型可表示为:

其中 w w w和 b b b是模型参数,类似线性可分问题,有:
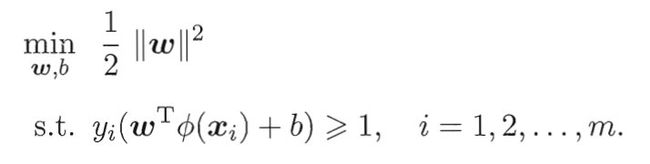
其对偶问题是:
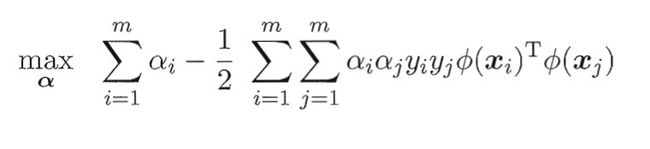
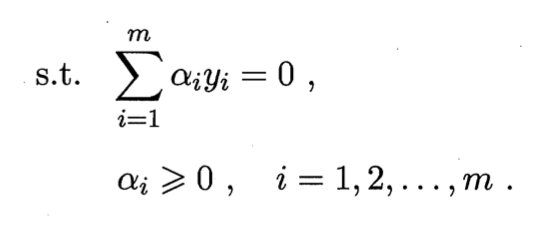
求解该问题涉及到计算 φ ( x i ) T φ ( x j ) \varphi(x_i)^T\varphi(x_j) φ(xi)Tφ(xj),这是样本 x i x_i xi与 x j x_j xj映射到特征空间之后的内积。由于特征空间维数可能很高,甚至可能是无穷维,因此直接计算 φ ( x i ) T φ ( x j ) \varphi(x_i)^T\varphi(x_j) φ(xi)Tφ(xj)通常是困难的。为了避开这个障碍,可以设想这样一个函数:

即 x i x_i xi与 x j x_j xj在特征空间的内积等于它们在原始样本空间中通过函数 k ( ⋅ , ⋅ ) k(·,·) k(⋅,⋅)计算的结果。有了这样的函数,我们就不必直接去计算高维甚至无穷维特征空间中的内积,于是对偶式可以重写为:

求解后即可得到:

这里的函数 k ( ⋅ , ⋅ ) k(·,·) k(⋅,⋅)就是“核函数”,上式显示出模型最优解可通过训练样本的核函数展开,这一展式亦称为“支持向量展式”。
显然,若已知合适映射 ϕ ( ⋅ ) \phi(·) ϕ(⋅)的具体形式,则可写出核函数 k ( ⋅ , ⋅ ) k(·,·) k(⋅,⋅)。但在现实任务中我们通常不知道 ϕ ( ⋅ ) \phi(·) ϕ(⋅)是什么形式,那么,合适的核函数是否一定存在呢?什么样的函数能做核函数呢?有下面的定理:
核函数定理:令 χ \chi χ为输入空间, k ( ⋅ , ⋅ ) k(·,·) k(⋅,⋅)是定义在 χ × χ \chi \times \chi χ×χ上的对称函数,则 k k k是核函数当且仅当对于任意数据 D = { x 1 , x 2 , . . . , x m } D = \{x_1,x_2,...,x_m\} D={x1,x2,...,xm},“核矩阵”K是半正定的:
定理表明,只要一个对称函数所对应的核矩阵半正定,它就能作为核函数使用。事实上,对于一个半正定核矩阵,总能找到一个与之对应的映射 ϕ \phi ϕ.换言之,任何一个核函数都隐式地定义了一个称为“再生核希尔伯特空间”的特征空间。
但在不知道特征映射的形势下,我们不知道什么样的核函数是合适的,而核函数也仅是隐式的定义了这个特征空间。于是,“核函数选择”成为支持向量机的最大变数。若核函数选择不合适,则意味着将样本映射到了一个不合适的特征空间,很可能导致性能不佳。

此外,还可通过函数组合得到,例如:
- 若 k 1 k_1 k1和 k 2 k_2 k2为核函数,则对于任意正数 γ 1 、 γ 2 \gamma_1、\gamma_2 γ1、γ2,其线性组合
γ 1 k 1 + γ 2 k 2 \gamma_1k_1 + \gamma_2k_2 γ1k1+γ2k2
也是核函数;
- 若 k 1 k_1 k1和 k 2 k_2 k2为核函数,则核函数的直积
k 1 ⊗ k 2 ( x , z ) = k 1 ( x , z ) k 2 ( x , z ) k_1\otimes k_2(x, z) = k_1(x, z)k_2(x, z) k1⊗k2(x,z)=k1(x,z)k2(x,z)
也是核函数;
- 若 k 1 k_1 k1为核函数,则对于任意函数 g ( x ) g(x) g(x),
k ( x , z ) = g ( x ) k 1 ( x , z ) g ( z ) k(x, z) = g(x)k_1(x, z)g(z) k(x,z)=g(x)k1(x,z)g(z)
也是核函数;
4 软间隔与正则化
问题:很难确定训练样本线性可分,即使使用核函数划分,也很难断定这个貌似线性可分的结果不是由于过拟合所造成的
引入:“软间隔”概念(允许支持向量机在一些样本上出错。

相比于硬间隔(所有样本均满足约束,即所有样本都必须划分正确),软间隔允许某些样本不满足约束:

当然,在最大化间隔的同时,不满足约束的样本应该尽可能少。于是,优化目标可写为:

其中 C > 0 C>0 C>0是一个常数, l 0 / 1 l_{0/1} l0/1是0/1损失函数
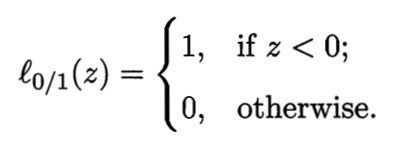
显然,当C为无穷大时,上式满足所有样本,当C取有限值时,式允许一些样本不满足约束。
然而, l 0 / 1 l_{0/1} l0/1非凸、非连续,数学性质不太好,使得优化目标不易直接求解。于是,人们通常用其他一些函数来替代 l 0 / 1 l_{0/1} l0/1,称为“替代函数”。替代损失函数一般具有较好的数学性质,如它们通常是凸的连续函数且是 l 0 / 1 l_{0/1} l0/1的上界。下图给出三种常用的替代损失函数:
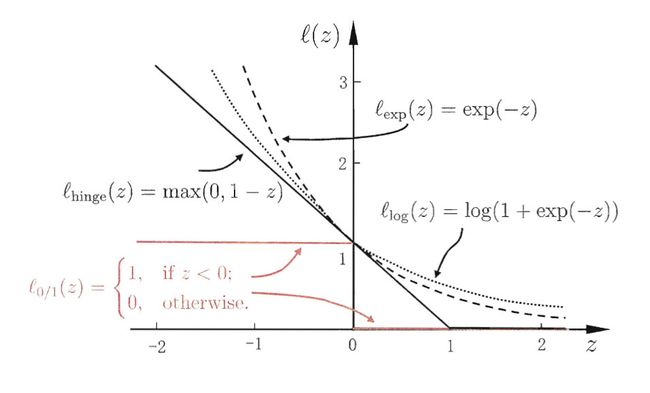
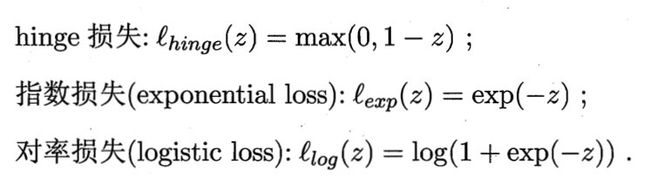
若采用hinge损失,则上式变为:

引入“松弛变量” ξ i ≥ 0 \xi_i \geq 0 ξi≥0,可将上式重写为:

这就是常用的“软间隔支持向量机”。
显然,上式中每个样本都有一个对于的松弛变量,用以表征该样本不满足约束的程度,但是,与对偶问题相似,这任然是一个二次规划问题,于是,可以通过拉格朗日乘子法可得到下式的拉格朗日函数。

其中 a i ≥ 0 , μ ≥ 0 a_i \geq 0, \mu \geq 0 ai≥0,μ≥0是拉格朗日乘子。

再代入原式可以得到对偶问题:
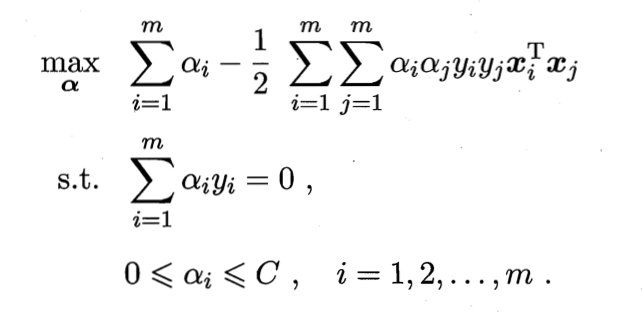
相比于硬间隔下的对偶问题,两者唯一的差别在于对偶变量的约束不同:前者是 0 ≤ a i ≤ C 0 \leq a_i \leq C 0≤ai≤C,后者是 0 ≤ a i 0 \leq a_i 0≤ai.于是,可采用硬间隔中同样的算法求解,得到同样的支持向量展开式。
对软间隔支持向量机,KKT条件要求:

软间隔支持向量机的一个重要性质:训练完成后,大部分的训练样本都不需要保留,最终模型仅与支持向量有关,通过采用hinge损失函数仍保持了稀疏性。
5 支持向量回归
回归问题:希望学得一个 f ( x ) = ω T x + b f(x) = \omega^Tx+b f(x)=ωTx+b回归模型,使得 f ( x ) f(x) f(x)与y尽可能接近,w和b是待确定的模型参数。
支持向量回归(Support Vector Regression,SVR)假设我们能容忍 f ( x ) f(x) f(x)与y之间最多有 ϵ \epsilon ϵ的偏差,即仅当 f ( x ) f(x) f(x)与y之间的差别绝对值大于 ϵ \epsilon ϵ时才计算损失。如下图所示,构建了一个宽度为 2 ϵ 2\epsilon 2ϵ的间隔带,若训练样本落入此间隔带,则认为是被预测正确的。
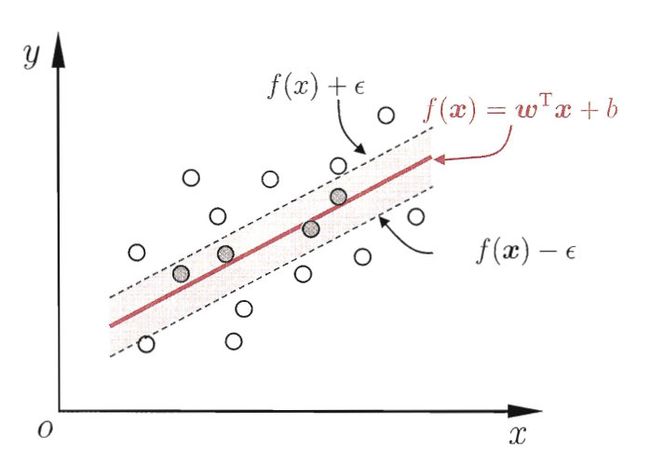
于是,SVR问题可形式化为:
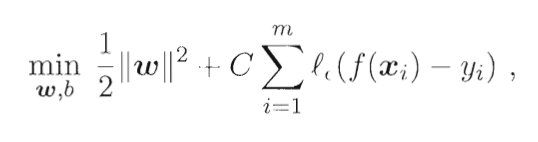
其中C为正则化常数, l ϵ l_\epsilon lϵ是 ϵ − \epsilon - ϵ−不敏感损失函数
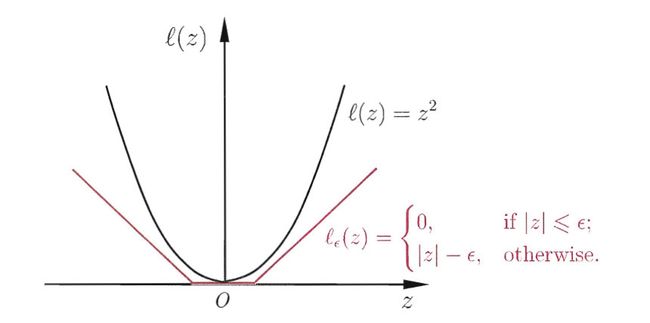
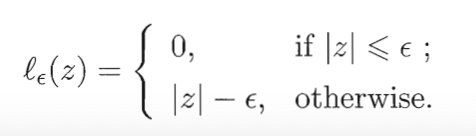
引入松弛变量 ξ i \xi_i ξi和 ξ i ^ \hat{\xi_i} ξi^可将上式重写为:


类似软硬间隔支持向量机方法,使用拉格朗日乘子法,得到对偶问题:

满足KKT条件

得到SVR的解形如:

6 核方法
后面回头学完再更新…
参考:
- 【吃瓜教程】《机器学习公式详解》(南瓜书)与西瓜书公式推导直播合集
- 《机器学习》.周志华