机器学习分类模型

分类模型总结

目录

一、介绍

1，分类

2，sklearn库

二，线性概率模型——逻辑回归

1，介绍

2，损失函数定义

3，连接函数的选取

3.1 Sigmoid函数

4、逻辑回归鸢尾花数据集

1，数据介绍

2 ，相关性分析

3，逻辑回归模型预测

5，注意点

一，知识点

二，涉及的sklearn

 三，SVM支持向量机

1，线性分类器

2，函数间隔与几何间隔

1，间隔与支持向量

2，函数间隔

 3，几何间隔

3，例题

4，实验

3，兼容软间隔

4，SVM鸢尾花数据集

5，SVM-核方法

1，核方法（kernel methods）

2，sklearn的SVM核方法

总结

---

前言

线性概率模型(Linear Probability Model)LPM

0-1回归，对于因变量为分类变量的情况，我们可以使用逻辑回归进行处理。把y看成事件发生的概率，y>=0.5发生，y<=0.5不发生。

一、介绍

1，分类

1）线性	属性非线性：特征转换（多项式回归） 全局性非线性：线性分类  激活函数（逻辑回归） 系数非线性：神经网络 ，感知机
2）全局性	线性样条回归：决策树
3）数据未加工	PCA，流形

线性分类：

硬分类	1）线性判别分析：fisher 2)  感知机
软分类	生成式：Gaussion Discriminal Analysis 判别式：Logistic Regression逻辑回归

2，sklearn库

from sklearn.linear_model import LogisticRegression
from sklearn.linear_model import Perceptron
from sklearn.neighbors import KNeighborsClassifier
from sklearn.tree import DecisionTreeClassifier
from sklearn.ensemble import AdaBoostClassifier
from sklearn.ensemble import StackingClassifier
from sklearn.naive_bayes import GaussianNB
from sklearn.svm import SVC #导入支持向量机分类选择器SVC
from sklearn.neural_network import MLPClassifier

二，线性概率模型——逻辑回归

1，介绍

利用上一章的多元线性回归模型进行回归。

写成向量乘积形式：

根据上一章讨论的内生性问题：只能取0或者1（回归系数估计出来不一致且有偏）

显然

预测值却可能出现或者的不现实情况

所以在给定的情况下，考虑的两点分布概率（伯努利分布）

事件	1	0
概率	p	1-p

           一般

被称为连接函数，它将解释变量x和被解释变量y连接起来

我们只需要保证是定义在[0,1]上的函数，就能保证

因为的值域是[0,1]可以理解为

 所以我们可以将理解为’y=1‘发生的概率

2，损失函数定义

或者

3，连接函数的选取

1）probit回归：取标准正太分布的累计密度函数

2）logistics逻辑回归 ：取Sigmoid函数

3.1 Sigmoid函数

sigmoid函数可微分

sigmoid函数处处连续

sigmoid的优点在于输出范围有限，所以数据在传递的过程中不容易发散。当然也有相应的缺点，就是饱和的时候梯度太小。

第二个有点就是导数比较容易计算，这样求梯度的时候就非常方便

sigmoid还有一个优点是输出范围为(0, 1)，所以可以用作输出层，输出表示概率。

def sigmoid(x):
	return 1/(1+np.exp(-x))

4、逻辑回归鸢尾花数据集

1，数据介绍

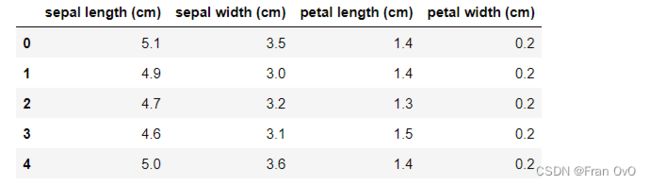
Iris也称鸢尾花卉数据集,是常用的分类实验数据集，由R.A. Fisher于1936年收集整理的。其中包含3种植物种类，分别是山鸢尾（setosa）变色鸢尾（versicolor）和维吉尼亚鸢尾（virginica），每类50个样本，共150个样本。

该数据集包含4个特征变量，1个类别变量。iris每个样本都包含了4个特征：花萼长度，花萼宽度，花瓣长度，花瓣宽度，以及1个类别变量（label）。我们需要建立一个分类器，分类器可以通过这4个特征来预测鸢尾花卉种类是属于山鸢尾，变色鸢尾还是维吉尼亚鸢尾。其中有一个类别是线性可分的，其余两个类别线性不可分，这在最后的分类结果绘制图中可观察到。

from sklearn.datasets import load_iris
iris = load_iris()
data = iris['data']
target = iris['target']
feature_names = iris['feature_names']
df = pd.DataFrame(data, columns=feature_names)
df.head()  # 查看前几行数据

2 ，相关性分析

import matplotlib.pyplot as plt
import seaborn as sns
plt.figure(figsize=(15,8))
mask = np.triu(np.ones_like(df.corr(), dtype=bool))
sns.heatmap(df.corr(), annot=True, mask=mask, vmin=-1, vmax=1)
plt.title('Correlation Coefficient Of Predictors')
plt.show()

 习惯做一下哈哈哈

3，逻辑回归模型预测

#训练逻辑回归
def fit(X, Y):
    theta = np.zeros(X.shape[1]) # 初始beta
    k = 0.1
    y=Y
    for i in range(1000):
        y_hat = 1 / (1 + np.exp(- X.dot(theta)))
        d = X.T.dot(y_hat - y)
        theta = theta - k*d
    return theta

from sklearn.linear_model import LogisticRegression
from sklearn.model_selection import cross_val_score
from sklearn.model_selection import train_test_split
train_X, test_X, train_Y, test_Y = train_test_split(data, target, train_size=0.7)
model = LogisticRegression(penalty='l2',solver='saga',max_iter=100, C=10)
model.fit(train_X,train_Y)
y_pred=model.predict(test_X)

accuracy = np.sum(test_Y == y_pred, axis=0) / len(test_Y)

#accuracy指标
accuracy = np.sum(test_Y == y_pred, axis=0) / len(test_Y)

5，注意点

一，知识点

1、逻辑回归的损失函数可以写成如下形式

         A、对

        B、错          

2、下列说法正确的是：

        A、损失值能够衡量模型在训练数据集上的拟合程度

        B、sigmoid函数不可导

        C、sigmoid函数的输入越大，输出就越大——（连续的单调递增函数）

        D、训练的过程，就是寻找合适的参数使得损失函数值最小的过程

3、sigmoid函数(对数几率函数)相对于单位阶跃函数有哪些好处？

        A、sigmoid函数可微分

        B、sigmoid函数处处连续

        C、sigmoid函数不是单调的

        D、sigmoid函数最多计算二阶导

4、逻辑回归的优点有哪些？

        A、需要事先对数据的分布做假设——（不同于线性回归，不需要线性假设，不需要考虑多重共线问题）

        B、可以得到“类别”的真正的概率预测

       C、可以用闭式解求解——不行，对于softmax的求解，没有闭式解法（高阶多项方程组求解），仍用梯度下降法，但是线性回归可以

        D、可以用现有的数值优化算法求解——（数值解）

Logistic Regression 虽然被称为回归，但其实际上是分类模型，并常用于二分类。Logistic Regression 因其简单、可并行化、可解释强深受工业界喜爱。

优点：

1. 实现简单，广泛的应用于工业问题上；

2. 分类时计算量非常小，速度很快，存储资源低；

3. 便利的观测样本概率分数；

4. 对逻辑回归而言，多重共线性并不是问题，它可以结合L2正则化来解决该问题；

5. 计算代价不高，易于理解和实现。

【机器学习】相关概念：闭式解，解析解，数值解

        解析解：因变量由自变量所表示的函数解析式，它是一个解析式，换句话说就是用参数表示的解。

        数值解：把各自的参数值自变量的值都带入到解析式中得到数值

        闭式解：解析解为一封闭形式〈closed-form〉的函数，因此对任一独立变量，我们皆可将其带入解析函数求得正确的相依变量。

像求解公式为

因此，解析解也被称为闭式解（closed-form solution）。

二，涉及的sklearn

from sklearn.linear_model import LogisticRegression

LogisticRegression(solver='lbfgs',max_iter=200,C=0.1)

         1，solver：{'newton-cg' ,  'lbfgs',  'liblinear',  'sag',  'saga'}，分别为几种优化算法。默认为liblinear；
        2，C：正则化系数的倒数，默认为 1.0 ，越小代表正则化越强，惩罚力度越强；

sigmoid:

def sigmoid(x):
	return 1/(1+np.exp(-x))

回归的评估指标acc:

#accuracy指标
accuracy = np.sum(test_Y == y_pred, axis=0) / len(test_Y)

 三，SVM支持向量机

 支持向量机support vector machine，故一般简称SVM，通俗来讲，它是一种二类分类模型，其基本模型定义为特征空间上的间隔最大的线性分类器，其学习策略便是间隔最大化，得到更好的决策边界。

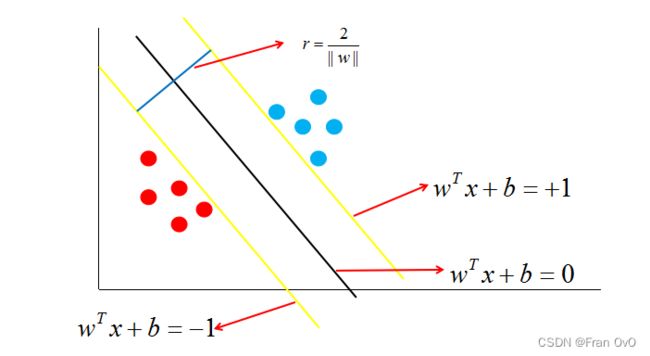
1. 能够很好的将样本划分
2. 离最近的样本点最远

它能够正确的将红点跟蓝点区分开来，而且，它还保证了对未知样本的容错率，因为它离最近的红点跟蓝点都很远，这个时候，再来一个数据，就不会出现之前黄色决策边界的错误了。

 

1，线性分类器

        给定一些数据点，它们分别属于两个不同的类，现在要找到一个线性分类器把这些数据分成两类。

        如果用x表示数据点，用y表示类别（y可以取1或者-1，分别代表两个不同的类），一个线性分类器的学习目标便是要在n维的数据空间中找到一个超平面（hyper plane），这个超平面的方程可以表示为（w 是垂直于超平面的一个向量，定义为法向量，而中的T代表转置）：

         Logistic回归目的是从特征学习出一个0/1分类模型，而这个模型是将特性的线性组合作为自变量，由于自变量的取值范围是负无穷到正无穷。

        因此，使用logistic函数（或称作sigmoid函数）将自变量映射到(0,1)上，映射后的值被认为是属于y=1的概率。                                

 从而，当我们要判别一个新来的特征属于哪个类时，只需求即可，若大于0.5就是y=1的类，反之属于y=0类。

2，函数间隔与几何间隔

1，间隔与支持向量

在样本空间中，决策边界可以通过如下线性方程来描述：

其中w=(w1​,w2​,..,wd​)为法向量，决定了决策边界的方向。b为位移项，决定了决策边界与原点之间的距离。显然，决策边界可被法向量和位移确定，我们将其表示为(w,b)。样本空间中的任意一个点x,到决策边界(w,b)的距离可写为：

假设决策边界(w,b)能够将训练样本正确分类，即对于任何一个样本点(xi​,yi​),若它为正类，即时，。若它为负类，即时，。

如图中，距离最近的几个点使两个不等式的等号成立，它们就被称为支持向量，即图中两条黄色的线。两个异类支持向量到超平面的距离之和为：

2，函数间隔

            在超平面确定的情况下，能够表示点x到距离超平面的远近，而通过观察的符号与类标记y的符号是否一致可判断分类是否正确，所以，可以用的正负性来判定或表示分类的正确性。于此，我们便引出了函数间隔（functional margin）的概念。

                                                   , 为函数间隔     

         而超平面(w，b)关于T中所有样本点(xi，yi)的函数间隔最小值（其中，x是特征，y是结果标签，i表示第i个样本），便为超平面(w, b)关于训练数据集T的函数间隔：

                                        

                      

 3，几何间隔

  假定对于一个点 x ，令其垂直投影到超平面上的对应点为 x0 ，w 是垂直于超平面的一个法向量，为样本x到超平面的距离，如下图所示： 

                                         

满足，是单位向量

又由于x0 是超平面上的点，满足 ，得。

 两边同时乘以   ,     得，又因为和，代入：

向量⃗分割超平面的距离是 

 为了得到的绝对值，令乘上对应的类别 y，        

即可得出几何间隔（用表示）的定义：

假使分类值由原来的 0 和 1 变成 -1 和 1 。

因此正例点的距离是：

负例点的距离恰好也是：

因此可设立模型目标：在保证的前提下，越大越好

3，例题

1，

计算两条向量的间隔r：

2,

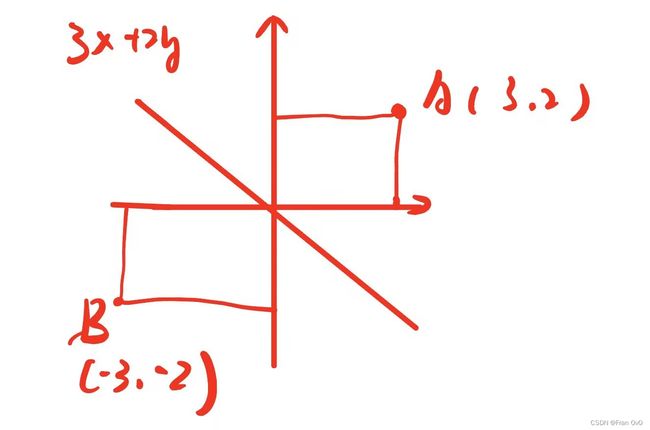
假设有两个样本点：(V,+1),(-V,-1)。其中，V=(3,2)，则使得间隔最大的决策边界为：

(ps:x为横坐标轴，y为纵坐标轴)

 

 

决策边界，那个样本点1和-1是类别

3，

有三个样本点：(x,+1),(y,+1),(z,-1)，超平面为:a+b=1。 其中,x=(3,0),y=(0,4),z=(0,0),则以下说法错误的为：

A、超平面能够将三个样本点按类别分隔开来
B、样本y到超平面的距离为3
C、样本z到超平面的距离的平方为0.5
D、离超平面距离最近的样本为z

4，实验

from sklearn.svm import LinearSVC
from sklearn.datasets import make_blobs
from sklearn.model_selection import train_test_split
from sklearn.metrics import accuracy_score
df = pd.read_csv('/data/bigfiles/2-4.csv')
X = np.array(df.iloc[:, :-1])
y = np.array(df.iloc[:, -1])

# 将 X, y 分成两部分，一部分用于训练，一部分用于测试。
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3)
# 1. 建立模型
model = LinearSVC(penalty='l2',loss='squared_hinge',C=1.0,
                  fit_intercept=True, max_iter=1000)

# 2. 训练模型
model.fit(X_train, y_train) # 训练
# 3. 测试预测
y_pred = model.predict(X_test) 
# 4. 测试评估
accuracy_score(y_pred, y_test) # 准确率

C = model.intercept_[0]#截距
A, B = model.coef_[0]#斜率
plt.grid(ls='--', color='lightgrey')
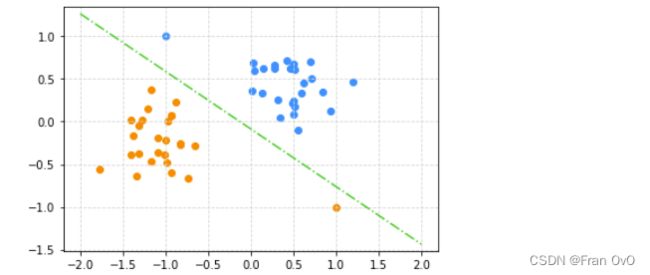
draw_dots()
draw_line(0, -C/B, -C/A, 0, -2, 2, 'limegreen', '-.')

 

参数：

1，C: 一个浮点数，罚项系数。C值越大对误分类的惩罚越大。
2，loss: 字符串，表示损失函数，可以为如下值：‘hinge’：此时为合页损失(标准的SVM损失函数)，‘squared_hinge’：合页损失函数的平方。
3，penalty: 字符串，指定‘l1’或者‘l2’，罚项范数。默认为‘l2’(他是标准的SVM范数)。

4，fit_intecept: 布尔值，如果为True，则计算截距，即决策树中的常数项，否则忽略截距。

5，max_iter: 一个整数，指定最大迭代数。
 

3，兼容软间隔

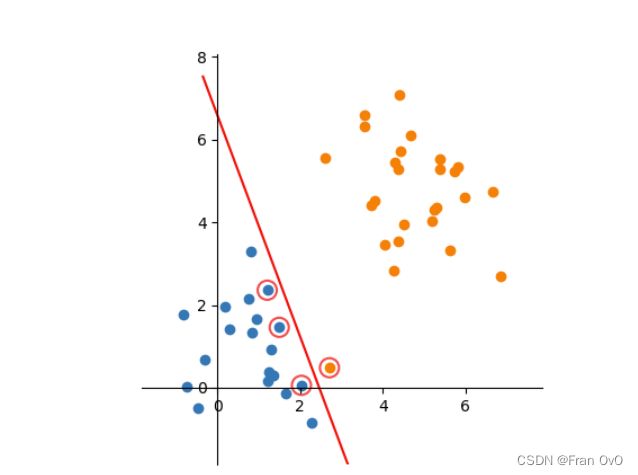
在实际问题中，总有可能偶尔出现异常数据，比如个别正标向量跑到了负标向量堆里去了，如果严格分类会造成一部分向量与决策面很近，甚至根本无法分界。要允许一部分数据进入内隔内侧，这种情况叫做软间隔

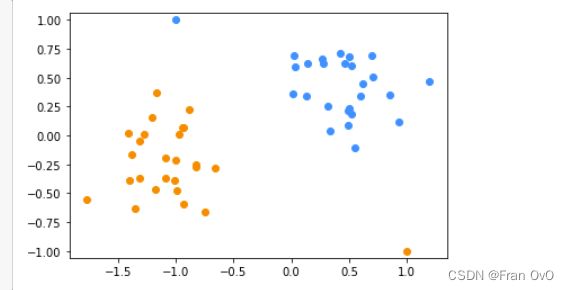
如下图所示：

这时为了容忍个别异常数据，提升模型鲁棒性，就叫做软间隔，实现下图分类效果：

# 将 X, y 分成两部分，一部分用于训练，一部分用于测试。
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3)
# 1. 建立模型

model = LinearSVC(penalty='l2',loss='squared_hinge',C=1.0,
                  fit_intercept=True, max_iter=1000)
# 2. 训练模型
model.fit(X_train, y_train) # 训练
# 3. 测试预测
y_pred = model.predict(X_test) 
# 4. 测试评估
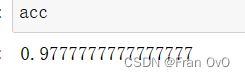
print(accuracy_score(y_pred, y_test)) # 准确率



C = model.intercept_[0]
A, B = model.coef_[0]
L = (A+B)**0.5
plt.grid(ls='--', color='lightgrey')
draw_dots()
draw_line(0, -C/B, -C/A, 0, -2, 2, 'limegreen', '-.')
draw_line(0, -(C+1)/B, -(C+1)/A, 0, -2, 2, 'springgreen', ':')
draw_line(0, -(C-1)/B, -(C-1)/A, 0, -2, 2, 'springgreen', ':')
plt.arrow(0, 0, A, B, color='black', head_width=0.1, length_includes_head=True)

4，SVM鸢尾花数据集

from sklearn.model_selection import cross_val_score
from sklearn.model_selection import train_test_split
from sklearn.svm import LinearSVC
import numpy as np
train_X, test_X, train_Y, test_Y = train_test_split(data, target, train_size=0.7)
model = LinearSVC()
model.fit(train_X,train_Y)
y_pred = model.predict(test_X)
acc = np.sum(test_Y==y_pred,axis=0)/len(test_Y)

5，SVM-核方法

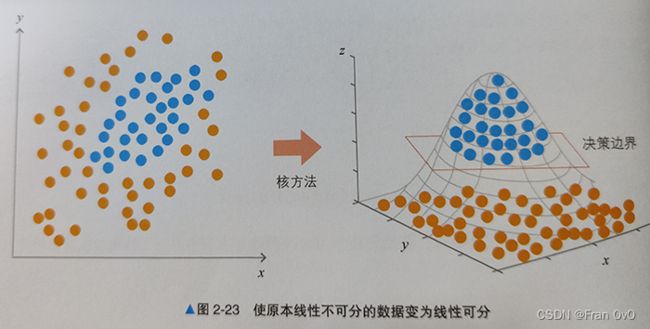
1，核方法（kernel methods）

        1.      在线性与非线性间架起一座桥梁，低维空间里面数据特征是非线性的，没法儿用线性方法解决，当数据特征映射到高维的时候，可以用线性方法解决。

        2.      通过巧妙地引进，避免了维数灾难，没有增加计算复杂度。

线性学习器相对于非线性学习器有更好的过拟合控制从而可以更好地保证泛化性能。

还有，很重要的一点是核方法还是实现高效计算的途径，它能利用核函数将非线性映射隐含在线性学习器中进行同步计算，使得计算复杂度与高维特征空间的维数无关。

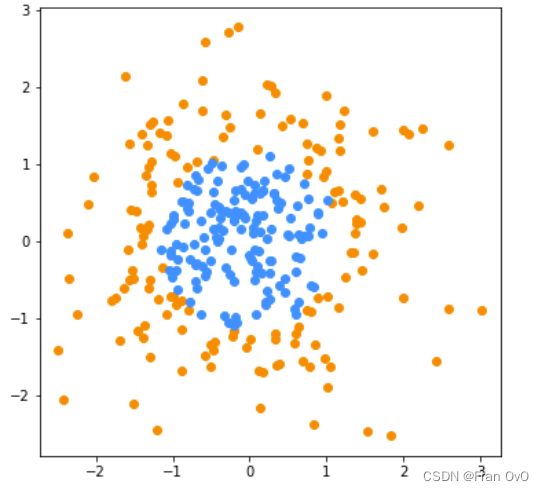
        3.       例子：用直线怎么分都不好分，怎么办？

提升到高维空间去

2，sklearn的SVM核方法

• kernel: 从这几个里选一个：{'linear', 'poly', 'rbf', 'sigmoid'}

• degree：当kernel是'poly'时使用，表示多项式次数

• gamma：当kernel是'poly'、'rbf'、'sigmoid'时使用，可以从这几项里选一个：{ 数值, 'scale', 'auto'}

• probability:启用概率估计， 启用之后会减缓拟合速度，但是拟合之后，模型能够输出各个类别对应的概率

from sklearn.svm import SVC   #这个才有核方法
model = SVC(kernel='linear', probability=True)   
# kernel: 从这几个里选一个：{'linear', 'poly', 'rbf', 'sigmoid'}
model.fit(X, y)
y_pred = model.predict(test_X)
acc = np.sum(test_Y==y_pred,axis=0)/len(test_Y)

acc=1强多了

predict返回的是一个预测的值，predict_proba返回的是对于预测为各个类别的概率

---

 

总结

提示：这里对文章进行总结：
例如：以上就是今天要讲的内容，本文仅仅简单介绍了pandas的使用，而pandas提供了大量能使我们快速便捷地处理数据的函数和方法。