期末复习笔记——图
一、图
1,完全图：
任意两个点都有一条边相连
无向完全图的边数：n(n-1)/2
有向完全图的边数：n(n-1)
2.稀疏图：
有很少边成弧的图（e 网：边/弧带权的图 邻接：有边相连的两个顶点之间的关系 任意两个顶点v,u间都存在v到u的路径 子图。。。。 无向图G的极大连通子图称为G的连通分量，有向图为强连通分量 极大（顶点数已经是达到最大了）连通子图：该子图是G连通子图，将G的任何不在孩子图中的顶点加入，子图就不连通了 强连通分量算法: Tarjan和Kosaraju ==》那么极小连通子图就是生成树啦 G=（V,E） ==>>Graph=(vertex,edge) V：顶点集 E：边集 有一个顶点表和一个邻接矩阵（就是一个二维数组）用来反映顶点之间的关系 假设G=(V，E)有n个顶点 顶点表 0 或者是网=》有权图 学习数据结构这门课，我最大收获就是代码规范性和可读性，要是以前，我都直接建个二维数组直接弄了； 可是一般的，邻接矩阵遇到大量数据就裂开了，所以一般我都不用OvO 邻接表可以说解决了上面的大部分问题，利用链表存储图。 当然，这种用链表实现的邻接表是真的复杂，所以之后我会分享两个不同方式实现的邻接表 链表实现就当基本功吧哈哈哈，知道邻接表长这个样子就行OvO 遍历方法： 链式前向星有一个head数组，几个结点就有几个数，然后是edge结构数组（表数组），存储三个数值 to,dis,next 那么head数组的下标就可以理解为from 刚开始head值都是-1当插入,from:1 to:2 dis:19 这样我们的head数组就能更新为edge数组的下标，edge的next也可以更新为head的值 再加入,from:1 to:3 dis:23重复上述操作 草稿而已，忽略字谢谢 这边我们利用链式前向星的遍历以及easyx画一张图的可视化： 过程很简单，就是画点和连线，和二叉树的动画一致 我们其实可以通过dfs和bfs的遍历，得到一棵无向生成树---极小连通子图 那如果要得到一棵权值和最小的生成树---最小生成树还需要用到算法 权值最小的边会包含在最小生成树中 那利用这个思想我们可以试想：贪心法，先给所有权值排个序，在从小到大连线，或者因为每个点都要包括，那就随便找个起点找与他相连接的最短权值； 这一种加点法就是kruskal算法，另一种点连边法就是prim算法 实质上算法思想就在上面大概提到了。 所以我们的目标就是一个点一个点找最小权值边，然后连起来，直到边数为n（顶点数）-1 我首先想到的是从第一个结点开始，遍历他的“邻居”，并更新存储权值数组dis的值，然后找到最小的权值对应的点再更新dis数组，同时遍历过的点用vis记录 然后我想可不可以用优先队列实现，因为他是把每个点与他连线的权值进行比较，那就可以将权值小的先出队 基于这个思想，我决定先不弄它（下次一定） 同时，我帮别人看代码的时候也顺带写了一下邻接矩阵的生成树 首先思想明确：先把权值排序，直接sort，然后从小到大连线 所以我翻了一下大一杭电算法课的视频和笔记，才发现，我把并查集给忘了，就是那个找祖先的，然后并在一起的“畅通工程” 为什么并查集可以实现不成环：如果一条边的两个顶点属于一个集合，右加入一条边不就成环了吗 所以思路清晰，贪心+并查集，下次再写 这里附加一段之前写的畅通工程hdu1233 同时，我之前链式前向星也写了很多算法，像迪杰斯特拉，强连通分量等等，好用的很 写的有点少还有什么拓扑排序，AOE都没整，那就真的下次一定。。。。3.顶点的度：与该顶点相关联的边的数目
4.连通图（强连通图）
5.连通分量（强连通分量）：
二、图的存储结构
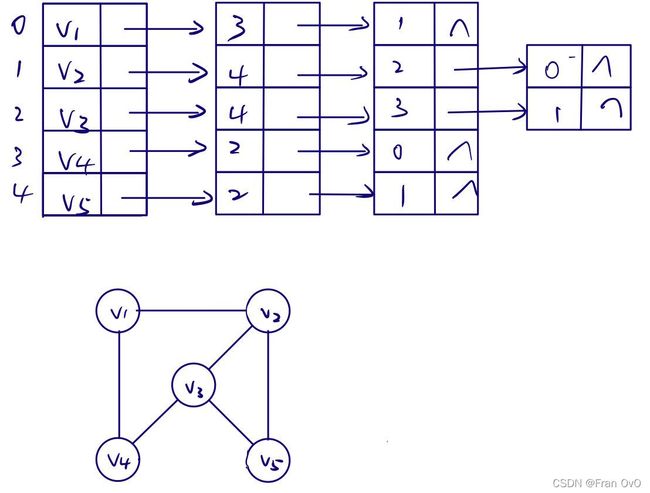
1.邻接矩阵
i
1
2
...
n-1
Vertex[i]
V1
V2
V3
Vn
![\text { B. } \operatorname{arcs}[\mathrm{i}][\mathrm{j}]=\left\{\begin{array}{l} 1 \\ 0 \end{array}\right.](http://img.e-com-net.com/image/info8/a159846d0c0a47ae880d77b574c83328.gif){kind=small}
![\text { A. } \operatorname{arcs}[\mathrm{i}][\mathrm{j}]=\left\{\begin{array}{l} W_{ij} \\ inf \end{array}\right.](http://img.e-com-net.com/image/info8/fe0c6746fedd4e47b452258e13b736fc.gif){kind=small}
const int inf = 0x7FFFFFFF;
const int MAXN = 100;
typedef char VerTexType;
typedef int Arctype;
typedef struct {
VerTexType vexs[MAXN << 2];
Arctype arcs[MAXN << 2][MAXN << 2];
int vexnum, arcnum;
}Graph;
void CreateUDN(Graph& G) {
cin >> G.vexnum >> G.arcnum;
for (int i; i < G.vexnum; ++i) {
cin >> G.vexs[i];
}
for (int i = 0; i < G.vexnum; i++) {
for (int j = 0; j < G.vexnum; j++) {
G.arcs[i][j] = inf;
}
}
int v1, v2, dis;
for (int k = 0; k < G.arcnum; k++) {
cin >> v1 >> v2 >> dis;
G.arcs[v1][v2] = dis;
G.arcs[v2][v1] = dis;
}
}
2.邻接表
2.1.1 STL的vector实现邻接表
struct edge {
int from, to, val;
};
const int MAXN = 100;
vector for (int i = 1; i <= n; i++)
{
for (int j = 0; j < MAP[i].size(); j++)
{
edge e = MAP[i][j];
cout << i << e.to << e.val << endl;
}
}2.1.2 链式前向星（邻接表的数组表示）有1说1，这个大一在杭电刘老师的算法班学到的图存储方法让我记忆深刻，不完全是他的这个高逼格的名字，还有他的方便以及便于理解（真的挺好理解的OvO）
struct node
{
int to;
int val;
int next;
}E[maxn << 2];
void add(int from, int to, int w)
{
cnt++;
E[cnt].to = to;
E[cnt].val = w;
E[cnt].next = head[from];
head[from] = cnt;
}
for (int i = 1; i <= n; i++) {
dis[i] = inf;
cin >> x >> y;
Vnode[i].data = { x,y };
Vnode[i].name = s[i-1];
head[i] = -1;
vis[i] = 0;
}
cin >> m;
for (int i = 0; i < m; i++)
{
int u, v, w;
cin >> u >> v >> w;
add(u+1, v+1, w);
add(v+1, u+1, w);
}void printG(int n) {
double xp, yp, xt, yt;
for (int node = 1; node <= n; node++){
setfillcolor(BLUE);
settextcolor(WHITE);
setbkmode(TRANSPARENT);
fillcircle(Vnode[node].data.x, Vnode[node].data.y, 20);
outtextxy(Vnode[node].data.x - 5, Vnode[node].data.y - 5, Vnode[node].name);
double x = Vnode[node].data.x;
double y = Vnode[node].data.y;
for (int i = head[node]; i!=-1 ; i = E[i].next) {
xt = Vnode[E[i].to].data.x, yt = Vnode[E[i].to].data.y;
setfillcolor(BLUE);
settextcolor(WHITE);
setbkmode(TRANSPARENT);
fillcircle(xt, yt, 20);
outtextxy(xt - 5, yt - 5, Vnode[E[i].to].name);
/* line(x, y, xt,yt);*/
/* Sleep(5000);*/
if (x < xt) {
for (xp = x, yp = y; xp <= xt;) {
xp += (xt - x) / 100, yp = ((y - yt) / (x - xt)) * (xp - x) + y;
line(x, y, xp, yp);
Sleep(15);
}
}
else if (x > xt) {
for (xp = x, yp = y; xp >= xt;) {
xp += (xt - x) / 100, yp = ((y - yt) / (x - xt)) * (xp - x) + y;
line(x, y, xp, yp);
Sleep(15);
}
}
settextcolor(RED);
setbkmode(TRANSPARENT);
char a[100];
_stprintf(a, _T("%d"), E[i].val);
outtextxy((xt+x)/2+10, (yt +y)/2+10, a);
}
}
}
3, 图的遍历
3.1深度优先DFS--递归，堆栈，类似树的先根遍历
3.2广度优先BFS--队列，类似树的层次遍历
4,最小生成树
4.1.1MST性质
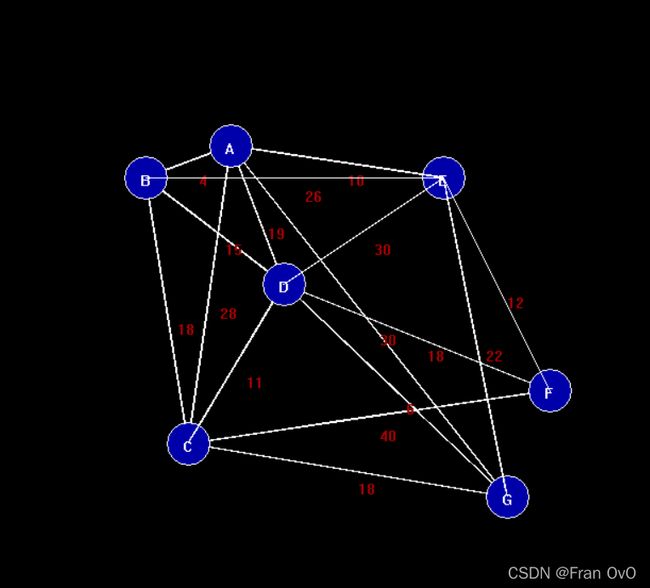
4.1.2prim算法
int Prim()
{
dis[1].dis = 1;
vis[1] = 1;
int now = 1;
char sumx[100];
string s="权值为:";
setfillcolor(YELLOW);
setlinecolor(GREEN);
settextcolor(BLACK);
setbkmode(TRANSPARENT);
fillcircle(Vnode[now].data.x, Vnode[now].data.y, 20);
outtextxy(Vnode[now].data.x - 5, Vnode[now].data.y - 5, Vnode[now].name);
Sleep(500);
for (int i = head[now]; i!=-1; i = E[i].next)
{
int u = E[i].to;
if (dis[u].dis > E[i].val) {
dis[u].dis = E[i].val;
dis[u].from = now;
dis[u].to = i;
}
}
int tot = 0;
int sum = 0;
while (tot < n - 1)
{
int old = now;
int MIN = inf;
for (int i = 1; i <= n; i++)
{
if (!vis[i] && dis[i].dis < MIN)
{
now = i;
MIN = dis[i].dis;
old = dis[i].from;
}
}
if (MIN == inf)return -1;
tot++;
sum += MIN;
Sleep(500);
vis[now] = 1;
setfillcolor(YELLOW);
settextcolor(BLACK);
setbkmode(TRANSPARENT);
fillcircle(Vnode[now].data.x, Vnode[now].data.y, 20);
outtextxy(Vnode[now].data.x - 5, Vnode[now].data.y - 5, Vnode[now].name);
double xt = Vnode[now].data.x, yt = Vnode[now].data.y, x = Vnode[old].data.x, y=Vnode[old].data.y;
setlinecolor(GREEN);
setlinestyle(PS_SOLID, 3);
line(x, y,xt, yt);
Sleep(600);
setfillcolor(YELLOW);
settextcolor(BLACK);
setbkmode(TRANSPARENT);
fillcircle(Vnode[now].data.x, Vnode[now].data.y, 20);
outtextxy(Vnode[now].data.x - 5, Vnode[now].data.y - 5, Vnode[now].name);
for (int i = head[now]; i!=-1; i = E[i].next)
{
int u = E[i].to;
if (vis[u] == 1)continue;
if (dis[u].dis > E[i].val) {
dis[u].dis = E[i].val;
dis[u].from = now;
dis[u].to = i;
}
}
_stprintf(sumx, _T("%d"), MIN);
if (tot == n - 1) {
s += sumx;
s += '=';
_stprintf(sumx, _T("%d"), sum);
s += sumx;
}
else {
s += sumx;
s += '+';
}
char c[100];
strcpy(c, s.data());
settextcolor(RED);
outtextxy(0, 400, c);
}
return sum;
}
struct edgenodes {
int from, to;
int dis;
};//用来保存加入lowcost的坐标
void Prim()//求图G中从vs顶点到达其余各顶点的最短路径
{
int dis[100];
char sumx[100];
//int v = 0;
string s = "权值为:";
int now = 0, old;
//v是顶点集，u是已经加入的顶点集
edgenodes lowcost[100];//最短边
int MIN;
int sum = 0;
int vis[100];//因为是加入点，所以要看到底有没有拜访过这个点，所以用vis记录有没有拜访过
for (int i = 0; i < G.vexnum; i++) {
lowcost[i].dis = INT_MAX;
vis[i] = 0;
}//规范一下先给他们初始化，最短边都为无穷，vis都没拜访过
//int closest[100];//最近点
//int i, j, k = 0;
//for (int i = 0; i < G.vexnum; i++)
//{
// lowcost[i] = G.arcs[now][i];
// closest[i] = now;
//}
vis[now] = 1;//这里就是说now已经拜访过了
for (int i = now; i < G.vexnum; i++)
{
if (G.arcs[now][i] < lowcost[i].dis) {
lowcost[i].dis = G.arcs[now][i];//因为记录的是最小边，如果现在的点和i点权值比记录的lowcost小，那就进来
dis[i] = lowcost[i].dis;
lowcost[i].from = now;
lowcost[i].to = i;
}
}
//这边意思是找个点第一个加入 顶点集u 中，像这里加的就是 第一个点 v=0
// 所以我把v改成now就是要加入的点,old是下次要加入的点
//然后找与v相连的点的权值，G.arcs[v][i]就是v到与他相连的点的权值
//
//
//这里我是让加入的点都变个色，就是每一个v加入u中，我就让他变成红色
setfillcolor(RED);
fillcircle(G.vexs[now].x, G.vexs[now].y, R);
//文字
settextcolor(BLACK);
setbkmode(TRANSPARENT);
outtextxy(G.vexs[now].x - 5, G.vexs[now].y - 5, G.vexs[now].data);//变色会改掉原有文字，所以再变一下
for (int i = 1; i < G.vexnum; i++)//vexnum-1遍遍历
{
//这边用old记入上次加入的顶点，目的是画图，就是等下要加入的点和旧点要进行连线
MIN = INT_MAX;
for (int j = 0; j < G.vexnum; j++)
{
if (!vis[j] && lowcost[j].dis < MIN&&lowcost[j].dis!= INT_MAX)//没拜访过，且这条边还比最小的小
{
MIN = lowcost[j].dis;
/*k = j*/;
now = j;//找到新的点，给它更新一下
old = lowcost[j].from;//这边用old记入上次加入的顶点，目的是画图，就是等下要加入的点和旧点要进行连线
}
}
sum += MIN;
//然后画出新的点
setfillcolor(RED);
fillcircle(G.vexs[now].x, G.vexs[now].y, R);
settextcolor(BLACK);
setbkmode(TRANSPARENT);
outtextxy(G.vexs[now].x - 5, G.vexs[now].y - 5, G.vexs[now].data);//变色会改掉原有文字，所以再变一下
//旧的点和新的点连线
setlinecolor(RED);
setlinestyle(PS_SOLID, 3);
line(G.vexs[now].x, G.vexs[now].y, G.vexs[old].x, G.vexs[old].y);
settextcolor(BLACK);
setbkmode(TRANSPARENT);
outtextxy(G.vexs[now].x - 5, G.vexs[now].y - 5, G.vexs[now].data);//画线也会改掉原有文字，所以再写一下
Sleep(600);
vis[now] = 1;//给新的点记录拜访过了
/* for (j = 0; j < G.vexnum; j++)
{
if (lowcost[j] != 0 && G.arcs[k][j] < lowcost[j])
{
lowcost[j] = G.arcs[k][j];
closest[j] = k;
}
}*/
//下面就是将更新一下和now相连的边的权值
for (int k = 0; k < G.vexnum; k++)
{
if (vis[k] == 1)continue;
if (G.arcs[now][k] < lowcost[k].dis) {
lowcost[k].dis = G.arcs[now][k];//因为记录的是最小边，如果现在的点和i点权值比记录的lowcost小，那就进来
lowcost[k].from = now;
lowcost[k].to = k;
dis[k] = lowcost[k].dis;
}
}
_stprintf(sumx, _T("%d"), MIN);
if (i == G.vexnum - 1) {
s += sumx;
s += '=';
_stprintf(sumx, _T("%d"), sum);
s += sumx;
}
else {
s += sumx;
s += '+';
}
char c[100];
strcpy(c, s.data());
settextcolor(RED);
outtextxy(0, 400, c);
}
}4.1.2krusal算法
这里注意：你连线要注意连上去会不会成环，所以你要判断，我这里刚开始是想用拓扑排序来判断的，但好像每加一条，就判断一下，有点那个。
#include