Python数学建模 多元线性回归

基于Python的数学建模

• Github仓库：Mathematical-modeling

生成回归数据

import numpy as np
from sklearn.datasets import make_regression
feature,target = make_regression(n_samples=100, n_features=5, n_informative=3, random_state=666)

多元线性回归

1. $y={\beta }_0+{\beta }_1{x}_1+\cdots +{\beta }_p{x}_p+ϵ$
2. 基本假设
   • 回归模型设定是正确的
   • 对于每个$x_j$,$0<j\le k$具有变异性。同时，样本量最少满足$n\ge k+1$，且$X_j$之间不存在多重共线性
   • 随机干扰项条件零均值$E(\mu |X)=0$
   • 随机干扰项条件同方差与序列不相关
   • 随机干扰项正态分布

多重共线性检验(方差膨胀因子VIF)

• $VI{F}_i=\frac{1}{1-R_i^2}$
• 其中$R_i$为第$i$个变量$X_i$与其他全部变量$X_j,(i=1,2,3,\cdots ,k;i\ne j)$的复相关系数；

复相关系数即可决系数$R^2$的算术平方根，也即拟合优度的算术平方根。
这个可决系数$R_i^2$是指用$X_i$做因变量，对其他全部$X_j,(i=1,2,3,\cdots ,k;i\ne j)$做一个新的回归以后得到的可决系数。

• $VIF$通常以10作为判断边界。
  • 当$VIF<10$,不存在多重共线性；
  • 当$10\le VIF<100$,存在较强的多重共线性；
  • 当$VIF\ge 100$, 存在严重多重共线性。

1. 多重共线性是普遍存在的，轻微的多重共线性问题可不采取措施。
2. 严重的多重共线性问题，一般可根据经验或通过分析回归结果发现。如影响系数符号，重要的解释变量t值很低。要根据不同情况采取必要措施。
3. 如果模型仅用于预测，则只要拟合程度好，可不处理多重共线性问题，存在多重共线性的模型用于预测时，往往不影响预测结果。

from statsmodels.stats.outliers_influence import variance_inflation_factor
# 输入变量
# exog：所有解释变量
# exog_idx：解释变量的columns标签
for i in range(feature.shape[1]):
    print("第{}个解释变量的VIF值为{}".format(i+1,variance_inflation_factor(feature,i)))

多重共线性处理

• 实际应用中，若存在多重共线性，需要消除多重共线性，不能直接建立多元线性回归模型；
• 待补充

变量间相关性分析

正态检验

• Pearson相关系数以及典型相关分析都要求样本数据满足正态分布的要求
• 因此首先对样本数据的正态分布进行检验
  • JB检验(大样本 n>30)
  • Shapior-wilk检验(小样本 3
  • KS检验(Kolmogorov-Smirnov)

from scipy import stats

print("样本的数据长度：",feature.shape[0])
# Statstic: 代表显著性水平
# P: 代表概率论与数理统计中的P值
for i in range(feature.shape[1]):
    jb_value,p = stats.jarque_bera(feature[:,i])
    if p < 0.05:
        judge = '拒绝原假设'
    else:
        judge = '接受原假设'
    print("第{}个变量的Test Statstic为{}, P值为:{}, {}".format(i,jb_value,p,judge))

Pearson相关系数

import pandas as pd

pd.DataFrame(feature).corr(method='pearson')

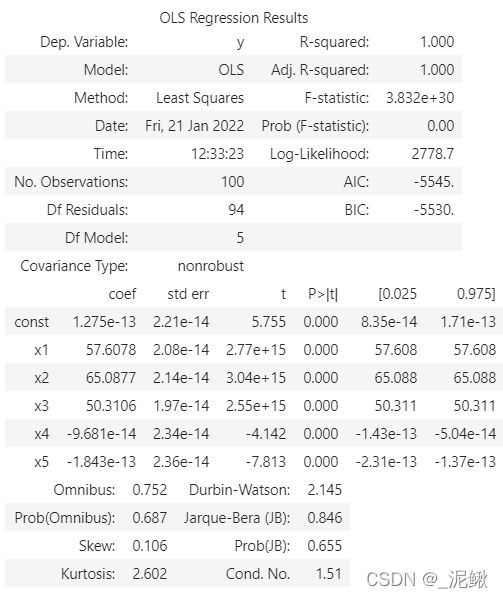
建立多元回归模型

拟合模型

• R-squared，即表示拟合优度$R^2$，用来衡量估计的模型对观测值的拟合程度。它的值越接近1说明模型越好;
• Adj.R-squared，即调整后的$R^2$，同时考虑了样本量$n$和回归中自变量的个数$k$的影响;
• F-statistic：方差分析
  • $H_0:$所有回归系数都等于零。$H_1:$所有回归系数不全为零。
  • 若Prob (F-statistic)即P值小于0.05，则拒绝原假设，认为多元线性回归模型总体显著。
  • 若$F>F_{\alpha }(K_n,-k-1)$，则接受原假设，认为多元线性回归模型总体不显著。
  • 若$F\le F_{\alpha }(K_n,-k-1)$，则拒绝原假设，认为多元线性回归模型总体显著。
• 单个变量的显著性检验：t统计量
  • 与F统计量类似，若P值小于0.05，则拒绝原假设，认为该自变量显著，对因变量解释性较强。

# 可以通过Scipy计算F统计量和T统计量
from scipy.stats import f,t
F_Theroy = f.ppf(q=0.95, dfn=5, dfd=10-5-1)
print('F: {}'.format(F_Theroy))
T_Theroy = t.ppf(q=0.975, df=100-5-1)
print('T: {}'.format(T_Theroy))

import statsmodels.api as sm

X = feature
Y = target 
X = sm.add_constant(X) # 添加截距项
model = sm.OLS(Y,X).fit()
model.summary()

#绘制最佳拟合线：标签用的是训练数据的预测值y_train_pred
y_pred = model.predict(X)
fig,ax = plt.subplots(figsize=(8,4))
ax.plot(Y,color='#00b0ff',label="Observations",linewidth=1.5)
ax.plot(y_pred,color='#ff3d00',label="Prediction",linewidth=1.5)
ax.legend(loc="upper left",fontsize=12)
ax.grid(alpha=0.6)
ax.tick_params(labelsize=14)

绘制拟合图

import matplotlib.pyplot as plt
y_pred = model.predict(X)
fig,ax = plt.subplots(figsize=(8,4))
ax.plot(Y,color='#00b0ff',label="Observations",linewidth=1.5)
ax.plot(y_pred,color='#ff3d00',label="Prediction",linewidth=1.5)
ax.legend(loc="upper left",fontsize=12)
ax.grid(alpha=0.6)
ax.tick_params(labelsize=14)

异方差检验

• 检验多元线性回归方差是否存在异方差

from statsmodels.stats.diagnostic import spec_white

X= feature
X=sm.add_constant(X) # 添加截距项
error = model.resid  #模型的残差
statistic,p,n = spec_white(error,X)
print("The test statistic: {};\n\
    P Value: {};\n\
        The degree of Freedom: {};".format(statistic,p,n))

自相关性检验

from statsmodels.stats.diagnostic import acorr_breusch_godfrey
lm, p_lm, f, p_f = acorr_breusch_godfrey(model)
print("Lagrange multiplier test statistic: {};\n\
    P Value-LM: {};\n\
        F Statistic: {};\n\
            P Value-F{}".format(lm, p_lm, f, p_f))