使用MMA解决拓扑优化问题的并行框架
使用MMA解决拓扑优化问题的并行框架
仅个人论文学习笔记。
本文的重点是用c++实现的完全并行拓扑优化框架(线性求解器和优化算法),将MMA(Method of Moving Asymptotes)优化算法并行化,作为代码的基本部分。
实现一个拓扑优化问题
在并行框架中实现任何给定的拓扑优化问题都遵循本节中介绍的两个步骤。该程序由图3所示的Stokes流优化问题举例说明。这里的目标是使压降最小化,受30%的体积限制以及出口1和2的质量流量限制。
虽然流问题不是一个多物理问题,但它需要定义两个状态场,velocity和pressure,因此具有与全耦合问题(如具有大带宽系统矩阵的鞍点系统)相同的特征。
实现的第一步是创建解决状态和优化问题所需的元素。这包括PDE的离散化以及优化问题的目标、约束和敏感性。在c++框架中,元素类遵循预定义的、通用的接口,即利用继承和虚拟方法的概念。用户只需定义与特定元素相关的方法,而其他方法可以留空。图3的例子问题可以很好地说明这一点。为了解决这个问题,总共需要写5类,即两个体积和三个边界条件条件对象。第一个体积元件单独解决流动问题,并用于进口和出口。这个元素只需要指定3个方法;read()从输入文件解析输入,SetDOF()设置dof, SetMat()计算并将元素贡献添加到全局切线矩阵中。第二个体积元素解决了设计域内的流动问题。除了前面提到的三种方法之外,这个元素还需要定义额外的优化方法,即返回对目标、约束和敏感度的贡献的方法。最后三个单元为边界单元,分别对应进口、出口和无滑移边界条件。这些元素的方法遵循与前面描述的两个方法相同的逻辑。
因此,在框架内实现PDE约束优化问题只需要用户能够将PDE问题以离散形式表示,例如有限元形式或任何其他具有空间局部性的方法,并提供目标、约束和灵敏度的表达式。用户不需要掌握并行通信和分区、网格和节点表、DOF编号、组装过程等知识。因此,尽管该框架不是为高级用途而设计的,例如Comsol Multiphysics,但实现一个新的物理或多物理问题的方法是类似的。实现的第二步也是最后一步是创建一个执行实际优化任务的驱动程序。驱动程序具有与所考虑问题的拓扑优化流程图相同的结构。对于Stokes流问题,流程图和驱动程序可以表述为
- 初始化问题参数并分配DOFs
- 声明矩阵、向量和优化结构,并为状态和伴随问题选择线性求解器(和预处理器)。
- 循环直到收敛:
- 组装并求解状态问题。
- 计算目标和约束条件。
- 求解伴随矩阵和计算灵敏度。
- 更新设计并检查收敛性。
- 结束
当然,驱动程序的实际实现需要多写几行代码,但总体结构如上所述。
MMA子问题的并行生成和求解
本节将介绍一个可以使用所提出的并行框架解决的一般优化问题。不等式约束优化问题可以表述为
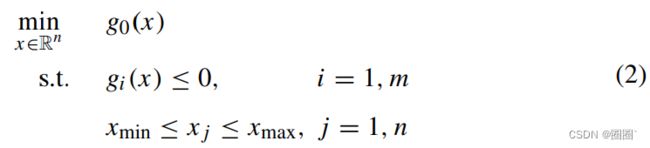 n 是设计变量的数量,m 是约束的数量。
n 是设计变量的数量,m 是约束的数量。
我们假设目标函数和约束函数 g0 和 gi 是光滑的、非线性的、非凸的。用(2)所述的形式直接解决问题是困难的。求解式(2)所给出的非线性规划问题的一种行之有效的方法是生成并求解一系列近似子问题。MMA中考虑了这种类型的解决策略。
MMA子问题
MMA的思想是解决一系列近似的子问题,而不是原来的非线性问题。这意味着(2)中的函数 g0(x) 和 gi(x) 是由一些适当的函数逼近的。为了得到一个数值上易于处理的优化问题,近似值必须是凸的。由于近似仅在展开点附近有效,因此必须重复生成和求解子问题的过程,从而产生解序列xk,其中 k 为迭代计数器。这个过程重复进行,直到满足指定的收敛条件。
在MMA中,近似是基于这类型的凸函数
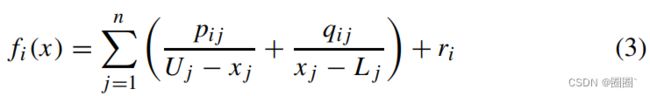 其中U和L分别是上渐近线和下渐近线,它们就是方法名称的(一半)。系数和渐近线,即pij, qij, ri, U, L,在每次迭代时都基于当前设计变量xk更新,在 xk 求函数值,即 g0(xk) 和 gi(xk),以及灵敏度∂g0(xk)/∂xj 和 ∂gi(xk)/∂xj。如果有的话,还会使用历史设计变量。Svanberg(1987)详细描述了MMA子问题系数的生成表达式。
其中U和L分别是上渐近线和下渐近线,它们就是方法名称的(一半)。系数和渐近线,即pij, qij, ri, U, L,在每次迭代时都基于当前设计变量xk更新,在 xk 求函数值,即 g0(xk) 和 gi(xk),以及灵敏度∂g0(xk)/∂xj 和 ∂gi(xk)/∂xj。如果有的话,还会使用历史设计变量。Svanberg(1987)详细描述了MMA子问题系数的生成表达式。
MMA子问题利用人工或“弹性”变量来确保子问题总是有一个可行的解决方案。下面用 yi≥0 表示弹性变量,从约束中减去弹性变量,并在目标中加上惩罚。
MMA子问题最常见的公式还包括一个额外的变量z,它可以用来解决非光滑问题,如最小-最大问题。在这里给出的实现中也包含了这样一个变量。
综上所述,MMA子问题可以表述为
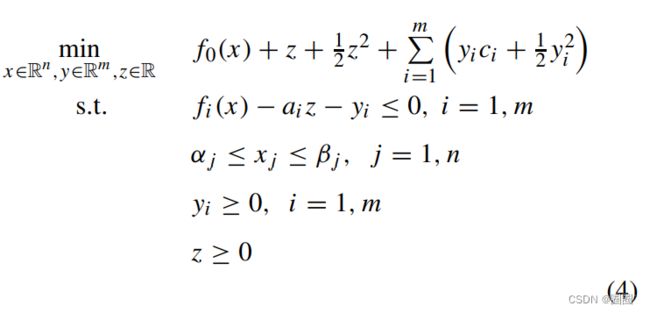 当用对偶方法来解决子问题时,z 和 yi 的二次项是必要的,但对于原始方法可以省略(例如Luenberger和Ye 2008)。
当用对偶方法来解决子问题时,z 和 yi 的二次项是必要的,但对于原始方法可以省略(例如Luenberger和Ye 2008)。
MMA子问题可以使用几种不同的方法来解决。在提出的c++框架中,我们实现了一个原始/对偶求解器和一个对偶求解器。原始/对偶求解器同时解决原始变量(即x, y和z)的子问题,以及约束对应的拉格朗日乘子集。拉格朗日乘数在这里被称为对偶变量(Andreasson et al. 2005)。对偶方法包括重写(4)中的优化问题为一个单独的拉格朗日乘数的问题。最后,应该注意的是,一旦开发出子问题求解器,就很容易实现Svanberg(2002)所描述的全局收敛MMA。
对偶求解器
在提出的优化框架中,使用内点法求解MMA子问题(4)的对偶问题。下面将展示这个子问题求解器的完整形式,以演示如何并行实现简单的MMA。构造求解器的第一步是获得(4)中MMA子问题的对偶。这是通过形成增广拉格朗日函数L来实现的。
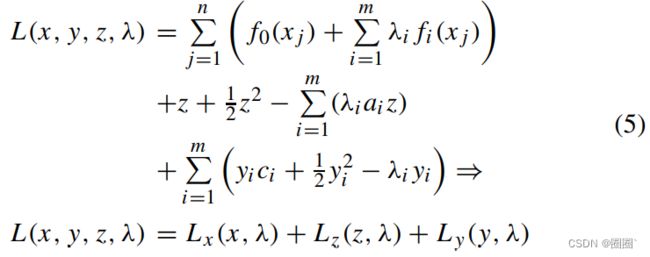 其中,这些项被组织起来说明子问题的可分性, λ i ≥ 0 , i = 1 , m λ_i ≥ 0,i = 1, m λi≥0,i=1,m 是非线性不等式约束的拉格朗日乘子。
其中,这些项被组织起来说明子问题的可分性, λ i ≥ 0 , i = 1 , m λ_i ≥ 0,i = 1, m λi≥0,i=1,m 是非线性不等式约束的拉格朗日乘子。
拉格朗日对偶 Ψ \Psi Ψ(λ)通过求解以下一系列简单的最小化问题而形成。
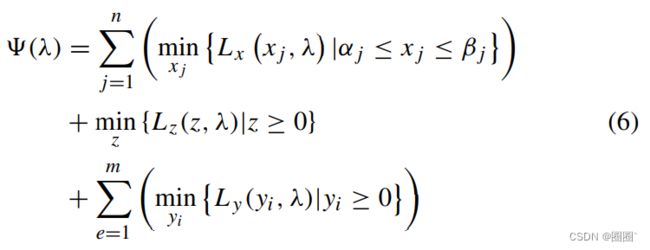
作为这些计算的一个自然部分,我们得到了xj (λ), yi(λ) 和 z(λ)的显式表达式。将这些重新插入(6)后,对偶问题可以表述为以下最大化问题
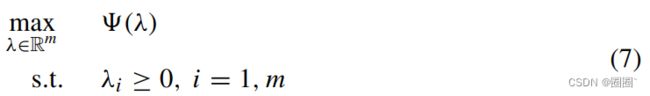 由于对偶函数是凹的,(7)中的最大化问题是凸的(Andreasson et al. 2005)。当得到对偶问题的解时,可以通过将最优 λ∗ 重新插入xj (λ)、yi(λ) 和 z(λ) 的表达式来计算最优原始解。如前所述,存在几种解决策略来解决(7)所述类型的优化问题。这里选择了原始/对偶方法,这意味着必须形成另一个拉格朗日方法,即。
由于对偶函数是凹的,(7)中的最大化问题是凸的(Andreasson et al. 2005)。当得到对偶问题的解时,可以通过将最优 λ∗ 重新插入xj (λ)、yi(λ) 和 z(λ) 的表达式来计算最优原始解。如前所述,存在几种解决策略来解决(7)所述类型的优化问题。这里选择了原始/对偶方法,这意味着必须形成另一个拉格朗日方法,即。

η ∈ R m \eta \in \mathbb R^m η∈Rm 是一个拉格朗日乘子向量,要求满足i = 1, m时 η i ≥ 0 η_i≥0 ηi≥0 和 λ i ≥ 0 λ_i≥0 λi≥0 的条件。请注意,原始/对偶类型求解器现在将 λ λ λ 称为原始变量,将 η η η 称为对偶变量,而不是MMA子问题的原始和对偶变量。一阶最优性条件,即Karush-Kuhn-Tucker (KKT)条件(Luenberger and Ye 2008;Andreasson et al. 2005),可以表述为

然后采用内点法求解上述方程组。求解过程包括在每个互补松弛条件的右侧添加一个惩罚参数 μ,使条件变为 η i λ i = μ η_iλ_i = μ ηiλi=μ。对互补松弛条件的修正等价于在对偶函数上增加一个对数障碍,即 μ Σ i m = l o g ( η i ) μ \Sigma ^m_i=log(η_i) μΣim=log(ηi),并解释 η i > 0 η_i >0 ηi>0作为松弛变量(Andreasson et al. 2005)。修正后的KKT方程组可以用牛顿法求解。由此产生的线性系统大小为2m × 2m,但可以重写为m × m系统的形式
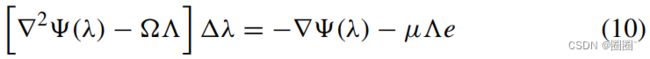 其中 Λ \Lambda Λ 和 Ω \Omega Ω 是对角线上分别为 1 λ i \frac{1}{λ_i} λi1 和 η i η_i ηi 的对角线矩阵,e是1的向量。η的搜索方向如下所示
其中 Λ \Lambda Λ 和 Ω \Omega Ω 是对角线上分别为 1 λ i \frac{1}{λ_i} λi1 和 η i η_i ηi 的对角线矩阵,e是1的向量。η的搜索方向如下所示
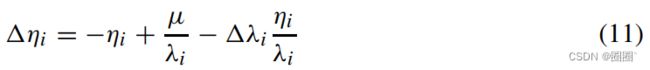
基于计算得到的搜索方向,执行直线搜索,使所有 η ′ s η's η′s 和 λ ′ s λ's λ′s 都严格为正。这个要求等价于找到最大 θ ≤ 1 θ≤1 θ≤1,使得

对于所有i = 1, m。当θ = 1时,这相当于一个完整的牛顿步长。将每个障碍问题求解到一个使KKT残差的无穷范数小于0.9μ的容限,即 ∣ ∣ K K T ∣ ∣ ∞ < 0.9 μ ||KKT||_\infty < 0.9μ ∣∣KKT∣∣∞<0.9μ,之后μ减小为原来的10倍。该过程一直持续到 μ < 1 0 − 7 μ < 10^{−7} μ<10−7。
最后,为了确保实现的鲁棒性,通过向Hessian中添加一个缩放的单位矩阵来更新(10)中的Hessian,即γI。参数γ可以通过应用Levenberg-Marquardt算法(Andreasson et al. 2005)或启发式更新来确定。在提出的实现中,使用了启发式更新,使γ被选择为10−5 tr(Hessian)或10−7的最大值。除了Hessian的启发式更新之外,还要求搜索方向实际上是上升方向。当搜索方向与(8)的梯度之间的内积大于零时,就满足这个条件。这些检查应该确保Hessian的正定性,并且搜索方向始终是上升方向。
论文:Parallel framework for topology optimization
using the method of moving asymptotes.