点云序列时序特征提取方法整理

对于连续的点云序列，点云在空间上是无序的，但在时间上是有序的。由于空间上的无序性，传统卷积无法直接应用于原始点云，因此时序点云特征提取方法可以分为

1. 基于体素分割的方法
2. 基于原始点云的方法

基于体素的方法通常是将每一帧的点云划分为多个有序区域，在每个区域内部提取特征后经过pooling操作将无序点云转换为有序点云，之后就可以使用传统卷积的方法进一步进行特征编码。

基于原始点云的方法通常首先进行点云的下采样，之后对每个采样点提取局部特征。
本文对一些论文中点云时空特征提取方法做出一些总结。

1. 基于原始点云的方法

1.1 PSTNET

标题：PSTNET: POINT SPATIO-TEMPORAL CONVOLUTION ON POINT CLOUD SEQUENCES

作者：Hehe Fan, Xin Yu, Yuhang Ding, Yi Yang & Mohan Kankanhalli

代码：https://github.com/hehefan/Point-Spatio-Temporal-Convolution

仿照传统3D卷积的概念提出了适用于连续点云的时空4D卷积。在空间上为通过相对坐标产生卷积核。输入tensor： $C\times L\times N$，输出tensor：$C^{\prime }\times L^{\prime }\times N^{\prime }$，其中 $L$ 为序列长度，$N$ 为每帧点点云中点的数量。

对于t时刻的点 $(x,y)$，可以通过3D卷积来提取时空局部特征，过程可以用下式描述
$$F_t^{{}^{\prime }(x,y)}=\sum _{k=-\lfloor l/2\rfloor }^{\lfloor l/2\rfloor }\sum _{i=-\lfloor h/2\rfloor }^{\lfloor h/2\rfloor }\sum _{j=-\lfloor w/2\rfloor }^{\lfloor w/2\rfloor }{W}_k^{(i,j)}\cdot F_{t+k}^{(x+i,y+j)}$$
传统3D卷积：输入tensor：$C\times L\times H\times W$，输出tensor：$C^{\prime }\times L^{\prime }\times H^{\prime }\times W^{\prime }$。
PSTNET的方法：

图1

如上图，有5帧连续点云。首先根据时间滑动步长 $s_t=2$，选择出第1，2，3帧点云作为采样帧。其次在每个采样帧中采样 $N^{\prime }=2$ 个点（anchor points）。根据时间卷积核的大小 $l$，将每个采样点转换到前后相邻帧中。为每个采样点在本帧以及前后相邻帧中以 $r$ 为半径搜索邻域点，构造出“point tube”。之后通过空间卷积提取每个采样点的空间局部特征 ${\mathbb{R}}^{L^{\prime }\times l\times N^{\prime }\times C_m}$。之后时间卷积将每个滑动串口内的 $l$ 帧的空间特征编码成时间特征 ${\mathbb{R}}^{L^{\prime }\times N^{\prime }\times C^{\prime }}$。

参数：

• $l=3$：时间卷积核大小
• $s_t=2$：时间卷积滑动步长
• $r$：空间邻域半径

时空点云卷积：

由于点云在空间上是无序而不规则的，且空间和时间维度是正交的。因此可以将时间和空间解耦，先在空间上卷积，再在时间上卷积。

空间卷积
$$F_t^{{}^{\prime }(x,y,z)}=\sum _{k=-\lfloor l/2\rfloor }^{\lfloor l/2\rfloor }{T}_k\cdot \sum _{||({\delta }_x,{\delta }_y,{\delta }_z)||\le r}{S}^{({\delta }_x,{\delta }_y,{\delta }_z)}\cdot F_{t+k}^{(x+{\delta }_x,y+{\delta }_y,z+{\delta }_z)}$$
空间上的不规则性导致我们无法直接定义空间卷积核，因此PSTNET通过相对坐标来产生卷积核。
$$\sum _{||({\delta }_x,{\delta }_y,{\delta }_z)||\le r}{S}^{({\delta }_x,{\delta }_y,{\delta }_z)}\cdot F_t^{(x+{\delta }_x,y+{\delta }_y,z+{\delta }_z)}=\sum _{||({\delta }_x,{\delta }_y,{\delta }_z)||\le r}f(({\delta }_x,{\delta }_y,{\delta }_z);\theta )\cdot F_t^{(x+{\delta }_x,y+{\delta }_y,z+{\delta }_z)}$$

$$f(({\delta }_x,{\delta }_y,{\delta }_z);\theta )={\theta }_d\cdot ({\delta }_x,{\delta }_y,{\delta }_z{)}^T\cdot 1\odot {\theta }_s$$

其中 ${\theta }_d\in {\mathbb{R}}^{C_m\times 3}$，${\theta }_s\in {\mathbb{R}}^{C_m\times C}$，$1=(1,...,1)\in {\mathbb{R}}^{1\times C}$

$f$ 为每一个相对坐标都产生一个不同的空间卷积核。

时间卷积

$T\in {\mathbb{R}}^{C^{\prime }\times C_m\times l}$

缺点：除非增大邻域搜索半径，否则无法通过堆叠更多的层获得空间上更大的感受野。

1.2 PointRNN

标题：PointRNN: Point Recurrent Neural Network for Moving Point Cloud Processing

作者：Hehe Fan, Yi Yang

代码：https://github.com/hehefan/PointRNN

传统的RNN通过将此时刻的输入和上一时刻的状态concat在一起来融合之前时间步的信息。但是无法直接用于点云。point-rnn的目标就是根据点的坐标融合过去和现在的点云特征。即给定点云坐标及特征 $(P_t,X_t)$ 和 $(P_{t-1},S_{t-1})$。对于 $P_t$ 中的第i个点 $P_t^i$，首先找到该点在前一帧点云 $P_{t-1}$ 的k个近邻。设 $P_{t-1}^j$ 是其中一个邻居点。将第i个点的特征 $X_t^i$、邻居点上个时间的状态 $S_{t-1}^j$、邻居点到第i个点的位移向量$P_t^i-P_{t-1}^j$ concatenate在一起，通过FC层融合。之后通过在k这个维度pooling，得到一个单独的特征表示，为第t个时间步的状态 $S_t$。

$$n\times d(P_t,X_t)\to n\times k\times (d+d^{\prime }+3)\underset{FC}{\to }n\times k\times d^{\prime }\underset{pooling}{\to }n\times d^{\prime }$$

因此，PointRNN中，在第 $t$ 个时间步的状态更新由下式描述：
$$S_t=point-rnn((P_t,X_t),(P_{t-1},S_{t-1});W,b)={\left\{\underset{j|P_{t-1}^j\in \mathcal{N}(P_t^i)}{\mathrm{pooling}}\left\{W\cdot \left[X_t^i,S_{t-1^i},P_t^i-P_{t-1}^j\right]+b\right\}\right\}}_{i\in \{1,...,n\}}$$

1.3 MoNet

标题：MoNet: Motion-based Point Cloud Prediction Network

作者：Fan Lu, Guang Chen, Yinlong Liu Zhijun Li, Sanqing Qu, Tianpei Zou

代码：https://github.com/ispc-lab/MoNet

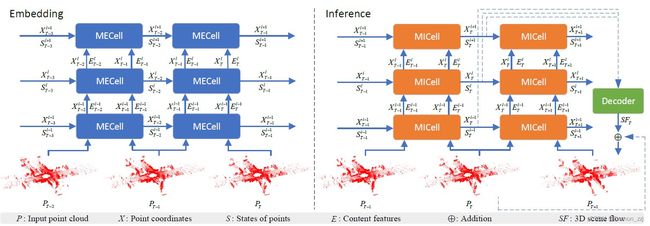
MoNet用于点云预测，主要分为两部分：Embedding和Inference。其中Embedding用于提取特征，分为 Content encoder和 Motion encoder。分别提取点云帧内容特征和点云帧间运动特征。

图2

图3

Content encoder

给定时刻t、第 $l-1$ 层的点云坐标 $X_t^{l-1}$ 和特征 $E_t^{l-1}$，首先使用 Furthest Point Sampling（FPS）从 $X_t^{l-1}$ 采样出 $N_l$ 个点 $X_t^l$。对于 $X_t^l$ 中的每一点 $x_i$，在 $X_t^{l-1}$ 中使用KNN方法找出它的k个邻居点 $\{x_i^1,x_i^2,...,x_i^k\}$，相对坐标 $\{x_i^1-x_i,x_i^2-x_i,...,x_i^k-x_i\}$以及相对距离 $\{||x_i^1-x_i||,...,||x_i^k-x_i||\}$。将以上三种特征和这k个点的内容特征 $\{e_i^1,...,e_i^k\}$ concat在一起产生一个点的空间局部融合特征。之后将所有点的空间局部融合特征输入到MLP中，pooling得到第 $l$ 层的内容特征 $E_t^l$。

Motion encoder

用于提取连续两帧点云的运动信息。输入为 $(X_t^l,E_t^l)$，$(X_{t+1}^l,E_{t+1}^l)$。对于 $X_t^l$ 中的每一点 $x_i$，在 $X_{t+1}^l$ 中使用KNN方法找出它的k个邻居点 $\{x_i^1,x_i^2,...,x_i^k\}$。使用与Content encoder相似的策略来提取两帧之间的运动特征。之后输入到MLP中，pooling得到第 $l$ 层的运动特征 $M_t^l$。

1.4 MeteorNet

标题：MeteorNet: Deep Learning on Dynamic 3D Point Cloud Sequences

作者：Xingyu Liu, Mengyuan Yan, Jeannette Bohg

代码：https://github.com/xingyul/meteornet

文章中关键模块是Meteor Module，输入是序列点云 $S=(S_1,S_2,...,S_T)$，输出是S中每个点 $p_i^{(t)}$的特征向量 $h(p_i^{(t)})$。第一步是找到点 $p_i^{(t)}$ 在第t帧和附近帧的邻居点来构成一个时空局部区域 $\mathcal{N}(p_i^{(t)})$。假设 $p_j^{(t^{\prime })}$是其中一个邻居，点 $p_i^{(t)}$ 的时空局部特征论文中有两个版本：

• 当帧之间对应关系比较重要时，将两个点的特征、两个点时空位置的差异concat之后输入进MLP $\zeta$。

$$h(p_i^{(t)})=\underset{p_j^{(t^{\prime })}\in \mathcal{N}(p_i^{(t)})}{\mathrm{MAX}}\{\zeta (f_j^{(t^{\prime })},f_i^{(t)},X_j^{(t^{\prime })}-X_i^{(t)},t^{\prime }-t)\}$$

• 当帧之间对应关系不重要时（如语义分割），将点 $p_j^{(t^{\prime })}$ 的特征、两个点时空位置的差异concat之后输入进MLP $\zeta$。
  $$h(p_i^{(t)})=\underset{p_j^{(t^{\prime })}\in \mathcal{N}(p_i^{(t)})}{\mathrm{MAX}}\{\zeta (f_j^{(t^{\prime })},X_j^{(t^{\prime })}-X_i^{(t)},t^{\prime }-t)\}$$

对于局部区域 $\mathcal{N}$ 也有两种构建方式：

图4

• Direct grouping

  直接使用半径 $r$ 来构建邻域，半径 $r$ 随帧的差异 $|t-t^{\prime }|$ 增大而增大。

• Chained-flow grouping

  通过scene flow的方法估计出第t帧的点 $p_i^{(t)}$ 在第t-1, t-2, … 帧的位置 $X_i^{{}^{\prime }(t-1)},X_i^{{}^{\prime }(t-2)},...$，分别以每帧的估计位置为中心以半径 $r$ 构建邻域。

1.5 Point Spatial-Temporal Transformer($PS{T}^2$)

标题：Spatial-Temporal Transformer for 3D Point Cloud Sequences

作者：Yimin Wei, Hao Liu, Tingting Xie, Qiuhong Ke, Yulan Guo

代码：无

$PS{T}^2$ 主要包含了两个模块：

• Spatio-Temporal Self-Attention(STAT)
• Resolution Embedding(RE)

图5

$PS{T}^2$ 采用了encoder-decoder的结构。encoder包含了一个backbone、一个RE模块和一个STSA模块。decoder包含了多个Feature Propagation（PointNet++）层。

输入为点云序列 $[S_1,S_2,...,S_T]$，首先使用FPS在 $S_1$ 中采样m个种子点。在 $[S_1,S_2,...,S_T]$上用一定半径 $r$ 搜索这m个种子点的邻居点。之后使用两个 Set Abstraction（PointNet++）层来提取局部特征 $h_i^{(t)}\in {\mathbb{R}}^{s\times d}$。

Resolution Embedding(RE)

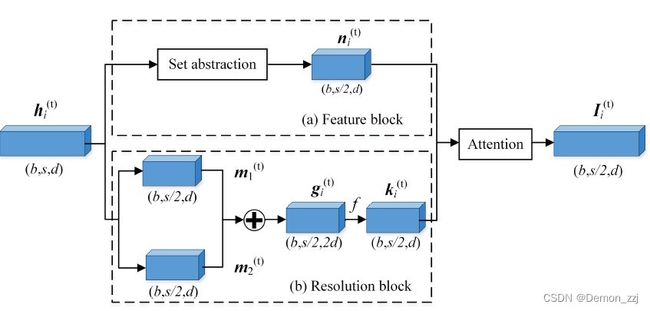
RE模块用于提高每帧中点的分辨率，主要包含一个feature block和一个resolution block。feature block用于进一步提取语义特征，resolution block用于进一步提取空间邻域信息。

图5

• Feature block

  对 $h_i^{(t)}$ 再用一个Set Abstraction 层得到 $n_i^{(t)}\in {\mathbb{R}}^{s/2\times d}$。

• Resolution block

  将 $h_i^{(t)}$ 在空间维度上分为 $m_1^{(t)}$ 和 $m_2^{(t)}$，再将它们再特征维度上concat得到 $g_i^{(t)}\in {\mathbb{R}}^{s/2\times 2d}$。之后通过MLP进一步提取特征 $k_i^{(t)}\in {\mathbb{R}}^{s/2\times d}$

Feature block 和 Resolution block 的结果通过MLP和softmax产生注意力权重 $a_1,a_2$，最终特征为二者加权和 $I_i^{(t)}\in {\mathbb{R}}^{s/2\times d}$。
$$I_i^{(t)}=a_1\cdot k_i^{(t)}+a_2\cdot n_i^{(t)}$$

Spatio-Temporal Self-Attention(STSA)

STSA模块用于融合帧间特征并且捕获时空邻域信息。将第i帧的空间特征 $I_i^{(t)}$ 分成若干个patch后输入进 Self-Attention（这一部分讲得不是很清楚）。

未完待续。。。