- 蒙特卡罗方法的原理
蒙特卡罗法是一种通过采样对问题进行近似求解的方法。通过采样若干经历完整的状态序列来估计状态的真实价值。在有了很多组这样经历完整的状态序列,就可以用它来近似的估计状态价值,进而求解预测问题。蒙特卡罗法求解强化学习预测,每个状态的价值函数只需要求出所有的完整序列中该状态出现时候的收获再取平均值即可近似求解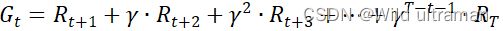 ,对于蒙特卡罗法的首次访问(first visit) 和每次访问(every visit) 用 ,对于蒙特卡罗法的首次访问(first visit) 和每次访问(every visit) 用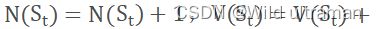 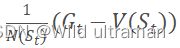 ,episodes是多轮采样的数据,每一轮包含了每一个采样到的状态,动作、奖励和它的下一个状态,用元组(s, a, r, s_next) 表示。输入:状态集S, 动作集A, 即时奖励R,衰减因子γ, 探索率ϵ。输出:最优的动作价值函数q*和最优策略π*。首先初始化所有的动作价值Q(S,a)=0,状态次数N(S,a)=0,采样次数k=0,随机初始化一个策略π。其次k=k+1, 于策略π进行第k次蒙特卡罗采样,得到一个完整的状态序列: ,episodes是多轮采样的数据,每一轮包含了每一个采样到的状态,动作、奖励和它的下一个状态,用元组(s, a, r, s_next) 表示。输入:状态集S, 动作集A, 即时奖励R,衰减因子γ, 探索率ϵ。输出:最优的动作价值函数q*和最优策略π*。首先初始化所有的动作价值Q(S,a)=0,状态次数N(S,a)=0,采样次数k=0,随机初始化一个策略π。其次k=k+1, 于策略π进行第k次蒙特卡罗采样,得到一个完整的状态序列: 。对于该状态序列里出现的每一状态行为对, 计算其收获,更新其计数N(s,a)和行为价值函数Q(s,a)。 。对于该状态序列里出现的每一状态行为对, 计算其收获,更新其计数N(s,a)和行为价值函数Q(s,a)。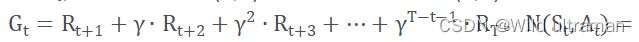  基于新计算出的动作价值,更新当前的ϵ−贪婪策略,k为采样轮数。 基于新计算出的动作价值,更新当前的ϵ−贪婪策略,k为采样轮数。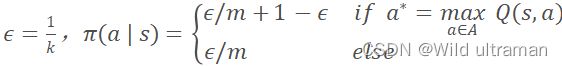 如果所有的Q(s,a)收敛,则对应的所有Q(s,a)即为最优的动作价值函数.对应的策略即为最优策略。否则重新基于策略π进行第k次蒙特卡罗采样,得到一个完整的状态序列。 如果所有的Q(s,a)收敛,则对应的所有Q(s,a)即为最优的动作价值函数.对应的策略即为最优策略。否则重新基于策略π进行第k次蒙特卡罗采样,得到一个完整的状态序列。 2.解释代码中,动作价值函数计算时,为什么没有直接应用多个完整经历的平均值。 在蒙特卡洛算法评估策略的时候要针对多个包含同一状态的完整状态序列求收获继而求收获的平均值.在状态转移过程中,某一需要计算的状态可能出现在序列的多个位置,也就是说个体在与环境交互的过程中从某状态出发后又一次或多次返回该状态.根据收获的定义,不同时刻的同一状态其计算得到的收获值是不一样的。我们有两种方法可以选择,一是仅把状态序列中第一次出现该状态时收获值纳入到收获平均值的计算中;另一种是针对一个状态序列中每次出现的该状态,都计算对应的收获值并纳入收获平均值的计算当中.两种方法对应的蒙特卡洛评估分别称为首次访问和每次访问蒙特卡洛评估。因此,在求解状态收获的平均值的过程中,我们使用一种非常实用的,不需要存储所有历史收获的计算方法:累进更新平均值。累进更新平均值利用前一次的平均值和当前数据以及数据总个数来计算新的平均值:当每产生一个需要平均的新数据xk时,先计算xk与先前平均值μk−1的差,再将这个差值乘以一定的系数1k后作为误差对旧平均值进行修正。 3.从实现来看,蒙特卡罗方法的优点和缺点是什么?如果针对缺点进行改进,你有什么想法? 优点:蒙特卡罗学习能在不清楚MDP状态转移概率及即时奖励的情况下,直接从经历完整的Episode来学习状态价值,通常情况下某状态的价值等于在多个Episode中以该状态算得到的所有收获的平均。该算法通过考虑采样轨迹,克服了模型未知给策略估计造成的困难。 缺点:此算法需在完成一个采样轨迹后再更新策略的值估计,而基于动态规划的策略迭代和值迭代算法在每执行一步策略后就进行值函数更新。两者相比,蒙特卡洛算法的效率要低得多。 想法:蒙特卡罗学习是指在不清楚MDP状态转移概率及即时奖励的情况下,直接从经历完整的Episode来学习状态价值,通常情况下某状态的价值等于在多个Episode中以该状态算得到的所有收获的平均。对此,可以尝试用快速高效的方法产生高质量的随机数,通过建立零驱动估计,单驱动估计俩种新模式对随机数生成方法进行改进是蒙特卡罗方法应用的关键并直接影响其时间复杂度。 4、代码中有环境的奖励作了更改,请更改代码中的奖励值,再运行,比较运行的效果,你可得出什么结论? import gym import numpy as np def on_policy_mc_mg(episode_num, env, gamma, first_every, eps): policy = np.ones((env.observation_space.n, env.action_space.n)) / env.action_space.n cnt = np.zeros_like(policy) q = np.zeros_like(policy) # 存储过程中的q值,用于计算最终q值 for epi in range(episode_num): # 迭代episode_num次,生成episode_num个序列 g = 0 # 即G,累积回报 state = env.reset()[0] # 重置环境 a_s = [] # 存储一个序列中的动作、状态和奖励 while True: # 采样一个完整经历,也就是一轮,记录过程中的动作、状态和奖励到a_s, action = np.random.choice(env.action_space.n, p=policy[state]) new_state, reward, done, info, _ = env.step(action) # 放到环境中执行后,得到新状 if reward == 1: reward = 200 elif reward == 0 and done: # 到达终点 reward = -200 elif reward == 0 and state == new_state: reward = -200 done = True else: reward = -10 if first_every == 'every': # 是every visit 还是first vist a_s.append((action, state, reward)) else: if (action, state, reward) not in a_s: a_s.append((action, state, reward)) state = new_state if done: break g = 0 for a, s, r in reversed(a_s): g = r + gamma * g cnt[s][a] += 1 q[s][a] += (g - q[s][a]) / cnt[s][a] ac = np.argmax(q[s]) # 找到q值最大的对应的动作 policy[s] = eps / env.action_space.n policy[s][ac] = 1 - eps + eps / env.action_space.n if (epi + 1) % 1000 == 0: print(f'epi: {epi}, g = {g}') # eps = 1.0 / (epi + 2) return policy, q if __name__ == '__main__': env = gym.make("FrozenLake-v1", map_name="4x4", is_slippery=False) # gamma = 0.7 eps = 0.1 # 改掉的,用eps-软策略 episode_num = 10000 # 5000 first_every = 'first' p, q = on_policy_mc_mg(episode_num, env, gamma, first_every, eps) env = gym.make("FrozenLake-v1", map_name="4x4", is_slippery=False, render_mode="human") state = env.reset()[0] g = i = 0 import time while True: i += 1 action = p[state].argmax() # 测试时直接以策略的最大值处理 state, reward, done, _, _ = env.step(action) env.render() time.sleep(1) g = reward if done: break env.close() 运行结果: epi: 999, g = 5.882999999999997 epi: 1999, g = 5.882999999999997 epi: 2999, g = 5.882999999999997 epi: 3999, g = 5.882999999999997 epi: 4999, g = 5.882999999999997 epi: 5999, g = -14.11733 epi: 6999, g = 5.882999999999997 epi: 7999, g = 5.882999999999997 epi: 8999, g = -19.882131 epi: 9999, g = 5.882999999999997  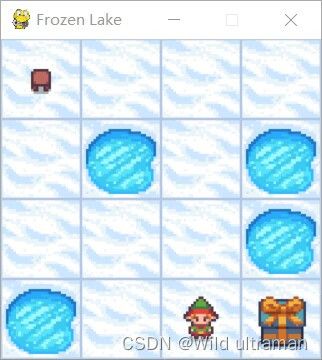 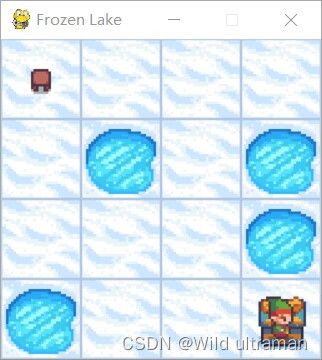
结论:通过改变训练传入参数的 gamma值 ,使其略微降低改为0.7 后发现得到奖励值g 随gamma的减小而减小。通过改变环境奖励的设定发现对环境奖励设定的好坏,也是影响训练的重要因素。 |