逻辑回归 预测癌症数据
目录
一:加载数据
二:数据集划分
三:选择算法
四:网格模型 超参调优
五:模型预测
六:模型保存和使用
七:完整源码分享
八:预测与实际比对
一:加载数据
from sklearn.datasets import load_breast_cancer
# 加载肺癌数据
cancer_data = load_breast_cancer()
X = cancer_data.data
Y = cancer_data.target
print(X, X.shape)提取特征数据,结果如下
[[1.799e+01 1.038e+01 1.228e+02 ... 2.654e-01 4.601e-01 1.189e-01]
[2.057e+01 1.777e+01 1.329e+02 ... 1.860e-01 2.750e-01 8.902e-02]
[1.969e+01 2.125e+01 1.300e+02 ... 2.430e-01 3.613e-01 8.758e-02]
...
[1.660e+01 2.808e+01 1.083e+02 ... 1.418e-01 2.218e-01 7.820e-02]
[2.060e+01 2.933e+01 1.401e+02 ... 2.650e-01 4.087e-01 1.240e-01]
[7.760e+00 2.454e+01 4.792e+01 ... 0.000e+00 2.871e-01 7.039e-02]] (569, 30)print(Y, Y.shape)提取标签数据,结果如下,共2种结果为0和1
[0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 1 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
1 0 0 0 0 0 0 0 0 1 0 1 1 1 1 1 0 0 1 0 0 1 1 1 1 0 1 0 0 1 1 1 1 0 1 0 0
1 0 1 0 0 1 1 1 0 0 1 0 0 0 1 1 1 0 1 1 0 0 1 1 1 0 0 1 1 1 1 0 1 1 0 1 1
1 1 1 1 1 1 0 0 0 1 0 0 1 1 1 0 0 1 0 1 0 0 1 0 0 1 1 0 1 1 0 1 1 1 1 0 1
1 1 1 1 1 1 1 1 0 1 1 1 1 0 0 1 0 1 1 0 0 1 1 0 0 1 1 1 1 0 1 1 0 0 0 1 0
1 0 1 1 1 0 1 1 0 0 1 0 0 0 0 1 0 0 0 1 0 1 0 1 1 0 1 0 0 0 0 1 1 0 0 1 1
1 0 1 1 1 1 1 0 0 1 1 0 1 1 0 0 1 0 1 1 1 1 0 1 1 1 1 1 0 1 0 0 0 0 0 0 0
0 0 0 0 0 0 0 1 1 1 1 1 1 0 1 0 1 1 0 1 1 0 1 0 0 1 1 1 1 1 1 1 1 1 1 1 1
1 0 1 1 0 1 0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 0 1 1 1 0 1 0 1 1 1 1 0 0 0 1 1
1 1 0 1 0 1 0 1 1 1 0 1 1 1 1 1 1 1 0 0 0 1 1 1 1 1 1 1 1 1 1 1 0 0 1 0 0
0 1 0 0 1 1 1 1 1 0 1 1 1 1 1 0 1 1 1 0 1 1 0 0 1 1 1 1 1 1 0 1 1 1 1 1 1
1 0 1 1 1 1 1 0 1 1 0 1 1 1 1 1 1 1 1 1 1 1 1 0 1 0 0 1 0 1 1 1 1 1 0 1 1
0 1 0 1 1 0 1 0 1 1 1 1 1 1 1 1 0 0 1 1 1 1 1 1 0 1 1 1 1 1 1 1 1 1 1 0 1
1 1 1 1 1 1 0 1 0 1 1 0 1 1 1 1 1 0 0 1 0 1 0 1 1 1 1 1 0 1 1 0 1 0 1 0 0
1 1 1 0 1 1 1 1 1 1 1 1 1 1 1 0 1 0 0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 0 0 0 0 0 0 1] (569,)二:数据集划分
# 数据划分
X_train, X_test, y_train, y_test = train_test_split(X, Y, test_size=0.3, random_state=666)数据集划分为训练集和测试集,比例设置 、随机划分数设置
三:选择算法
# 选择一个算法
# multi_class:多分类参数是在 二分类基础上进行
# OVR:一对多 把多元的转为二分类 有几个点就分几次处理 4特征
# OVO:一对一 把多元的转为更多的二分类,求概率,然后进行比较,求出最大的概率(耗时较多)
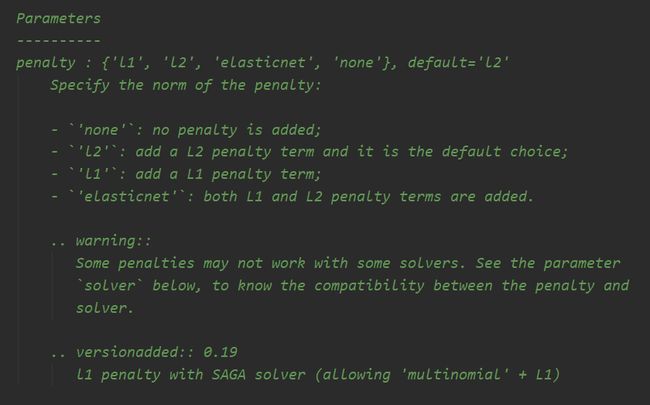
# penalty="l2":损失函数 penalty : {'l1', 'l2', 'elasticnet', 'none'}, default='l2'
# class_weight:权重 class_weight : dict or 'balanced', default=None
# solver: {'newton-cg', 'lbfgs', 'liblinear', 'sag', 'saga'}, \
# default='lbfgs'
model = LogisticRegression()
param_list = [
{
'penalty': ['l1', 'l2'],
'class_weight': [None, 'balanced'],
'solver': ['newton-cg', 'lbfgs', 'liblinear'],
'multi_class': ['ovr']
},
{
'penalty': ['l1', 'l2'],
'class_weight': [None, 'balanced'],
'solver': ['newton-cg', 'lbfgs', 'sag'],
'multi_class': ['multinomial']
}
]penalty="l2":正则化防止过拟合
solver:优化算法选择参数(在下一步中使用网格模型 得出超参数的最优解)
逻辑回归算法LogisticRegression,重要参数如下
multi_class:多分类参数是在 二分类基础上进行
OVR:一对多 把多元的转为二分类 有几个点就分几次处理 4特征
OVO:一对一 把多元的转为更多的二分类,求概率,然后进行比较,求出最大的概率(耗时较多)
penalty="l2":损失函数 penalty : {'l1', 'l2', 'elasticnet', 'none'}, default='l2'
class_weight:权重 class_weight : dict or 'balanced', default=None
solver: {'newton-cg', 'lbfgs', 'liblinear', 'sag', 'saga'}, \
default='lbfgs'
四:网格模型 超参调优
# 网格算法
grid = GridSearchCV(model, param_grid=param_list, cv=10)
grid.fit(X_train, y_train)
print(grid.best_estimator_)
print(grid.best_params_)
print(grid.best_score_)
获取超参最优解,如下,模型评分值较高
LogisticRegression(multi_class='multinomial', solver='newton-cg')
{'class_weight': None, 'multi_class': 'multinomial', 'penalty': 'l2', 'solver': 'newton-cg'}
0.9547435897435899五:模型预测
# 预测模型
best_model = LogisticRegression(multi_class='multinomial', solver='newton-cg')
best_model.fit(X_train, y_train)
y_predict = best_model.predict(X_test)
print(y_predict == y_test)如下,可以看出,预测结果大致效果还是不错的
[ True True True True True True True True True True True True
True False True True True True True True True True True True
True True True True True True True True True True True True
True True True True True True True True True True True True
True True False True True True True True False True True True
True True False True True True True True True True True True
True True False True True False True True True True True True
True True True True True True True True True True True True
True True True True True True True True True True True True
True True True True True True True True True True True True
True True True False True True True True True True True True
True True True True True True True True True True False True
True True True True True True True True True True True True
True True True True True True True True True True True True
True True True]六:模型保存和使用
# 模型保存
joblib.dump(value=best_model, filename='logisticCancer.model')
# 模型使用
cancerModel = joblib.load('logisticCancer.model')七:完整源码分享
from sklearn.datasets import load_breast_cancer
from sklearn.model_selection import train_test_split, GridSearchCV
from sklearn.linear_model import LogisticRegression # 逻辑回归算法
import joblib
# 加载肺癌数据
cancer_data = load_breast_cancer()
X = cancer_data.data
Y = cancer_data.target
# print(X, X.shape)
# print(Y, Y.shape)
# 数据划分
X_train, X_test, y_train, y_test = train_test_split(X, Y, test_size=0.3, random_state=666)
# 选择一个算法
# multi_class:多分类参数是在 二分类基础上进行
# OVR:一对多 把多元的转为二分类 有几个点就分几次处理 4特征
# OVO:一对一 把多元的转为更多的二分类,求概率,然后进行比较,求出最大的概率(耗时较多)
# penalty="l2":损失函数 penalty : {'l1', 'l2', 'elasticnet', 'none'}, default='l2'
# class_weight:权重 class_weight : dict or 'balanced', default=None
# solver: {'newton-cg', 'lbfgs', 'liblinear', 'sag', 'saga'}, \
# default='lbfgs'
model = LogisticRegression()
param_list = [
{
'penalty': ['l1', 'l2'],
'class_weight': [None, 'balanced'],
'solver': ['newton-cg', 'lbfgs', 'liblinear'],
'multi_class': ['ovr']
},
{
'penalty': ['l1', 'l2'],
'class_weight': [None, 'balanced'],
'solver': ['newton-cg', 'lbfgs', 'sag'],
'multi_class': ['multinomial']
}
]
# 网格算法
# grid = GridSearchCV(model, param_grid=param_list, cv=10)
# grid.fit(X_train, y_train)
# print(grid.best_estimator_)
# print(grid.best_params_)
# print(grid.best_score_)
# 预测模型
best_model = LogisticRegression(multi_class='multinomial', solver='newton-cg')
best_model.fit(X_train, y_train)
y_predict = best_model.predict(X_test)
print(y_predict == y_test)
模型预测,结果分析如下,准确率相对来说还是比较高的
八:预测与实际比对
import pandas as pd线性图 回归模型
import matplotlib.pyplot as plt
test_pre = pd.DataFrame({"test": y_test.tolist(),
"pre": y_predict.flatten()
})
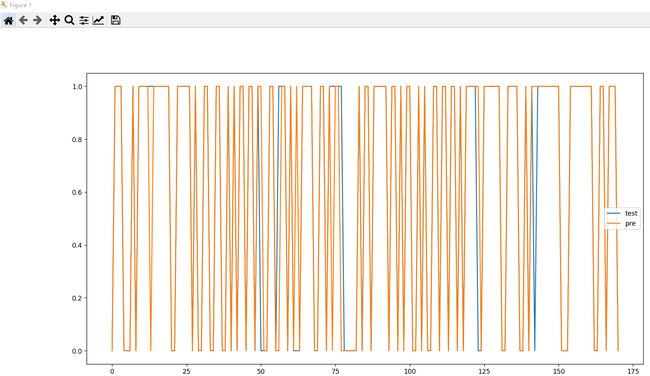
test_pre.plot(figsize=(18, 10))
plt.show()点状图 回归模型
import matplotlib.pyplot as plt
# 预测与实际
plt.scatter(y_test, y_predict, label="test")
plt.plot([y_test.min(), y_test.max()],
[y_test.min(), y_test.max()],
'k--',
lw=3,
label="predict"
)
plt.show()有上面两图,分析得出,预测与实际的比对效果还是相当不错的