逻辑回归 鸢尾花分类预测

目录

一：加载数据

二：数据集划分

三：选择算法

四：网格模型 超参数最优解

五：鸢尾花分类预测

六：预测与实际比对

七：完整源码分享

---

一：加载数据

from sklearn.datasets import load_iris  # 鸢尾花
from sklearn.model_selection import train_test_split, GridSearchCV
from sklearn.linear_model import LogisticRegression  # 逻辑回归算法
import pandas as pd
import joblib

# 加载鸢尾花数据集
iris_data = load_iris()
X = iris_data.data
Y = iris_data.target
print(X, X.shape)

提取特征数据，结果如下

[[5.1 3.5 1.4 0.2]
 [4.9 3.  1.4 0.2]
 [4.7 3.2 1.3 0.2]
 [4.6 3.1 1.5 0.2]
 [5.  3.6 1.4 0.2]
 [5.4 3.9 1.7 0.4]
 [4.6 3.4 1.4 0.3]
 [5.  3.4 1.5 0.2]
 [4.4 2.9 1.4 0.2]
 [4.9 3.1 1.5 0.1]
 [5.4 3.7 1.5 0.2]
 [4.8 3.4 1.6 0.2]
 [4.8 3.  1.4 0.1]
 [4.3 3.  1.1 0.1]
 [5.8 4.  1.2 0.2]
 [5.7 4.4 1.5 0.4]
 [5.4 3.9 1.3 0.4]
 [5.1 3.5 1.4 0.3]
 [5.7 3.8 1.7 0.3]
 [5.1 3.8 1.5 0.3]
 [5.4 3.4 1.7 0.2]
 [5.1 3.7 1.5 0.4]
 [4.6 3.6 1.  0.2]
 [5.1 3.3 1.7 0.5]
 [4.8 3.4 1.9 0.2]
 [5.  3.  1.6 0.2]
 [5.  3.4 1.6 0.4]
 [5.2 3.5 1.5 0.2]
 [5.2 3.4 1.4 0.2]
 [4.7 3.2 1.6 0.2]
 [4.8 3.1 1.6 0.2]
 [5.4 3.4 1.5 0.4]
 [5.2 4.1 1.5 0.1]
 [5.5 4.2 1.4 0.2]
 [4.9 3.1 1.5 0.2]
 [5.  3.2 1.2 0.2]
 [5.5 3.5 1.3 0.2]
 [4.9 3.6 1.4 0.1]
 [4.4 3.  1.3 0.2]
 [5.1 3.4 1.5 0.2]
 [5.  3.5 1.3 0.3]
 [4.5 2.3 1.3 0.3]
 [4.4 3.2 1.3 0.2]
 [5.  3.5 1.6 0.6]
 [5.1 3.8 1.9 0.4]
 [4.8 3.  1.4 0.3]
 [5.1 3.8 1.6 0.2]
 [4.6 3.2 1.4 0.2]
 [5.3 3.7 1.5 0.2]
 [5.  3.3 1.4 0.2]
 [7.  3.2 4.7 1.4]
 [6.4 3.2 4.5 1.5]
 [6.9 3.1 4.9 1.5]
 [5.5 2.3 4.  1.3]
 [6.5 2.8 4.6 1.5]
 [5.7 2.8 4.5 1.3]
 [6.3 3.3 4.7 1.6]
 [4.9 2.4 3.3 1. ]
 [6.6 2.9 4.6 1.3]
 [5.2 2.7 3.9 1.4]
 [5.  2.  3.5 1. ]
 [5.9 3.  4.2 1.5]
 [6.  2.2 4.  1. ]
 [6.1 2.9 4.7 1.4]
 [5.6 2.9 3.6 1.3]
 [6.7 3.1 4.4 1.4]
 [5.6 3.  4.5 1.5]
 [5.8 2.7 4.1 1. ]
 [6.2 2.2 4.5 1.5]
 [5.6 2.5 3.9 1.1]
 [5.9 3.2 4.8 1.8]
 [6.1 2.8 4.  1.3]
 [6.3 2.5 4.9 1.5]
 [6.1 2.8 4.7 1.2]
 [6.4 2.9 4.3 1.3]
 [6.6 3.  4.4 1.4]
 [6.8 2.8 4.8 1.4]
 [6.7 3.  5.  1.7]
 [6.  2.9 4.5 1.5]
 [5.7 2.6 3.5 1. ]
 [5.5 2.4 3.8 1.1]
 [5.5 2.4 3.7 1. ]
 [5.8 2.7 3.9 1.2]
 [6.  2.7 5.1 1.6]
 [5.4 3.  4.5 1.5]
 [6.  3.4 4.5 1.6]
 [6.7 3.1 4.7 1.5]
 [6.3 2.3 4.4 1.3]
 [5.6 3.  4.1 1.3]
 [5.5 2.5 4.  1.3]
 [5.5 2.6 4.4 1.2]
 [6.1 3.  4.6 1.4]
 [5.8 2.6 4.  1.2]
 [5.  2.3 3.3 1. ]
 [5.6 2.7 4.2 1.3]
 [5.7 3.  4.2 1.2]
 [5.7 2.9 4.2 1.3]
 [6.2 2.9 4.3 1.3]
 [5.1 2.5 3.  1.1]
 [5.7 2.8 4.1 1.3]
 [6.3 3.3 6.  2.5]
 [5.8 2.7 5.1 1.9]
 [7.1 3.  5.9 2.1]
 [6.3 2.9 5.6 1.8]
 [6.5 3.  5.8 2.2]
 [7.6 3.  6.6 2.1]
 [4.9 2.5 4.5 1.7]
 [7.3 2.9 6.3 1.8]
 [6.7 2.5 5.8 1.8]
 [7.2 3.6 6.1 2.5]
 [6.5 3.2 5.1 2. ]
 [6.4 2.7 5.3 1.9]
 [6.8 3.  5.5 2.1]
 [5.7 2.5 5.  2. ]
 [5.8 2.8 5.1 2.4]
 [6.4 3.2 5.3 2.3]
 [6.5 3.  5.5 1.8]
 [7.7 3.8 6.7 2.2]
 [7.7 2.6 6.9 2.3]
 [6.  2.2 5.  1.5]
 [6.9 3.2 5.7 2.3]
 [5.6 2.8 4.9 2. ]
 [7.7 2.8 6.7 2. ]
 [6.3 2.7 4.9 1.8]
 [6.7 3.3 5.7 2.1]
 [7.2 3.2 6.  1.8]
 [6.2 2.8 4.8 1.8]
 [6.1 3.  4.9 1.8]
 [6.4 2.8 5.6 2.1]
 [7.2 3.  5.8 1.6]
 [7.4 2.8 6.1 1.9]
 [7.9 3.8 6.4 2. ]
 [6.4 2.8 5.6 2.2]
 [6.3 2.8 5.1 1.5]
 [6.1 2.6 5.6 1.4]
 [7.7 3.  6.1 2.3]
 [6.3 3.4 5.6 2.4]
 [6.4 3.1 5.5 1.8]
 [6.  3.  4.8 1.8]
 [6.9 3.1 5.4 2.1]
 [6.7 3.1 5.6 2.4]
 [6.9 3.1 5.1 2.3]
 [5.8 2.7 5.1 1.9]
 [6.8 3.2 5.9 2.3]
 [6.7 3.3 5.7 2.5]
 [6.7 3.  5.2 2.3]
 [6.3 2.5 5.  1.9]
 [6.5 3.  5.2 2. ]
 [6.2 3.4 5.4 2.3]
 [5.9 3.  5.1 1.8]] (150, 4)

print(Y, Y.shape)

 提取标签数据，结果如下 

[0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
 0 0 0 0 0 0 0 0 0 0 0 0 0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 2 2 2 2 2 2 2 2 2 2 2
 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2
 2 2] (150,)

二：数据集划分

# 数据划分
X_train, X_test, y_train, y_test = train_test_split(X, Y, test_size=0.2, random_state=6)

数据集划分为训练集和测试集，划分比例设置，随机划分设置 

三：选择算法

# 选择一个算法
# multi_class:多分类参数是在 二分类基础上进行
# OVR:一对多 把多元的转为二分类 有几个点就分几次处理 4特征
# OVO:一对一 把多元的转为更多的二分类，求概率，然后进行比较，求出最大的概率(耗时较多)
# penalty="l2":损失函数  penalty : {'l1', 'l2', 'elasticnet', 'none'}, default='l2'
# class_weight:权重      class_weight : dict or 'balanced', default=None
# solver:   {'newton-cg', 'lbfgs', 'liblinear', 'sag', 'saga'}, \
#             default='lbfgs'
model = LogisticRegression()
param_list = [
    {
        'penalty': ['l1', 'l2'],
        'class_weight': [None, 'balanced'],
        'solver': ['newton-cg', 'lbfgs', 'liblinear'],
        'multi_class': ['ovr']
    },
    {
        'penalty': ['l1', 'l2'],
        'class_weight': [None, 'balanced'],
        'solver': ['newton-cg', 'lbfgs', 'sag'],
        'multi_class': ['multinomial']
    }
]

LogisticRegression重要参数

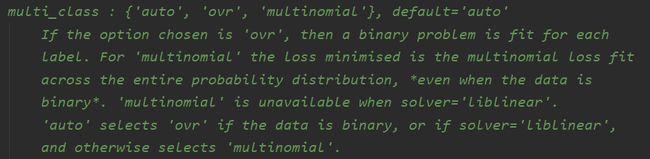
 multi_class:多分类参数是在 二分类基础上进行 auto ovr multinomial
 OVR:一对多 把多元的转为二分类 有几个点就分几次处理 4特征
 OVO:一对一 把多元的转为更多的二分类，求概率，然后进行比较，求出最大的概率(耗时较多)
 penalty="l2":正则化防止过拟合       l1  l2
 class_weight:权重      class_weight : dict or 'balanced', default=None
 solver:   {'newton-cg', 'lbfgs', 'liblinear', 'sag', 'saga'}, \
                default='lbfgs'      超参调优参数

四：网格模型 超参数最优解

# 网格算法
grid = GridSearchCV(model, param_grid=param_list, cv=10)
grid.fit(X_train, y_train)
print(grid.best_estimator_)
print(grid.best_params_)
print(grid.best_score_)

超参最优解，如下，可使用于模型预测 

LogisticRegression(multi_class='multinomial', solver='sag')
{'class_weight': None, 'multi_class': 'multinomial', 'penalty': 'l2', 'solver': 'sag'}
0.975

五：鸢尾花分类预测

# 预测模型
best_model = LogisticRegression(multi_class='multinomial', solver='sag')
best_model.fit(X_train, y_train)
y_predict = best_model.predict(X_test)
print(y_predict == y_test)

鸢尾花分类预测，结果如下，准确性较高 

[ True  True  True  True  True  True  True  True  True  True  True  True
  True  True  True  True  True  True  True  True  True  True  True  True
  True  True  True  True  True  True]

六：预测与实际比对

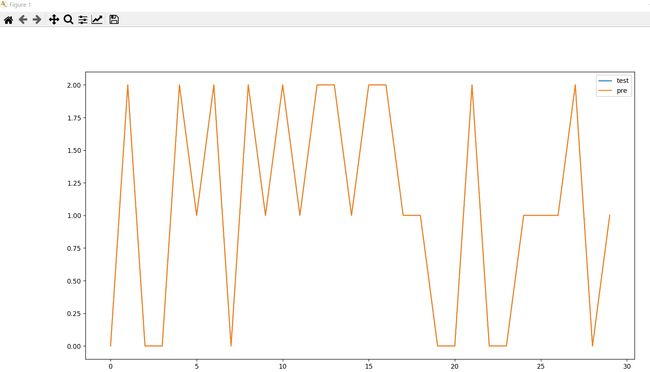
线性图 回归模型

import matplotlib.pyplot as plt

test_pre = pd.DataFrame({"test": y_test.tolist(),
                         "pre": y_predict.flatten()
                         })
test_pre.plot(figsize=(18, 10))
plt.show()

点状图 回归模型

import matplotlib.pyplot as plt

# 预测与实际
plt.scatter(y_test, y_predict, label="test")
plt.plot([y_test.min(), y_test.max()],
         [y_test.min(), y_test.max()],
         'k--',
         lw=3,
         label="predict"
         )
plt.show()

从上面两个图，得出，预测和实际比对的结果还是very good的 

七：完整源码分享

from sklearn.datasets import load_iris  # 鸢尾花
from sklearn.model_selection import train_test_split, GridSearchCV
from sklearn.linear_model import LogisticRegression  # 逻辑回归算法
import matplotlib.pyplot as plt
import pandas as pd
import joblib

# 加载鸢尾花数据集
iris_data = load_iris()
X = iris_data.data
Y = iris_data.target
# print(X, X.shape)
# print(Y, Y.shape)

# 数据划分
X_train, X_test, y_train, y_test = train_test_split(X, Y, test_size=0.2, random_state=6)

# 选择一个算法
# multi_class:多分类参数是在 二分类基础上进行
# OVR:一对多 把多元的转为二分类 有几个点就分几次处理 4特征
# OVO:一对一 把多元的转为更多的二分类，求概率，然后进行比较，求出最大的概率(耗时较多)
# penalty="l2":损失函数  penalty : {'l1', 'l2', 'elasticnet', 'none'}, default='l2'
# class_weight:权重      class_weight : dict or 'balanced', default=None
# solver:   {'newton-cg', 'lbfgs', 'liblinear', 'sag', 'saga'}, \
#             default='lbfgs'
model = LogisticRegression()
param_list = [
    {
        'penalty': ['l1', 'l2'],
        'class_weight': [None, 'balanced'],
        'solver': ['newton-cg', 'lbfgs', 'liblinear'],
        'multi_class': ['ovr']
    },
    {
        'penalty': ['l1', 'l2'],
        'class_weight': [None, 'balanced'],
        'solver': ['newton-cg', 'lbfgs', 'sag'],
        'multi_class': ['multinomial']
    }
]

# 网格算法
# grid = GridSearchCV(model, param_grid=param_list, cv=10)
# grid.fit(X_train, y_train)
# print(grid.best_estimator_)
# print(grid.best_params_)
# print(grid.best_score_)

# 预测模型
best_model = LogisticRegression(multi_class='multinomial', solver='sag')
best_model.fit(X_train, y_train)
y_predict = best_model.predict(X_test)
print(y_predict == y_test)