Python计算相关系数

最近在看地理建模题目，其中提到了建立回归模型后计算相关系数；当时有点疑问，这个相关系数是从原始数据算出，还是用回归后的拟合数据计算。
后来想了想应该是原始数据计算的，用回归方程算出的x，y肯定在一条直线上，相关系数直接就是1了。虽然想法有些耿直，但是为了验证一下，同时也顺路写写代码，于是使用Python计算相关系数。

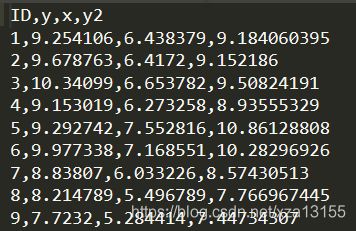
提前将数据整理为csv格式了，四列分别为ID、原始y、原始x、和拟合y。

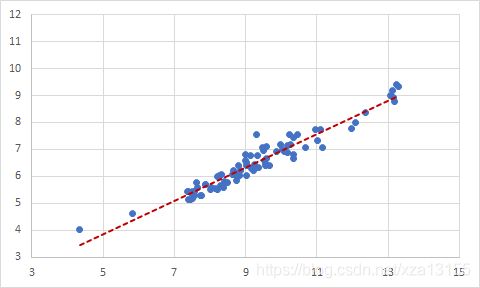
原始x和y的散点图显示x与y呈现线性相关关系。因此可以建立线性回归模型。

这是相关系数计算公式。据此计算相关关系。

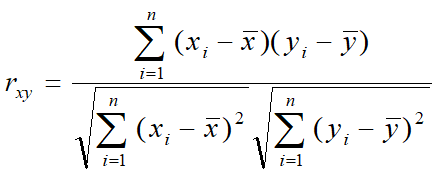
根据公式写出计算代码：

import pandas as pd
from numpy import mean
#相关系数计算公式
def R_Square(x,y):
    p1=x2=y2=0.0
    #计算平均值
    x_=mean(x)
    y_=mean(y)
    #循环读取每个值，计算对应值的累和
    for i in range(len(x)):
        p1+=(x[i]-x_)*(y[i]-y_)
        x2+=(x[i]-x_)**2
        y2+=(y[i]-y_)**2
    #print(p1,x2,y2)
    #计算相关系数
    r=p1/((x2** 0.5)*(y2** 0.5))
    return r
#读取数据
df=pd.read_csv("data.csv",encoding='utf-8')
x=df['x'].tolist()
y=df['y'].tolist()
#调用并输出相关系数
print(R_Square(x,y))

上面为拟合值与x的相关系数，下面为原始x、y的相关系数。结果与设想的一样。

新开通了本人的公众号，欢迎关注：燕南路GISer ，专注GIS干货分享，不定期更新。
主要兴趣：GIS、时空数据挖掘、python、机器学习深度学习
CSDN的部分内容会重写再搬迁到公众号，欢迎关注！