四大坐标系转换和相机标定

四大坐标系转换和相机标定

相机成像过程涉及坐标变换

包含世界坐标系(Xw,Yw,Zw)，相机坐标(Xc,Yc,Zc)，平面坐标(x,y)，像素坐标（u,v）.

一：四个不同类型的坐标系

将三维物体转换成照片上的二维坐标，由四个坐标系进行转换。

1世界坐标系

世界坐标系是一个特殊坐标系，它建立了描述其他坐标系需要的参考框架。能够用世界坐标系描述其他坐标系的位置，而不能用更大的、外部的坐标系描述世界坐标系。从非技术意义上讲，世界坐标系建立的是我们所关心的最大坐标系，而不必真的是整个世界。
用(Xw, Yw, Zw）表示。

2. 相机坐标系

以相机透镜的几何中心（光心）为原点，坐标系满足右手法则，用(Xc, Yc, Zc)来表示；相机光轴为坐标系的Z轴，X轴水平，Y轴竖直。

3. 图像物理坐标系

以CCD图像的中心为原点，坐标由 ( x , y ) (x, y)(x,y) 表示，图像坐标系的单位，一般是毫米，坐标原点为相机光轴与成像平面的交点（一般情况下，这个交点是接近于图像的正中心）。

CCD，英文全称：Charge coupled Device，中文全称：电荷耦合元件，可以称为CCD图像传感器。
CCD是一种半导体器件，能够把光学影像转化为数字信号。 CCD上植入的微小光敏物质称作像素（Pixel）。
一块CCD上包含的像素数越多，其提供的画面分辨率也就越高。

4. 图像像素坐标系

其实，当我们提及一个图像时，通常指的是图像的像素坐标系。像素坐标系的原点在左上角，并且单位为像素。

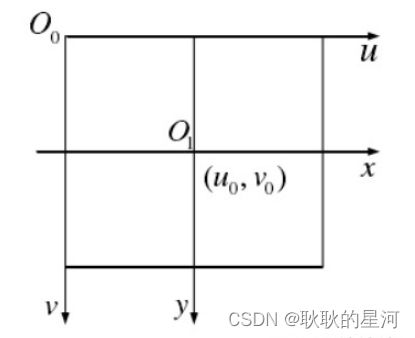
将图像坐标系的原点O1​转化到以O0 为原点的坐标系中。使用的原因：

• 如果使用图像坐标系，单位mm，其实不太好衡量具体的图像，如果按照统一的像素标准，比较容易衡量图像的质量
• 如果使用图像坐标系，然后就有四个象限，这样会有正负数的问题，但是转换成像素坐标系后，都为整数。在后续的操作和运算中，都简化很多。

二 坐标转换

1.世界坐标 → 相机坐标（刚性变换）

(Xc, Yc, Zc)代表相机坐标；(Xw, Yw, Zw）代表世界坐标；R代表正交单位旋转矩阵，t代表三维平移矢量。
根据旋转角度可以分别得三个方向上的旋转矩阵，而旋转矩阵即为他们的乘积：R=RxRyRz 顺便记录一下三个旋转矩阵的公式，经常忘记。
绕X 旋转θ 度:

绕Y 旋转θ 度:

绕Z 旋转θ 度:

如下图( 旋转θ ）：

2 相机坐标 → 图像坐标系（中心投影）

相机坐标系到图像坐标系是透视关系，利用相似三角形进行计算。

写成齐次坐标形式的矩阵相乘为：

其中f代表焦距，即相机坐标系和图像坐标系在Z轴上的差。此时投影点p的单位还是mm，并不是pixel，不方便进行后续运算。

3 图像坐标系 → 像素坐标系（离散化）

像素坐标系的原点在左上角，并且单位为像素。像素坐标系和图像坐标系都在成像平面上，只是各自的原点和度量单位不一样。图像坐标系的原点为相机光轴与成像平面的交点，通常情况下是成像平面的中点或者叫principal point。图像坐标系的单位是mm，属于物理单位，而像素坐标系的单位是pixel，我们平常描述一个像素点都是几行几列。所以这二者之间的转换如下：其中dx和dy表示每一列和每一行分别代表多少mm，即1pixel=dx mm

4、最终得到坐标系转化公式

通过上面四个坐标系的转换可以得到一个点从世界坐标系如何转到像素坐标系，如下图所示，这里有我们熟悉的内参和外参矩阵。

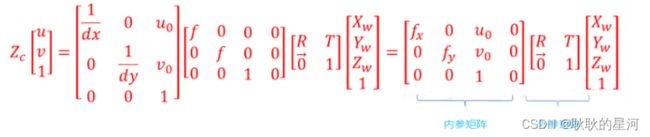
相机的内参和外参

• 外参：摄像机的旋转平移属于外参，用于描述相机在静态场景下相机的运动，或者在相机固定时，运动物体的刚性运动。因此，在图像拼接或者三维重建中，就需要使用外参来求几幅图像之间的相对运动，从而将其注册到同一个坐标系下面来.

• 内参：下面给出了内参矩阵，需要注意的是，真实的镜头还会有径向和切向畸变，而这些畸变是属于相机的内参的。由前面步骤已知像素坐标系到世界坐标系映射关系：
  所以：
  

其中，fx=f/dx,fy=f/dy,f是相机的焦距。RT是外参，矩阵K是内参，包含5个未知数，标定的时候，如果物体距离相机不同位置，那么我们必须在不同位置对相机坐标定。简单理解就是当物体离相机近的时候成像效果大，实际代表尺寸就小。因此每一个位置都要去标定。

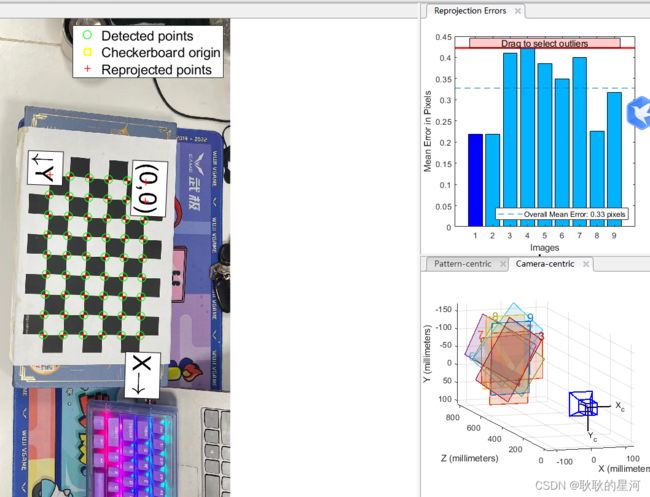
三 相机标定

实验步骤：

1.打印一张棋盘格A4纸张（黑白间距已知），并贴在一个平板上

2.针对棋盘格拍摄若干张图片（一般10-20张）

3.在图片中检测特征点（Harris特征）

4.利用解析解估算方法计算出5个内部参数，以及6个外部参数

5.根据极大似然估计策略，设计优化目标并实现参数的refinement

1 打开Matlab.界面如下图1所示。

2 点击上方“APP”功能，进入如下界面，红色部分为相机标定功能（上方为弹单目相机标定功能，下方是双目相机标定）

3 点击单目相机标定，进入如下标定界面，点击红色部分的**“下三角”**选择“From file”,选择文件夹，选择照片。

4 选择照片后，进入如下界面，选择标定板的大小（单位 mm），我的设置为25mm。

5 点击**“Calibrate”**开始标定。

6.标定参数误差。如图6中的红色部分是标定误差，标定误差平均值小于0.3个像素，相机参数可用。（从标定误差中可以看出每张照片的误差，如果某张照片误差过大，可以在左侧图片列表中将其删除，重新标定）。

7.点击图7中的红色部分进行参数保存。会出现图8的命令框，点击确定即可。

结果：
其中，“RadiaDistortion”即为相机的畸变矩阵，“IntrinsicMatrix”即为内参矩阵。