【分布外检测】《Energy-based Out-of-distribution Detection》 NIPS‘20

《Energy-based Out-of-distribution Detection》 NIPS’20

不改变模型结构，在任意模型上用能量函数替代softmax函数，识别输入数据是否为异常样本。还提出一个基于能量的正则化项，用来针对性fine-tuning模型。

解决什么问题

当模型遇到和训练数据差别很大的数据时，就会出现out-of-distribution （OOD）uncertainty，这个时候模型表现很差。识别出这些OOD数据很重要，比如对抗样本、异常检测。

传统的OOD检测方法是基于softmax confidence，即对于ID数据，模型会给一个高可信度的结果，对于可信度低的就是OOD样本。但是也可能会给OOD样本高可信度（比如对抗样本）。

这篇文章提出一个energy function来替换softmax函数识别OOD，ID样本能量低，OOD样本能量高。

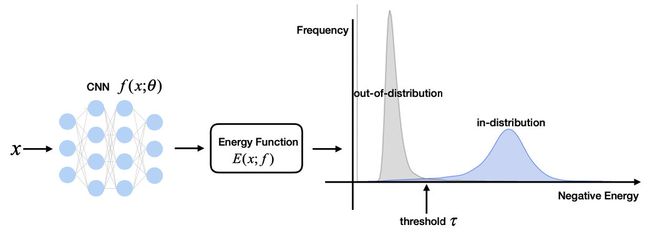
什么是能量模型（EBM）

能量模型最早由LeCun在2006年提出，本质构建一个能连函数$E(x):{\mathbb{R}}^D\to \mathbb{R}$，将输入空间的每个样本$x$映射到一个表示能量的非概率标量上。然后通过Gibbs分布可以将能量转化为概率密度：
$$p(y\mid \mathbf{x})=\frac{e^{-E(\mathbf{x},y)/T}}{{\int }_{y^{\prime }}{e}^{-E\left(\mathbf{x},y^{\prime }\right)/T}}=\frac{e^{-E(\mathbf{x},y)/T}}{e^{-E(\mathbf{x})/T}}\text{\hspace{1em}(1)}$$
其中分母被称为配分函数，$T$是温度参数。此时对于任意样本的能量$E(x)$为：
$$E(\mathbf{x})=-T\cdot \log {\int }_{y^{\prime }}{e}^{-E\left(\mathbf{x},y^{\prime }\right)/T}\text{\hspace{1em}(2)}$$
对于一个$K$类的神经网络分类器$f(x):{\mathbb{R}}^D\to {\mathbb{R}}^K$将输入映射到$K$个对数值，通过softmax得到当前样本属于某一类的概率：
$$p(y\mid x)=\frac{e^{f_y(x)/T}}{{\sum }_{i=1}^K{e}^{f_i(x)/T}}\text{\hspace{1em}(3)}$$
这里$f_y(x)$对应第$y$类标签的logit值。到这里我们可以将输入$(x,y)$的能量值表示为负的$f_y(x)$，这样就在原始神经网络分类器和能量模型之间建立起了联系，我们可以用softmax函数的分母来表示当前输入样本$x$的能量：
$$E(\mathbf{x};f)=-T\cdot \log \sum _i^K{e}^{f_i(\mathbf{x})/T}\text{\hspace{1em}(4)}$$
这里样本$x$的能量已经与样本的标签无关了，就是关于$f(x)$的一个标量。

基于能量的OOD检测

能量异常分数，行

OOD检测实际上是一个二分类问题，用能量函数来构建判别模型的密度函数：
$$p(\mathbf{x})=\frac{e^{-E(\mathbf{x};f)/T}}{{\int }_{\mathbf{x}}{e}^{-E(\mathbf{x};f)/T}}\text{\hspace{1em}(5)}$$
其中分母配分函数$Z={\int }_{\mathbf{x}}{e}^{-E(\mathbf{x};f)/T}$。上式取对数：
$$\log p(\mathbf{x})=-E(\mathbf{x};f)/T-\underset{\text{constant for all x }}{\log Z}\text{\hspace{1em}(6)}$$
上式表明$-E(x;f)$实际上与对数似然函数是线性对齐的，低能量意味着高似然(ID)，高能量意味着低似然(OOD)。那么设置一个阈值$\tau$就可以分类了：
$$G(\mathbf{x};\tau ,f)=\{\begin{array}{ll}0& \text{ if }-E(\mathbf{x};f)\le \tau \\ 1& \text{ if }-E(\mathbf{x};f)>\tau \end{array}\text{\hspace{1em}(7)}$$
其中阈值$\tau$是从正常样本数据分布统计得到的。

softmax函数，不行

文章里为什么要提上面“与似然函数线性对齐”的事呢？因为可以推出softmax置信分数对不齐。先推导出能量分数和softmax置信分数之间的联系：
$$\begin{array}{rl}\underset{y}{\max }p(y\mid \mathbf{x})& =\underset{y}{\max }\frac{e^{f_y}(\mathbf{x})}{{\sum }_i{e}^{f_i(\mathbf{x})}}=\frac{e^{f^{\max }(\mathbf{x})}}{{\sum }_i{e}^{f_i(\mathbf{x})}}\\ & =\frac{1}{{\sum }_i{e}^{f_i(\mathbf{x})-f^{\max }(\mathbf{x})}}\\ ⟹\log \underset{y}{\max }p(y\mid \mathbf{x})& =E\left(\mathbf{x};f(\mathbf{x})-f^{\max }(\mathbf{x})\right)=E(\mathbf{x};f)+f^{\max }(\mathbf{x})\end{array}\text{\hspace{1em}(8)}$$
把公式（6）带入，令$T=1$：
$$\log \underset{y}{\max }p(y\mid \mathbf{x})=-\log p(\mathbf{x})+\underset{\text{Not constant. Larger for in-dist }\mathbf{x}}{f^{\max }(\mathbf{x})-\log Z}\text{\hspace{1em}(9)}$$
这里后两项$f^{\max }(\mathbf{x})-\log Z$不是一个常数，相反，对于ID样本，其负对数似然期望是更小的，但是$f^{max}(x)$这个分类之心度却是越大越好，这二种冲突。这一定程度上解释了基于softmax confidence方法的问题。

能量边界学习

在相同模型上，能量函数已经比softmax函数好了，那要是能有针对性的fine-tuning一下就更好了。作者就提出了一种能量边界目标函数来fine-tuning网络：
$$\underset{\theta }{\min }{\mathbb{E}}_{(\mathbf{x},y)\sim {\mathcal{D}}_{\text{in }}^{\text{tain }}}\left[-\log F_y(\mathbf{x})\right]+\lambda \cdot L_{\text{energy }}\text{\hspace{1em}(10)}$$
其中第一项是标准的交叉熵损失函数，作用在ID训练数据上。第二项是一个基于能量的正则化项：
$$\begin{array}{rl}{L}_{\text{energy }}& ={\mathbb{E}}_{\left({\mathbf{x}}_{\text{in }},y\right)\sim {\mathcal{D}}_{\text{in }}^{\text{train }}}{\left(\max \left(0,E\left({\mathbf{x}}_{\text{in }}\right)-m_{\text{in }}\right)\right)}^2\\ & {+{\mathbb{E}}_{{\mathbf{x}}_{\text{out }}\sim {\mathcal{D}}_{\text{out }}^{\text{train }}}\max \left(0,m_{\text{out }}-E\left({\mathbf{x}}_{\text{out }}\right)\right))}^2\end{array}$$
惩罚能量高于$m_{in}$的ID数据和能量低于$m_{out}$的ODD数据，来拉远正常数据和异常数据分布之间的距离。

实验

实验是用SVHN、CIFAR-10和CIFAR-100作为正常样本数据集，另外六个OOD数据集。用WideResNet作为预训练模型。

总的结论就是：不fine-tuning的话好于softmax confidence的方法；fine-tuning的话好于目前的sota-OE方法（而且在ID数据上准确度不掉点）：

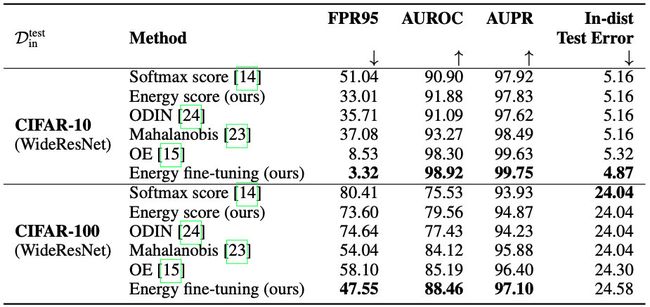
还有一个图我们很熟悉：

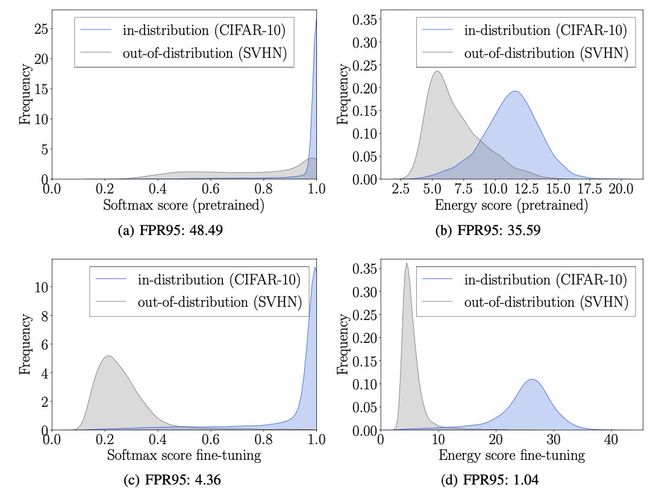
从两个分布的概率直方图上看，Energu score比Softmax score拉得开；energy score fine-tuning的方法比OE fine-tuning拉得开。