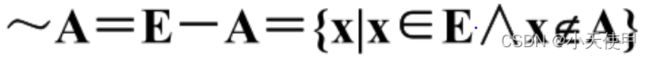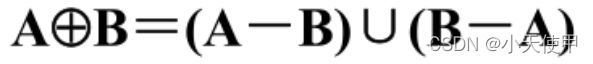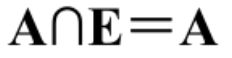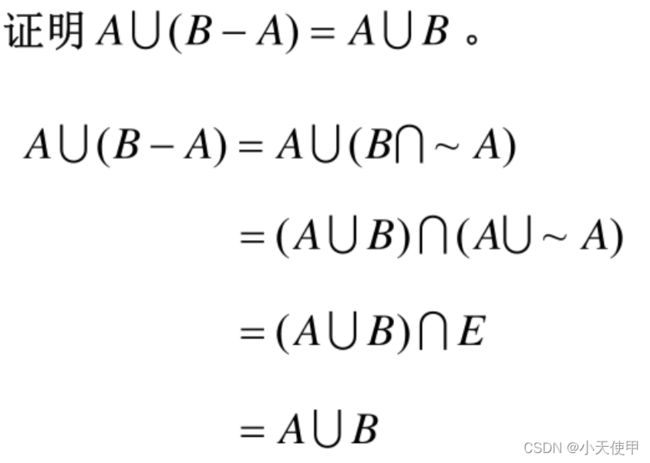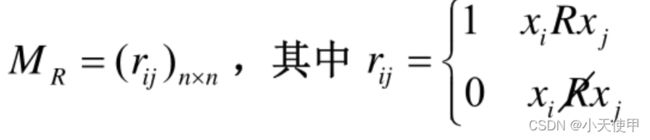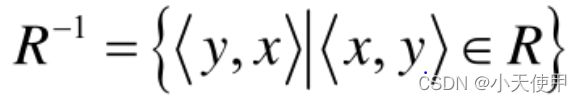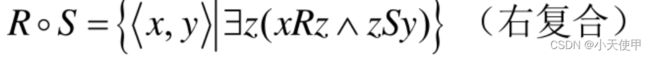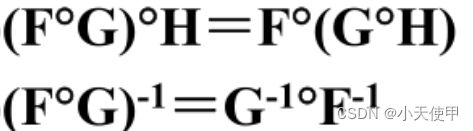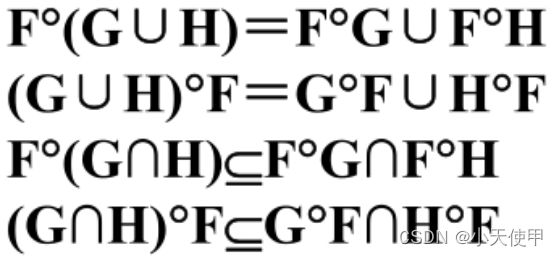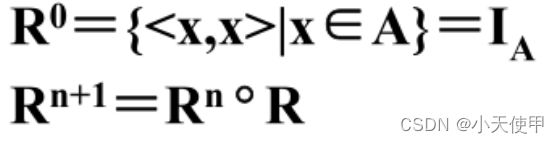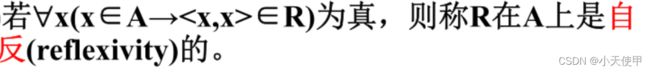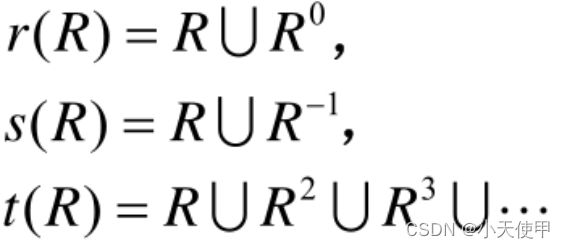离散数学笔记

目录

1. 命题逻辑

1.1. 命题：

1.2. 逻辑联结词（逻辑运算符）：将简单命题联结为复合命题

1.3. 复合命题符号化：

1.4. 命题公式：

1.5. 命题逻辑等值演算

1.6. 命题逻辑的推理理论

2. 一阶逻辑

2.1 一阶逻辑命题符号化

2.1.1. 个体词

2.1.2. 谓词

2.1.3. 量词

2.1.4. 命题符号化

2.2. 一些小概念

2.3. 合式公式的解释

2.4公式的类型

2.4.1逻辑有效式（永真式）

2.4.2矛盾式（永假式）

2.4.3可满足式

2.5一列逻辑等值演算与推理

3. 集合论

3.1 集合代数

3.1.1 基本概念

3.1.2 集合的运算

3.1.3 文氏图

3.1.4 有穷集的计数

3.1.5 集合恒等式

3.2 二元关系

3.2.1 有序对

3.2.2 笛卡儿积

3.2.3 二元关系

3.2.4 关系的运算

3.2.5 关系的性质

3.2.6 关系的闭包

3.2.6 等价关系和集合的划分

3.2.7 偏序关系

3.3 函数

3.3.1 函数基本概念

3.3.2 函数的性质

4. 图论

4.1 图的基本概念

4.1.1 无序积

4.1.2 无向图

4.1.3 有向图

4.1.4 n阶图

4.1.5 零图

4.1.6 空图

4.1.7 基图

4.1.8 简单图

4.1.9 多重图

4.1.10 度

4.1.11 握手定理

4.1.12 度数列

4.1.13 完全图

4.1.14 子图&母图

4.1.15 补图

4.1.16 图的同构

4.2 通路和回路

4.2.1 基本定义

4.2.2 表示方法

4.2.3 性质

4.2.4 无向图的连通性

4.2.5 有向图的连通性

4.2.6 二部图

4.3 图的矩阵表示

4.3.1 关联矩阵

4.3.2 有向图的邻接矩阵

4.3.3 计算题

4.4 欧拉图&哈密顿图

4.4.1 欧拉图

4.4.2 哈密顿图

5. 树

5.1 无向树

5.1.1 基本概念

5.2生成树

5.2.1 基本概念

5.2.2 生成树算法

5.2.3 最小生成树

5.2.4 求最小生成树

---

1. 命题逻辑

1.1. 命题：

真值唯一的陈述句，用小写字母表示。真值为真时用“1”或“T”表示，为假时用“0”，“F”表示。

1.2. 逻辑联结词（逻辑运算符）：将简单命题联结为复合命题

1.2.1. 否定negation

命题p的否定式为“非p”或“p的否定”，记作

1.2.2. 合取conjunction

复合命题“p并且q”称作p和q的合取式，记作,为真当且仅当（if and only if）p与q均为真。

1.2.3. 析取disjunction

复合命题“p或者q”称作p和q的析取式，记作，为真当且p或q为真。

1.2.4. 蕴涵implication

复合命题“如果p，则q”称作p和q的蕴含式，p为前件，q为后件，记作，为假当且仅当p为真，q为假。当p为假时，不管q为什么命题都为真。注意，数理逻辑中，p，q不需要一定有内在联系。

1.2.5. 等价two-way-implication

复合命题“p当且仅当q”称作p与q的等价式，记作。p与q互为充要条件

规定逻辑运算符的优先级顺序为1.1到1.5，即从否定到等价，有括号时先进行括号内的运算。

1.3. 复合命题符号化：

1.3.1. 找出各简单命题，分别符号化

1.3.2. 找出联结词，将简单命题联结成复合命题

1.4. 命题公式：

命题常项：真值确定的简单命题。

命题变项：真值不确定的陈述句，也可以用小写字母表示。

命题公式（合式公式）：由命题变项、联结词、括号等等组成的字符串。单个命题变项是合式公式，合式公式的否定式、析取式、合取式、等价式也是合式公式。

1.4.1. 命题公式的层次：

单个命题变项为0层公式。

若B是n层公式，A为B的否定式，则A为n+1层公式。

若B,C分别为i，j层公式，A为B和C的析取式、合取式或等价,即 ，且n=max(i,j)，则A为n+1层公式。

1.4.2. 公式的解释和赋值

给公式中所有的命题变项指定一个真值。若指定的一组真值使A的真值为1，则称这组值为A的成真赋值，否则称A的成假赋值。

1.4.3. 真值表

公式A在所有赋值下取值列成的表。

1.4.4. 重言式、可满足式、矛盾式

重言式（永真式）：命题无成假赋值

矛盾式（永假式）：命题无成真赋值

可满足式：至少存在一组成真赋值

1.5. 命题逻辑等值演算

1.5.1. 等值式

若命题公式A,B的等价式是重言式，则A与B等值，记作。

基本等值式：

 1.5.2. 等值演算

置换规则：若，则 。其中，为含A的命题公式。

等值演算的用处：证明两个公式等值；判断公式类型；简化公式。

1.5.3. 析取范式and合取范式

简单析取式和简单合取式：

有限个命题变项以及其否定构成的析取式或合取式。

极小项：

简单合取式中的每个命题变项和其否定不同时出现，且仅出现一次。出现顺序按角标或字典顺序。将每个极小项的成真赋值转化为十进制i，则记此极小项为。

极大项：

简单析取式中的每个命题变项和其否定不同时出现，且仅出现一次。出现顺序按角标或字典顺序。记为。

析取范式：由有限个简单合取式构成的析取式。

合取范式：由有限个简单析取式构成的合取式。

 求命题公式的等价范式步骤：

a.消去联结词；b.消去否定(双重否定)或内移否定(德摩根律)；c.利用分配律。

主析取范式：每个简单合取式都是极小项。

主合取范式：每个简单析取式都是极大项。
 

求命题公式A的主析取范式步骤：

a.求A的等价范式；b.补充变元；c.消去重复的以及永假项；d.按角标顺序排列

 续上

由主析取范式可以直接写出真值表。

有多少个极小项，则有多少个成真赋值。

而主合取范式由极大项组成，有多少个极大项，则有多少个成假赋值。

1.6. 命题逻辑的推理理论

有两种推理方法！！！！！将在下面的1.6.1和1.6.2中详细讲！！！

(1)

(2) 前提：A1,A2,...,Ak

     结论：B1

1.6.1. 推理的形式结构

若为重言式，则称前提A1,A2,A3推出结论B的推理正确。

可以直接用以下三类方法直接判断推理是否正确（命题数量较少的时候）。

(1). 真值表法：
即判断是否全是成真赋值。

若真值表最后一列全为1，则推理正确。

(2). 等值演算法：

 最后推出1，则显然推理正确。

(3). 主析取范式法：

若最后有个成真赋值m（n为命题个数），即主析取范式含所有极小项时，为重言式，推理正确。

 1.6.2. 构造证明法

(1). 推理定律（9条）：

 

(2). 推理规则：

a. 前提引入规则（前提可以在任何步骤引入）

b. 结论引入（前面步骤得出的结论可以作为后面步骤的前提）

c. 置换规则（在任何步骤，命题公式中的子公式都可以被与其等值的公式替换）

此外，由推理定律也可以得到9条对应的推理规则，这里略过。

(3). 自然推理系统中的构造证明法：

前提：A1,A2,...,Ak

结论：B1

证明方法：

a. 直接证明法

如下：

b. 附加前提证明法

当结论为形式时，可以将结论的前件作为前提，使得C为推理的结论。

如下：

 

c. 归谬法（反证法）

将结论的否定作为前提，推出矛盾，则可以证明结论的正确。

如下：

 

命题逻辑有它自己的局限性，因此，在它的基础上，我们继续讨论一阶逻辑

2. 一阶逻辑

2.1 一阶逻辑命题符号化

一阶逻辑将简单命题再细分，分析出个体词、谓词、量词，以刻画个体与总体之间的内在联系与数量关系。

2.1.1. 个体词

研究对象中可以独立存在的抽象或是具体的客体。（通常是主语的名词或代词）

(1). 个体常项

表示具体或特定客体的个体词，用小写字母a,b,c表示。如：小王是中国人。

(2). 个体变项

表示抽象或泛指客体的个体词，用x,y,z表示。如：x是有理数。

(3). 个体域（论域）

个体变项的取值范围。

其中，总体个体域由宇宙之间一切事物组成。推理总，若没有指明，则一律用总体个体域。

2.1.2. 谓词

用以刻画个体词性质以及个体词之间的相互关系。

如：命题“x是无理数”中，x是个体变项，“是无理数”是谓词，记为F。则此命题符号化为F(x)。

(1). 谓词常项

表示具体性质或关系的谓词。用大写字母表示。

(2). 谓词变项

表示抽象或泛指关系的谓词。用大写字母表示。

(3). n元谓词

含n个个体变项的谓词称作n元谓词，如P(x1,...,xn)。

注意：n元谓词不是命题，只有用谓词常项取代P，用个体常项取代x1,...xn时，才能使n元谓词变为命题。

(4). 0元谓词

不含个体变项的谓词。

2.1.3. 量词

表示数量的词。

(1). 全称量词

符号化为，表示个体域内所有个体。

(2). 存在量词

符号化为，表示存在个体域内的个体。

2.1.4. 命题符号化

理解前面的概念之后，我们就可以在一阶逻辑下进行命题符号化啦！

举个例子：

 

2.2. 一些小概念

(1). 项

个体常项、个体变项，以及有限个个体常项和个体变项的函数是项。

(2). 原子公式

x1,...,xn是项，F(x1,...,xn)是n元谓词，则称F(x1,...,xn)为原子公式。

(3). 合式公式

原子公式是合式公式。若A,B为合式公式，则A,B的否定、析取、蕴含、合取、等价式均为合式公式。

(4). 约束出现和自由出现

和中，x为指导变元，A为相应量词的辖域。

在量词的辖域中，指导变元x的所有出现均为约束出现。其他出现为自由出现。

 举个例子：

 (5). 闭式

即封闭的合式公式。

指无自由出现的个体变项的合式公式。

2.3. 合式公式的解释

对一阶合式公式中的各种变项，指定特殊的常项去替代，则构成了公式的一个解释。

解释I由四部分组成：

(1)非空个体域D

(2)D中一部分特定元素

(3)D中一些特定函数

(4)D中一些特定谓词

解释I下的赋值：

对自由出现的个体变项x指定D中一个值。

举个例子：

给定解释I如下

 则在解释I下，为假命题。

再举个例子：

给定解释N如下

上图 5中是对各个自由出现的个体变项的赋值哦。

注意：给定解释I和I下的赋值，任何公式都能被解释成命题。没有自由出现的个体变项的公式不需要赋值。

2.4公式的类型

2.4.1逻辑有效式（永真式）

2.4.2矛盾式（永假式）

2.4.3可满足式

命题公式中重言式、矛盾式、可满足式的代换实例在一阶逻辑中仍然是重言式、矛盾式、可满足式。

2.5一列逻辑等值演算与推理

2.5.1一阶逻辑等值式定义

A,B为两个命题公式，若是逻辑有效式，则称A,B是等值的。记作，称作等值式。

2.5.2重要等值式

(1)代换实例

(2)消去量词等值式

(3)量词否定等值式

(4)量词辖域收缩与扩张等值式

(5)两次分配等值式

3. 集合论

3.1 集合代数

3.1.1 基本概念

(1) 集合

一些确定的对象的整体，用大写字母表示，集合内的对象称作元素。

(2) 集合的表示方法

a. 列举法

b. 谓词表示法

(3) 集合间的关系

a. 包含

b. 相等

c. 子集

d. 空集

(4) 幂集

集合A全体自己构成的集合，记作P(A)。

(5) 全集

某具体问题中，所有集合均是某个集合的子集，则该集合为全集。

3.1.2 集合的运算

(1) 交集

(2) 并集

 推广：

n个集合的交与并预算

(3) B对A的相对补集

(4) 绝对补集

(5) 对称差集

 另一种等价的定义是

3.1.3 文氏图

(1) 大矩阵表示全集E

(2) 圆形表示集合

3.1.4 有穷集的计数

(1) 基数：集合含有的元素个数可以称作集合的基数，记作card A=n或 |A|=n。

(2) 有穷集：包含有限个元素的集合

(3) 有穷集的计数方法

a. 文氏图法

b. 包含排斥原理

3.1.5 集合恒等式

(1) 恒等式

 

 

(2) 集合恒等式的证明方法

a. 逻辑演算法

格式如下：

举个例子：

要证明

b. 集合演算法

 举个例子：

3.2 二元关系

3.2.1 有序对

由两个对象a,b按一定次序组成的二元组称为一个有序对，记作(a,b)，a为其第一元素，b为其第二元素。

3.2.2 笛卡儿积

若A,B为集合，所有以A中元素为第一元素，B中元素为第二元素构成的有序对组成的集合称作A,B的笛卡儿积。记作。

特点：

不满足交换律、结合律，但对或满足分配律。

3.2.3 二元关系

(1) 若A,B为集合，的子集R称作A到B的一个二元关系，简称关系。

(2) 集合A上的二元关系数目

若|A|=n，则，则的子集有个，因此，有个二元关系。

(3) 特殊的关系

对任何集合A，

 (4) 常用关系

 (5) A上二元关系的表示法

a. 集合表示法

b. 关系矩阵表示法

（可以表示A到B的关系，也可以表示A上的关系）

若集合A上有关系R，则关系矩阵 如下表示：

c. 关系图表示法

（只合适表示A上的关系）

若集合A上有关系R，且|A|=n，则关系图如下表示：

举个例子：

3.2.4 关系的运算

(1) 关系的定义域

二元关系R中所有有序对第一个元素构成的集合称作R的定义域，记作dom R。

(2) 关系的值域

二元关系R中所有有序对第二个元素构成的集合称作R的值域，记作ran R。

(3) 关系的域

关系的定义域和值域并称为关系的域，记作fld R。

(4) 关系的逆

(5) 关系的合成

关系R和S的合成定义成：

 

 我们这里都用右复合。

(6) 关系的限制和像

(7) 运算的规律

若F,G,H为任意二元关系，则

(8) 关系的幂运算

(9) 的计算

a. 通过n-1次右复合运算即可。

b. 若R用关系矩阵M表示，则只需要求n个关系矩阵之积。

c. 若R用关系图表示，则

 举个例子：

3.2.5 关系的性质

若R为A上的关系。

(1) 自反性

关系矩阵的特点：对角线上均为1

(2) 反自反性

关系矩阵的特点：对角线上均为0

(3) 对称性

关系矩阵为对称矩阵。

(4) 反对称性

 关系矩阵特点：若 ，则。

关系图特点：若两点间有边，必是一条有向边。

(5) 传递性

 关系矩阵的特点：对应M2上1的位置，M上也是1。

(6) 性质的判别方法

3.2.6 关系的闭包

(1) 若R是A上的关系，R的自反闭包(对称闭包，传递闭包)R'也是A上的关系，且满足：

a. R'是自反的(对称的，传递的)

b.

c. 对A上，任何包含R的自反关系R''，都有

记作r(R)——自反闭包；s(R)——对称闭包；t(R)——传递闭包。

(2) 闭包的求法

a. 关系图法

自反闭包的关系图Gr，考察每个顶点，若没有环则加上一个。

对称闭包的关系图Gs，若存在xi到xj的单向变()，则加上xj到xi的单向边。

传递闭包的关系图Gt，考察每个顶点，找出从顶点出发的每一条路径。

b. 公式法

c. 关系矩阵法

若R,r(R),s(R),t(R)的关系矩阵分别为M,Mr,Ms,Mt，M的转置矩阵为M'。

3.2.6 等价关系和集合的划分

(1) 等价关系的定义

若A上的关系R满足自反、对称、传递，则称R为A上的等价关系。若 ，记x~y。

(2) 等价类

若R为非空集合A上的等价关系，对 ，记 为x关于R的等价类。

x的等价类是由A中所有与x等价的元素构成的集合。

性质：

(3) 商集

R为等价关系，以R的不交的等价类作为元素的集合叫做A在R下的商集，记作A/R，

(4) 集合的划分

若A为一个非空集合，其子集族m ( ) 满足下面的条件：

则称m为A的一个划分，m中的元素称作划分块。

集合A上的等价关系与集合A的划分是一一对应的。即一个等价关系可以确定一个划分，反之亦是

3.2.7 偏序关系

(1) 偏序关系的定义

这里的“小于等于”指的是偏序关系中的顺序性。

(2) 偏序集

集合A与集合A上的偏序关系R一起称作偏序集，记作。

举个例子：

集合A上的恒等关系：>

(3) 可比和盖住

举个例子：

(4) 全序集

若为偏序集，A中任意x,y均可比，则称R为A上的全序关系，称为全序集。

举个例子：

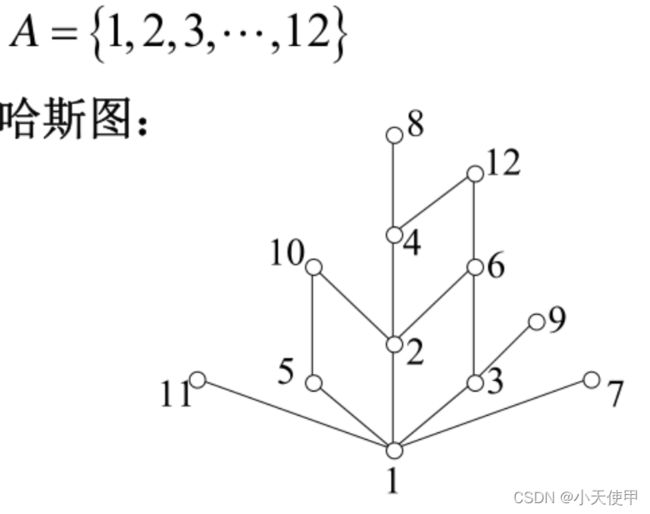
(5) 哈斯图

利用偏序关系的自反性、反对称性以及传递性得到的图。

作图步骤：

举个例子：

(6) 偏序集相关基本概念

注意是所有的x均要“小于等于”y，不可以存在不可比的情况，即只能有一个最大最小元。

注意极大极小元，只需要不存在比y小或大的即可，可以存在不可比的情况，即多个极大极小元。

注意上界下界上确界下确界均不一定存在，然而上界下界可能有很多个，但上确界下确界只能有一个。y必须和每个x都可比！

3.3 函数

函数是特殊的二元关系。

3.3.1 函数基本概念

(1) 函数定义

若F为二元关系，对任意，都存在唯一的，使得xFy成立，则称F为函数。函数记号为大写或小写的字母。

(2) 函数的相等

(3) 函数的定义域、值域

设A,B为集合，若函数 f 满足 dom f=A，ran f=B，则称f为从A到B的函数，记作 。

(4)

 注意：ran f 包含于 B，而不必等于B。dom f 等于A。

(5) 函数的像

若f为一个函数，且 ，则称f(A1)为A1在f下的像，f(A1)是一个集合，且。

3.3.2 函数的性质

(1) 满射：则ran f=B。

(2) 双射：

(3) 单射：若f既是满射又是双射则称单射。

4. 图论

4.1 图的基本概念

4.1.1 无序积

若A,B为两个集合，则称A&B={ {a,b} | }为A与B的无序积。可将无序积中的无序对{a,b}记作(a,b)。

4.1.2 无向图

一个无向图是一个有序的二元组，记作G。V称作顶点集，非空，其中的元素称作点；E称作边集，是无序积V&V的多重子集，其中元素称作无向边。

4.1.3 有向图

一个有向图是一个有序的二元组，记作D。E称作边集，是笛卡儿积的多重子集，其中的元素称作有向边。

一般用E(G)表示边集，用V(G)表示点集。

4.1.4 n阶图

若|V(G)|=n，则称G为n阶图。

4.1.5 零图

若E(G)为空集，则称G为零图。

4.1.6 空图

原本是规定顶点集不可以是空集，但是运算中可能会出现顶点集为空集的情况，所以就规定顶点集为空集时称为空图。记作。

4.1.7 基图

将有向图中的有向边化作无向边之后的图称作原图的基图。

4.1.8 简单图

无向图中，关联一对顶点的无向边多过一条则称为平行边，平行边数量称作重数。

有向图中，关联一对顶点且方向相同的边称作平行边。

不含平行边也不含环的称作简单图。

4.1.9 多重图

含有平行边的称作多重图。

4.1.10 度

无向图中，点v作为边的端点的次数之和称作v的度数，简称度。记作d(v)。

有向图中，点v作为始点次数之和称作v的出度，记作d+(v)。点v作为终点次数之和称作v的入度，记作d-(v)。而称入度与出度之和为v的度数，记作d(v)。

另外，称度数为1的顶点为悬挂顶点，与其关联的为悬挂边。度数为偶数的称偶度顶点，奇数的称奇度顶点。

4.1.11 握手定理

任意无向图各顶点的度数总和为边数的两倍。

任意有向图各顶点的度数总和也为边数的两倍，入度总和和出度总和等于边数。

推论：任意图中，度数为基数，则顶点为偶数。

4.1.12 度数列

对无向图G=，若V={v1,v2,...,vn}，则d(v1),...,d(vn)为G的度数列。对标定了顶点的无向图而言度数列唯一。

有向图也类似无向图存在度数列，以及出度列，入度列。

4.1.13 完全图

若G为n阶无向简单图，若每个端点均与其余n-1个端点相邻，则称G为n阶无向完全图，记作Kn。

若D为n阶有向简单图，对任意顶点v,u，既存在，又存在，则称D为n阶有向完全图。

若D为n阶有向简单图，且D的基图为n阶无向完全图，则D称作竞赛图。

 

4.1.14 子图&母图

(1) 子图和母图

若G=，G1=（同时为无向图或者有向图），有，则G1为G的子图，G为G1的母图。记作。

(2) 生成子图

在此基础上，若V1=V，则称V1为V的生成子图。

(3) 导出子图

若G=，且不为空集，则以V1为点集，以G中两端点均在V1中的边组成边集E1，则G1=为G的V1导出的导出子图，记作G[V1]。

若G=，且不为空集，则以E2为边集，以E1中的边所关联的顶点组成点集V2，则G2=为G的E2导出的导出子图，记作G[E2]。

4.1.15 补图

若G为n阶简单图，则所有使G成为完全图的添加边的集合为边集的图称作补图。

4.1.16 图的同构

必要条件：结点数相同，边数相同，度数相同的结点数量相同。

4.2 通路和回路

4.2.1 基本定义

若G为无向图。

(1) 通路

G中顶点与边的交替序列L=v0e1v1e2...envn称作v0到vn的通路，vn,vn称作L的始点与终点，L中边的总数称作L的长度。

(2) 回路

若v0=vn，则L为回路。

(3) 简单通路&简单回路

若L中所有边各异，则L称作简单通路；若在此基础上v0=vn，则L为简单回路。

(4) 初级通路

若L中所有顶点各异，所有边各异，则L称作初级通路或者路径。

(5) 初级回路

若L中所有顶点各异，所有边各异，且v0=vn，则L称作初级回路或者圈。

(6) 复杂通路

若L中有边重复出现，则L称作复杂通路。

(7) 复杂回路

若L中有边重复出现，且v0=vn，则L称作复杂回路。

若D为有向图，通路和回路的定义与无向图无甚差别，但要注意有向边方向的一致性。

4.2.2 表示方法

(1) 用边的序列表示通路或回路

(2) 用点的序列表示通路或回路（简单图）

4.2.3 性质

若G为n阶图，若vi到vj(i不等于j)之间存在通路，则一定存在长度小于等于n-1的通路。若存在vi到自身的回路，则一定存在长度小于等于n的回路。

4.2.4 无向图的连通性

(1) 连通

若G为无向图，点u,v之间存在通路，则称u,v之间是连通的。记作u~v。

规定对于G中任意点v，存在v~v。

(2) 连通关系

无向图顶点之间的联通关系记作：~={(u,v)|u,v属于G的点集且u,v是连通的}

连通关系是点集V上的等价关系。

(3) 连通图

若图G中任两个顶点间都是连通的，则可以称作连通图（如完全图），否则称作非连通图或者分离图。

(4) 连通分支

若无向图G=，商集V/~={V1,...Vk}，Vi为等价类，称导出子图G[Vi]为G连通分支，连通分支数k记作p(G)。

如果G是连通图，则p(G)=1。

(5) 距离

称u,v之间最短的通路为短程线，短程线的长度称距离，记作d(u,v)。若u,v不连通时，记d(u,v)=

4.2.5 有向图的连通性

若D=为一有向图。

(1) 可达

点u,v属于点集V，若u到v之间存在通路，则称u可达v，记作。若v也可达u，则称u,v是相互可达的，记作。

规定，点v总是可达自身的。

(2) 距离

若，称u到v的最短通路为短程线，短程线的长度称作距离。记作d。

(3) 连通图

若D的基图为连通图，则称D为弱连通图，简称为连通图。

若任意两点u,v存在或者，则称D为单向连通图。

若存在，则称D为强连通图。

判定：

D是强连通图当且仅当存在经过每个顶点至少一次的回路。

D是单向连通图当且仅当存在经过每个顶点至少一次的通路。

4.2.6 二部图

(1) 二部图

若无向图G=点集V存在两个子集V1,V2，V1和V2的并是V，交是空集，且G中每一条边的一个端点属于V1，另一个属于V2。则称G为二部图。

(2) 完全二部图

若V1中每一个点均和V2中所有点有且仅有一条边相连接，则称G作完全二部图。

二部图不一定是连通图

(3) 二部图的判定

G为二部图当且仅当G没有长度为奇数的回路

4.3 图的矩阵表示

4.3.1 关联矩阵

(1) 无向图的关联矩阵

若无向图G=，V={v1,...,vn}，E={e1,...,em}，令mij为顶点i与边j的关联次数，则称(mij)n*m为G的关联矩阵，记作M(G)。

(2) 有向图的关联矩阵

若有向图D=中无环，有向边ej的方向朝向vi，则记作mij=-1，若是反方向则记作mij=1。

4.3.2 有向图的邻接矩阵

若有向图D=，令aij为顶点vi邻接顶点vj的条数。称(aij)n*n为邻接矩阵，记作A(D)。

4.3.3 计算题

4.4 欧拉图&哈密顿图

4.4.1 欧拉图

(1) 欧拉通路

通过图中所有边一次且仅一次行遍图中所有顶点的通路。

是经过图中所有的边的通路中最短的一条。

(2) 欧拉回路

通过图中所有边一次且仅一次行遍图中所有顶点的回路。

是经过图中所有的边的回路中最短的一条。

(3) 欧拉图

具有欧拉回路的图称作欧拉图。具有欧拉通路而无欧拉回路的称作半欧拉图。

(4) 欧拉图的判定

若G为无向图，D为有向图。

G是欧拉图当且仅当G是连通图且G中无奇度顶点。

G是半欧拉图当且仅当G为连通图且G中恰有两个奇度顶点。

D是欧拉图当且仅当G为强连通图且每个点的出度等于入度。

D是半欧拉图当且仅当G为单向连通图且仅有两个奇度点，且一个的出度大入度1，一个入度大出度1。

(5) 求欧拉回路——Fleury算法

4.4.2 哈密顿图

(1) 哈密顿回路

经过所有顶点一次且仅一次的回路称作哈密顿回路。

(2) 哈密顿通路

经过所有顶点一次且仅一次的通路称作哈密顿通路。

(3) 哈密顿图

具有哈密顿回路的称作哈密顿图，仅具有哈密顿通路的称作半哈密顿图。

(4) 判定哈密顿图的必要条件

规定，平凡图是哈密顿图也是欧拉图。

(5) 判定哈密顿图的充分条件

若G为n阶无向简单图，对于任意不相邻的点，度数之和都大于等于n-1，则G中存在哈密顿通路。

若度数之和都大于等于n，则G中存在哈密顿回路。

若D为n阶竞赛图，则D中存在哈密顿通路。

(6) 有关二部图的哈密顿图判定

若二部图G=，|V1|<=|V2|，且|V1|<=2，|V2|<=2。

G是哈密顿图当且仅当|V1|=|V2|。

G是半哈密顿图当且仅当|V2|<=|V1|+1。

当|V2|>|V1|，G不是哈密顿图也不是半哈密顿图。

5. 树

树中没有环和平行边，因此，一定是简单图。

5.1 无向树

5.1.1 基本概念

(1) 无向树

连通无回路的无向图，简称树，可以用T表示

(2) 平凡树

即平凡图

(3) 森林

每个连通分支均为树的无向图

(4) 树叶

即悬挂顶点

(5) 分支点

度数大于等于2的顶点

(6) 树的特点

树若含有n个点，则一定含有n-1条边。树是边数最少的连通图，边数最多的无回路图。任意n阶非平凡的无向树T至少含有两片树叶。

5.2生成树

5.2.1 基本概念

5.2.2 生成树算法

若存在连通G=，V={v1,...vn}，E={e1,...,em}。

(1) 破圈法

找到图中的回路并删除回路的一条边，直到删除的边的总数为m-n-1

(2) 避圈法

循环选取一条与已选边不构成回路的边，直到选择的边总数为n-1

5.2.3 最小生成树

若T是一无向连通带权图G=的一个生成树。

T的各边权之和称作T的权，记作W(T)。

G的所有生成树中权最小的称作最小生成树。

5.2.4 求最小生成树

避圈法（Kruskal）

在与已选取的边不构成回路的边中取权最小的。