【分布外检测】《Deep Anomaly Detection with Outlier Exposure》 ICLR‘19

利用异常数据集训练异常检测器，这种方法称为异常暴露（Outlier Exposure，OE）。这使异常检测器能够泛化和检测未见的异常。在大量自然语言处理以及小规模和大规模视觉任务的广泛实验中，文章发现Outlier Exposure可显着提高检测性能。

Outlier Exposure

所谓异常暴露，就是给异常检测器引入异常数据，让模型能从已有的异常数据中获得启发，从而能泛化出未曾见过的异常。

这篇文章只有一个公式，即模型引入OE后的优化目标：
$${\mathbb{E}}_{(x,y)\sim {\mathcal{D}}_{\text{in }}}\left[\mathcal{L}(f(x),y)+\lambda {\mathbb{E}}_{x^{\prime }\sim {\mathcal{D}}_{\text{out }}^{\text{OE }}}\left[{\mathcal{L}}_{\mathrm{O}\mathrm{E}}\left(f\left(x^{\prime }\right),f(x),y\right)\right]\right]$$
其中第一项是$\mathcal{L}$原模型在原任务上的优化目标，第二项${\mathcal{L}}_{OE}$是OE优化目标，根据不同的任务而定，下面的实验就挨个定义。

数据集

IN-DISTRIBUTION DATASETS：SVHN、CIFAR、Tiny ImageNet、Places365、20 Newsgroups、TREC、SST。其中一个作为ID数据集时，另外同类数据集作为ODD。

OUTLIER EXPOSURE DATASETS：80 Million Tiny Images、ImageNet-22K、WikiText-2。剔除了和ID数据集重合的部分，保证${\mathcal{D}}_{\text{out }}^{\text{OE }}$和${\mathcal{D}}_{\text{out }}^{\text{test }}$正交。

任务一：多分类任务

对于一个k分类任务，输入$x\in \mathcal{X}$，分类器输出$y\in \mathcal{Y}=\{1,2,\dots ,k\}$。分类器$f:\mathcal{X}\to {\mathbb{R}}^k$，且对于任意$x$，$1^{\top }f(x)=1$ and $f(x)⪰0$。

Maximum Softmax Probability (MSP)

baseline。输入一个$x$，输出OOD得分${\max }_c{f}_c(x)$。

fine-tuning目标是：
$${\mathbb{E}}_{(x,y)\sim {\mathcal{D}}_{\text{in }}}\left[-\log f_y(x)\right]+\lambda {\mathbb{E}}_{x\sim {\mathcal{D}}_{\text{ot }}^{\text{oE }}}[H(\mathcal{U};f(x))]$$
其中$H$是交叉熵，$\mathcal{U}$是k类的均匀分布。

其实从一开始训练模型时就加入OE正则项效果更好，之所以选择fine-tuning是考虑时间和GPU内存。

加了OE的MSP方法在CV和NLP效果提升：

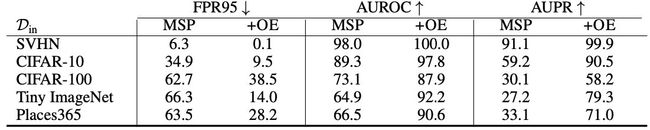
Confidence Branch

《Learning confidence for out-of-distribution detection in neural networks》2018中提出的方法，学习confidence，对于一个样本模型输出一个OOD分数$b:\mathcal{X}\to [0,1]$。那么这里用上OE就是在原模型的优化目标上加上：
$$0.5{\mathbb{E}}_{x\sim {\mathcal{D}}_{\text{out }}^{\text{OE }}}[\log b(x)]$$
效果：

Synthetic Outliers

作者想用OE来解决对抗样本，于是作者尝试用一些噪音扰乱图片，然后将这些加噪图片作为OE数据集。但是作者发现这样分类器虽然能记住这些噪音特征，但是不能识别新的OOD样本。然后作者直接用了一个别人的代码《Training confidence-calibrated classifiers for detecting out-of-distribution samples.》即在MSP的基础上用GAN fine-tuning，即对于GAN生成的样本给予一个高的OOD分数。然后作者在此基础上又用OE fine-tuning，效果进一步加强。具体这一部分怎么实现的细节我也没看太明白，这一部分篇幅短，也没有附录。

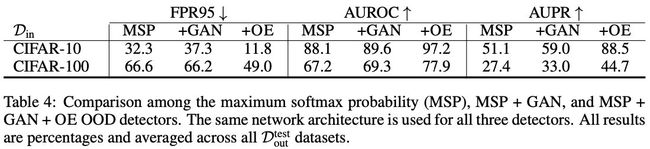
任务二：密度估计

密度估计器学习数据分布${\mathcal{D}}_{\text{in }}$上的概率密度函数，异常样本应该具有更低的概率密度，因为他们很少出现在${\mathcal{D}}_{\text{in }}$。

Pixel CNN++

一个样本$x$的OOD score用bits per pixel(BPP)表示为nll(x)/num_pixels，其中nnl是negative log-likelihood。这里OEis implemented with a margin loss over the log-likelihood difference between in-distribution and anomalous examples。那么来自${\mathcal{D}}_{in}$的样本$x_{in}$和来自${\mathcal{D}}_{\text{out }}^{\text{OE }}$的异常点$x_{out}$的loss是：
$$\max \left\{0,\text{ num\_pixels }+\mathrm{nll}\left(x_{\text{in }}\right)-\mathrm{nll}\left(x_{\text{out }}\right)\right\}$$

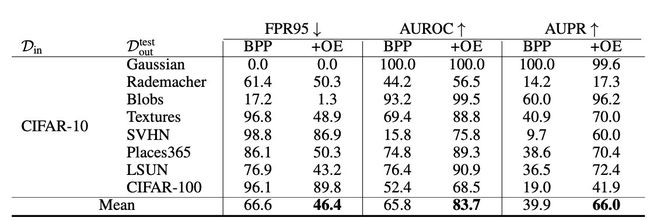
Language Modeling

用QRNN作为baseline OOD detectors。OOD score用bits per character (BPC) or bits per word (BPW)，定义为nll(x)/sequence_length。其中nnl($x$)是序列$x$的negative log-likelihood。OE通过adding the cross entropy to the uniform distribution on tokens from sequences in ${\mathcal{D}}_{\text{out }}^{\text{OE }}$ as an additional loss term实现。

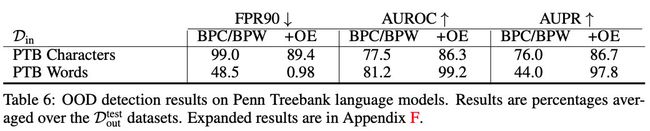
小结

作者提出的OE有很多优点，其中作者给出的结论有：可扩展性（很多任务都可以用）、可以灵活的选择${\mathcal{D}}_{\text{out }}^{\text{OE }}$、OE可以提高模型本身的精度等。

但是我觉得作者说的“${\mathcal{D}}_{\text{out }}^{\text{OE }}$可以让模型获得启发，从而泛化和识别没有见过的${\mathcal{D}}_{\text{out }}^{\text{test }}$”有些太玄乎了，毕竟分布这种东西人没办法准确的划分清楚，本质上有些像“Transfer Unlearning”。

我觉得这篇文章的优点是大量、翔实的实验，不多讲故事，每个点都用实验解释清楚。