NAS-based on cell DARTS
参考链接:
https://blog.csdn.net/zxfhahaha/article/details/102747427
https://blog.csdn.net/byron123456sfsfsfa/article/details/89930990
https://blog.csdn.net/weixin_42765656/article/details/109598194
https://zhuanlan.zhihu.com/p/73037439
https://zhuanlan.zhihu.com/p/143574526
1、先入为主
1.1什么是NAS
神经网络结构搜索(NAS)的原理是给定一个称为搜索空间的候选神经网络子结构集合,用某种策略从中搜索出最优的全局神经网络结构。神经网络结构的优劣即性能用某些指标如精度、速度来度量,称为性能评估。其结构可以用下图来衡量:
在每次结构搜索的迭代过程中,算法从搜索空间中选一个子结构,在训练集上训练该子网络,并在验证集上评估效果,接着通过搜索策略循环优化并找到最优的网络结构。
搜索空间定义了网络解的集合,搜索策略定义了以何种方法去寻找最优解,性能评估定义了怎样的网络结构是最优的。
传统的NAS方法大多基于强化学习(RL)或者遗传算法作为搜索的策略,基于离散的搜索空键进行黑箱优化,往往耗时巨大。
1.2可微结构搜索
本文提出了全新的可微结构搜索算法(Differentiable Architecture Search),将搜索空间连续化处理,便于用梯度下降等连续优化算法求解最优网络结构。
该算法提出了一个新的参数 α \alphaα 用于表征网络结构,即该向量代表了最终网络各子结构之间的连接方式。连续结构的单次迭代分两部分:
- 在训练集中搜寻最优的结构参数 α,并生成对应网络;
- 在验证集中应用该网络训练常规参数 w ,并评估效果。
最后由结构参数 α 生成离散结构作为最终的神经网络。
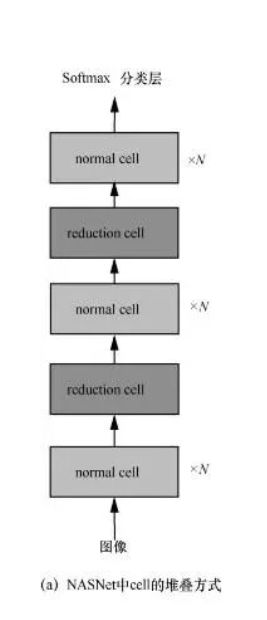
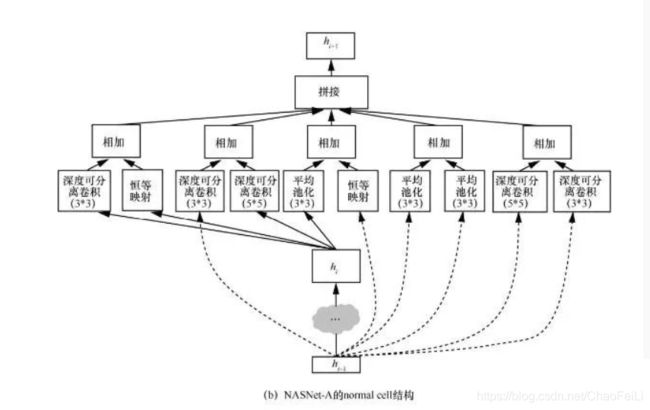
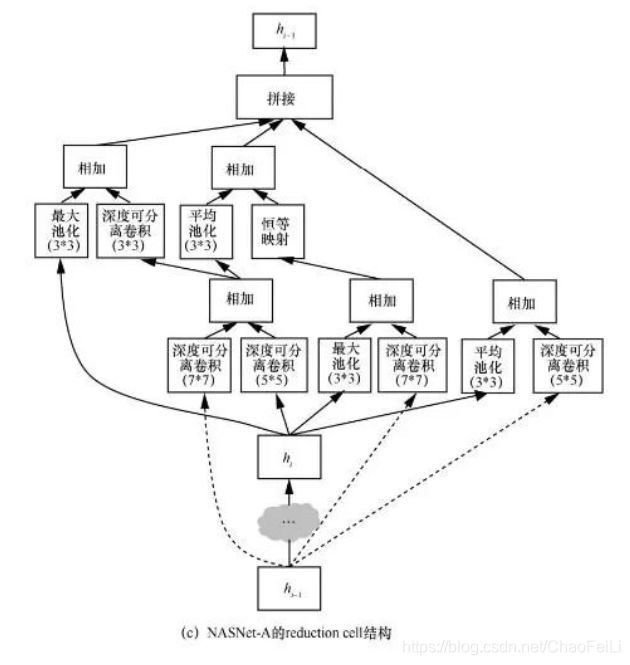
很多人工设计的神经结构是由重复的结构单元组成的,例如:ResNet结构由多个残差单元组成,GoogLeNet结构由 Inception 结构单元组成。由此启发,NAS 算法通过搜索结构单元(cell)来替代搜索整个神经结构。NASNet提出了基于cell结构的搜索空间。在这种搜索空间中,NAS算法搜索2种类型的cell,一种为normal cell,另一种为reduction cell。normal cell的输出和输入尺寸保持一致,而reduction cell的输出尺寸是输入尺寸的一半。在搜索完 cell 之后,再按照预先设定的方式堆叠这2种cell来构建完整的神经结构。图3(a)展示了 NASNet中的cell堆叠方式。在堆叠过程中normal cell重复堆叠N次,N的大小由人工设定。NASNet搜索出了NASNet-A、NASNet-B、NASNet-C 3种神经结构。图3(b)展示了NASNet-A中的normal cell结构。图3(c)展示了NASNet-A中的reduction cell结构。
上图所示:每个cell都有两个输入cell k-2和cell k-1,这2个输入可以来自网络中更浅的cell的输出,也可以来自图像数据。每个cell包含B个操作块(block),典型的B设置为5。每个block包含2个神经网络操作,在NASNet中,有13种操作可以被选择,例如卷积核长宽为 3 的卷积操作、卷积核长宽为1的卷积操作。在每个block中,这2个操作的输入可以从hi、hi-1以及前面的block的输出中选择,这2个操作的输出可以通过相加(add)或者拼接(concat)的方式来作为该block的输出。在搜索过程中,5个block按顺序逐个搜索,当5个block都搜索完成后,这5个block的输出中没有被使用过的输出会被拼接在一起作为cell的输出。虽然NASNet中有13种操作选项,但其中有5种在搜索出的cell中没有被选中过。因此,为了进一步缩减搜索空间,PNASNet将每个 block中可选的操作选项由 13种缩减到了8种。
基于cell结构的搜索空间有以下两点优势。
▪缩小了搜索空间,加速了神经结构的搜索过程。和搜索整个神经结构相比,只搜索2种cell结构可以减小NAS算法的搜索时间。
▪神经结构的深度可以灵活地扩展。当搜索出了最优的cell结构后,通过调整cell的堆叠数量,可以灵活地控制神经结构的深度和复杂度以适应不同的应用场景。例如, NASNet和 BlockQNN通过增大堆叠次数N 成功地利用在CIFAR-10上搜索出的cell结构构建出了在ImageNet数据集上性能优越的神经结构。
虽然基于cell的搜索空间被广泛应用于NAS算法,但通过 cell 堆叠整体神经结构的方式依然需要人工的设计和优化。这种堆叠方式可以认为是一种元结构(meta-architecture)。在未来,元结构的设计也应作为NAS算法的一部分。
2、循序渐进
2.1搜索空间
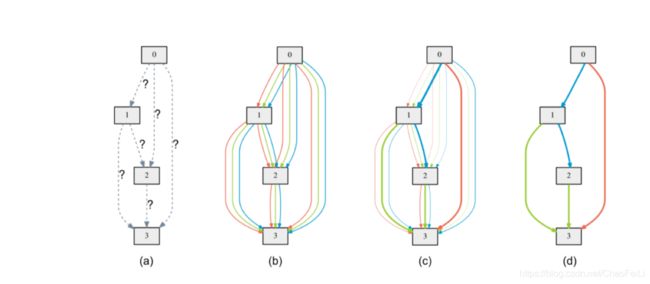
(a)这些灰色的小方块block都是一个cell内的nodes,我们需要通过一些操作(如池化、卷积)把这些nodes连起来
(b)原本一个个操作都是离散的,我们为了实现可微分的搜索,也就是为了使搜索空间连续,我们将特定操作的确定的选择放宽到所有可能操作上的softmax,也就是我们给两个block之间的全部操作都赋予权重。假设我们有三个操作,我们把每个节点都通过上述方法和它所有的前驱节点相连,就得到了下图(b)
然后我们就通过梯度下降对权重进行优化,最后对每个节点取argmax也就是哪个操作的α值最大,就选这个操作。
(d)选了最大的α后的操作后,我们就得到了(d)的路径
具体的在CIFAR-10定义网络结构我们可以看下图:
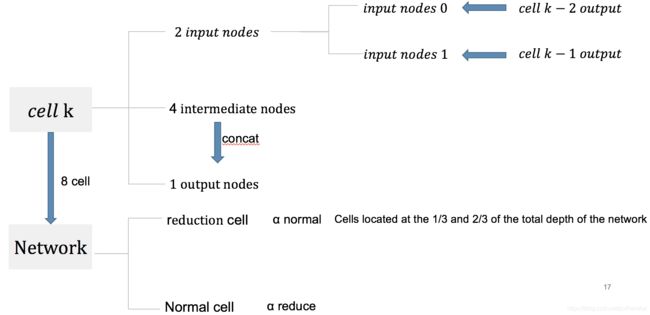
一个Network是由8个cell组成的,cell分为reduction cell 和normal cell两种,在网络的三分之一处和三分之二处是reduction cell,其它是normal cell。reduction cell共享权重α redution,normal cell共享权重
α normal。
一个cell由7个nodes组成,分别是2个input nodes,4个intermediate nodes和1个output nodes。
- input nodes:是前两层cell的输出,input node 0是cell k-2的输出,input node 1 是cell k-1的输出
- intermediate nodes:和它所有的前驱节点相连,具体看下面的公式
对于节点x ( j ) ,通过操作o和它所有的前驱节点i相连
- output nodes:四个中间节点intermediate nodes concat,这个concat是对通道concat的,也就是原来输入的通道是C,输出以后变成了4C
DARTS中的基本结构是Cell,整个网络主体由若干Cell连接而成。Cell分为两种,Normal cell和Reduction Cell。每个同类型Cell的结构相同且共享权重,其内部由若干节点(node)组成,每个节点可以看作一个表示(representation)或者特征图(feature map)。Cell由2个输入节点,一个输出和若干中间节点组成。中间节点与前序节点(包括之前的中间节点以及2个输入节点)的连接关系可以表示为:
# genotypes.py
PRIMITIVES = ['none', 'max_pool_3x3', 'avg_pool_3x3', 'skip_connect', 'sep_conv_3x3',
'sep_conv_5x5', 'dil_conv_3x3', 'dil_conv_5x5']
这些操作的集合构成了操作空间 O OO,上述公式具体在搜索过程和测试过程中有所不同。
2个输入节点分别与前2个Cell的输出相连,中间节点与前序节点相连,所有中间节点在通道维度上的concat构成了输出节点。