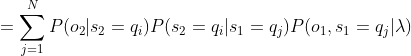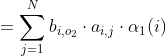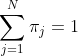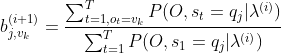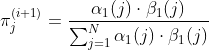语音识别与隐马尔可夫模型(HMM)

 

目录

一、语音识别

二、隐马尔可夫模型

三、前向—后向算法

四、Baum-Welch算法

五、孤立词识别

---

       公元2035年，机器人在人类社会中充当着十分重要的角色，它们可以送快递，为人类提供家政服务，甚至帮主人可以遛狗……这是电影《机械公敌》中的场景，这要是放在十几年前，可能还是有点异想天开，但是现在，原先的很多设想都已经初步实现了，例如可以跟人对话的聊天机器人，某些酒店和餐厅里的服务机器人等等。MC君在这篇文章中会谈谈聊天机器人的一个非常重要的技术——语音识别，希望能用最浅显的语言解析语音识别的基本原理。

一、语音识别

       语音识别，其实可以理解为说话的逆过程，我们平常说话是怎么说的？脑子里先想好一段内容，然后通过声音表达出来，而语音识别就刚好相反，计算机通过分析一段声音，来推测这段声音的内容是什么。最基本的语音识别是孤立词识别，也就是每次只能识别一个词，我们接下来通过一个简单的例子来说一下孤立词识别的原理。

       假如我现在要做一台校园导航机器人，其中一个功能是要识别用户说出的地名，如教学楼、饭堂、音乐厅、体育馆等，这些地名就是一个个孤立词，我们需要设计一个算法来让计算机来识别这些孤立词的语音，怎么做呢？我们知道声音其实是一种波，在信息学里面声音就是信号，是可以用具体的数字表达的，如果按照时间顺序将语音分割成一小段一小段，那么一段语音就可以表示成一个信号串 。那么，孤立词的语音识别问题可以理解为：给定一个信号串，找出最可能与之匹配的孤立词 ，写成概率的形式即：

                                                                      

      那其实就是求每个孤立词  的条件概率，这个概率似乎比较难计算，我们不妨利用贝叶斯公式进行一下转换：

                                                                     

      上式中，和很明显都是已知的，所以问题的关键就是求，即给定一段信号，求出与孤立词  匹配的概率。那这个概率应该怎么求呢？这时候就要用到著名的隐马尔可夫模型(Hidden Markov Model)，简称HMM。

二、隐马尔可夫模型

       隐马尔可夫模型是关于序列的概率模型，前面所说的信号串在这个模型中有个名字，叫做观测序列，顾名思义，也就是可以直接观测到的序列。既然有可观测的序列，自然就有不可观测的序列，HMM定义：观测序列中，任意时刻的观测  对应着一个隐状态，这些隐状态合在一起就形成了状态序列，所以这个模型叫做“ 隐”马尔可夫模型。举个具体的例子，我们说出一个词如“教学楼”，就形成了一段语音，这段语音每一时刻的信号就是，而其对应的隐状态是观测不到的，它可以是“教学楼”这个词的音标：ji，ao，x，ue，l，ou，当然也可以是其他东西，其实我们也不需要知道这些隐状态具体是什么，只需要知道一点：任意时刻的观测  跟隐状态  是一一对应的。

       所以现在回到刚才那个问题，求。如果孤立词  对应的模型参数是，那么就可以写成，因为现在多了一个状态序列，所以我们得想办法将塞进里面，怎么办呢？这就需要用到边缘分布的概念，可以表达为以下式子：

                                 

      上面这条长串的式子看起来就很复杂，所以为了把问题简单化，马尔可夫同志提出了两个假设：     

     （1）任意时刻的观测只与该时刻的状态有关，与其他时刻的状态和观测无关（独立），即：

                                 

     （2）任意时刻的状态只与前一个时刻的状态有关，与其他时刻的状态和观测无关（独立），即：

                                              

       有了以上两个假设，我们就可以把那条长串的式子写成下面这个样子（具体的推导比较简单，就不再赘述了）：

                                                            →1式

       细心的朋友可能会发现，等式左边的模型参数  消失了，那是因为在等式右边的、、就是模型参数，所以可以直接把去掉。所以，现在问题就变成了求、、这三个参数，需要说明的是：和都是随机变量，而并非具体的数值！所以要求这三个参数，必须知道、所有可能取到的值，假设、都是离散型随机变量，那么我们可以设是隐状态一切可能取值的集合（共有个取值）；是观测一切可能取值的集合（共有个取值），即：

                                             

      我们先看，因为和的可能取值都有个，那么可以写成一个的矩阵，如下所示：

                                           

       矩阵称作状态转移矩阵，那么在某个时刻，矩阵中第行，第列的元素可表示为：

                                                                 

       同理，也可以写成一个矩阵，的可能取值有个，的可能取值有个，那么可用一个的矩阵来表示，如下所示：

                                           

       矩阵称作观测概率矩阵，那么在某个时刻，的第行，第列的元素可表示为，即：

                                                                   

       那现在就剩下了，它代表初始时刻状态的概率，那应该就是一个N维的向量，我们用来表示，称作初始状态概率向量：

                                               

       其中，。

       咱们现在回到原来的式子，对于某个具体的观测值序列，，我们把、和代入到1式，就可以得到某参数条件下，发生的概率为：

                  

        并称为HMM的三元素，以上所有式子中的其实就是指这三个参数，即：。所以，我们只需要求出，就可以知道所有观测序列发生的概率。但是，先别急着求，还有一个问题需要解决，有没有发现上面这条式子的计算量其实是很大的，有多大？！所以，我们得想办法减少计算量才行，这需要用到一个算法：前向—后向算法。

三、前向—后向算法

        设从初始时刻到时刻的观测序列为，时刻的隐状态的取值为，那么就有如下定义：该观测序列与隐状态同时发生的概率为前向概率，记为：。

        当，有  ；

        当，有  ；

        我希望和发生联系，所以我需要把  塞进  里面，这又要用到前面的一个小技巧：边缘分布，如下式所示：

                                                    

                                                              

                                                              

        所以，就可以形成一个递归，当，就有：

                                              

       我们现在回到上节的问题，求，其实可以写成关于的表达式：

                                                                    

       所以，我们可以捋一下总的计算量，每个都要计算次，那的计算量就是，然后又要计算次，所以总计算量是。这个计算量比之前的要小得多，原因在于每一次计算直接引用了前一时刻的结果，而不需要重头开始，这个原理就有点像以前写过的动态规划的思想。所以可以直接用前向概率的算法进行计算。

       既然有前向概率，那应该也有一个后向概率，具体定义为：  设从到时刻的观测序列为，时刻的隐状态的取值为，则该观测序列在隐状态条件下发生的概率为后向概率，记为：。我们同样可以用递归的方式去求，递归的顺序是从到1，与前向概率刚好相反，递归过程如下：

                                                                      

                                                                     

                                                                                             

                                                                        

                                                                    

      用后向概率的计算量跟前向概率是一样的，前向概率和后向概率对于HMM来说非常重要，都可以起到减少计算量作用。那么，现在有了比较快速的计算方法，就可以去求HMM的模型参数，但是在语音识别中，是无法确定状态序列的，所以我们只能通过观测序列去推算模型参数，这类方法在机器学习中称为无监督训练方法，常用的方法是Baum-Welch算法。

四、Baum-Welch算法

       Baum-Welch算法实际上就是把EM算法应用在HMM，因为HMM除了观测数据意外，还有隐状态的数据，所以非常适合用EM算法来求模型参数，我们先回顾一下EM算法的过程（具体的算法推导见《原理解析——EM算法》）。

       首先，我们要求解的问题是：观测数据和未观测数据组成完全数据，求模型参数。

       求解的方法：EM算法，总的来说就是分两步走，先求期望（E步），然后将期望极大化（M步）。

     （1）E步：完全数据的对数似然函数，关于在给定和第次迭代的参数条件下，对的条件概率分布的期望称为函数。这是我见到过最拗口的概念，但无所谓，其实就是求一个条件期望，知道公式就行，公式如下：

                                 

     （2）M步：第次迭代的参数，就是取极大值时对应的参数，公式如下：

                                                                  

        现在，我们回到Baum-Welch算法，只需要把上面的过程套进HMM里面，所以问题就变成了：观测序列和状态序列组成完全数据，求模型参数。所以，在Baum-Welch算法中， 函数就变成了：

                                       

       由于是常数，求极大值时可以忽略，所以函数可写成以下形式：

                                                       

       我们可以看回第二节中的最后一条式子，易知可以写成下式：

                                                             

       所以，函数就可以写成这样子：

                                     

                                                     

       函数分成了三项相加，这三项的表达式分别是：

                                                          

                                                          

                                                          

        到这里，E步算是完成了，接下来就可以执行M步了，也就是将函数取极大值，求出相应的参数。我们可以仔细看一下 函数的三个子项，只出现了参数，只出现了参数，只出现了参数，也就是说三个参数在三个子项中是相互独立的，所以对函数取极大值，只需要分别对三个子项求极大值，然后分别求出各自的参数即可，这其实是一种化整为零的思想。

        首先对求极大值，我们看一下的表达式，要对个隐状态进行求和，看起来相当复杂，但我们仔细想一想，是什么，，所以参数只与第一个时刻的隐状态有关，只有第一个求和是有效的，那相应的，就只能取第一个隐状态。因此，的最终表达式应该是这样子的：

                                                                      

        别忘了，还有一个约束条件，那就是：

                                                                                    

       那现在对求极大值应该简单多了吧，在约束条件下求极大值，那自然就会想到拉格朗日乘子法，构造一个拉格朗日函数：

                                              

      令函数的偏导等于0，就可以求出相应的。具体求解过程就不写了，有兴趣的读者可以参考李航《统计学习方法》，里面有Baum-Welch算法的详细求解过程，直接奉上参数的最终表达式，表示第次迭代中的，：

                                                     

         接下来，函数的第二和第三项也是如法炮制，用拉格朗日乘子法来求极大值，最终可以得到另外两个参数的迭代公式：

                                                          

                                                           

        我们看上面三个参数的迭代公式，事实上只跟两个式子有关：和 ，这两个式子很明显不能直接在当前的参数里面找到，那到底怎么求呢？这时候就要用到之前说过的前向概率和后向概率。

        对于，我们可以作这样的变形：

                                       

                                                                                    

                                                                    

                                                                    

         所以，就等于前向概率和后向概率的乘积，把上式代入的表达式，可得到：

                                                              

         至于，可作如下推导（为了看起来不乱，下面的推导忽略了参数和隐状态的取值）：

                                           

                                                         

                                                         

                                                         

                                                         

                                                         

         因此，我们可以用前向和后向概率将参数求出，所以现在就可以写出完整的HMM参数估计的过程：

       （1）输入：观测序列，选取初始参数；

       （2）利用Baum-Welch算法对参数进行递归，求出

       （3）当参数收敛时终止程序，最终得到模型参数。        

五、孤立词识别

       我们先复习梳理一下HMM的训练和预测过程：

       首先，模型训练：给定训练样本，即观测序列，然后通过Baum-Welch算法求得模型的参数，迭代过程要用到前向和后向概率求解。

       然后，概率预测：将要进行预测的序列代入模型，然后通过前向—后向算法求得。

       事实上，上面的的两个过程就是HMM的三大基本问题的其中两个，即：

       问题一：已知观测序列，估计模型参数。

       问题二：已知模型参数和观测序列，求。

       至于第三个问题，也称作解码问题：已知模型参数和观测序列，求令最大的状态序列。这个问题在MC君的文章——中文分词与维特比算法中有具体解释。

       既然已经知道了HMM的算法过程，那现在就可以将HMM应用到校园导航机器人项目的孤立词识别，大概的步骤如下：

     （1）巧妇难为无米之炊，要做模型训练首先得有训练样本，那应该怎么得到这些训练样本呢？假设校园里面有50个地名需要识别，那就可以找个学生，录下他们说这50个地名的语音，这样每个地名（孤立词）都有了个初始样本，但这些样本还不能直接拿来训练，需要作一些处理。对于某个地名（如“音乐厅”），它的语音样本分别为，其中第个语音可以用一串向量序列表示，为语音的帧数（长度），该序列中每一个向量可以理解为这段语音在相应帧的特征向量。为了减少计算量，要先对这个向量进行聚类（VQ算法），生成个聚类中心，也就是代表性的向量，码本向量集。所以每个语音样本中的向量都可以映射到集合中的其中一个码本向量，也就是说语音样本的取值从变成了，这便形成了新的训练样本集，我们用新的符号表示：，，这便是我们用作训练的观测序列集，是观测一切可能取值的集合。

     （2）得到训练样本后，就可以利用这个观测序列进行HMM的参数估计，得到各个地名的模型参数，这就要用到Baum-Welch算法。但需要注意的是，第四节中的Baum-Welch算法只是对单个观测序列进行参数估计，但现在有个观测序列，最终只能生成一个模型参数，所以要对第四节中的公式进行一下修正，也很简单，只需要在分子分母同时对个观测序列求和，即在前面加上一个求和符号，修正后的式子就变成了这样子：

                                                       

                                                       

                                                       

     （3）根据上面的迭代公式，就可以得到各个地名的模型参数，最后就可以根据这些参数进行孤立词的识别。找一个学生随便说一个地名（一定得是50个地名中的其中一个），形成一段新的语音，分别映射到50个地名的码本向量集，求得这50个地名对应的观测序列分别为，然后计算各地名对应的HMM参数下的预测概率，，这里可用前向—后向算法进行计算，其中概率最大值对应的地名即为预测结果。

        以上就是隐马尔可夫模型应用在孤立词识别的整个过程，本人水平有限，如果有读者发现上述的算法有错漏，欢迎在评论区留言赐教。

 

笔记内容来源：吴军《数学之美》3、5章；李航《统计学习方法》；视频资料：徐亦达机器学习：隐马尔可夫模型