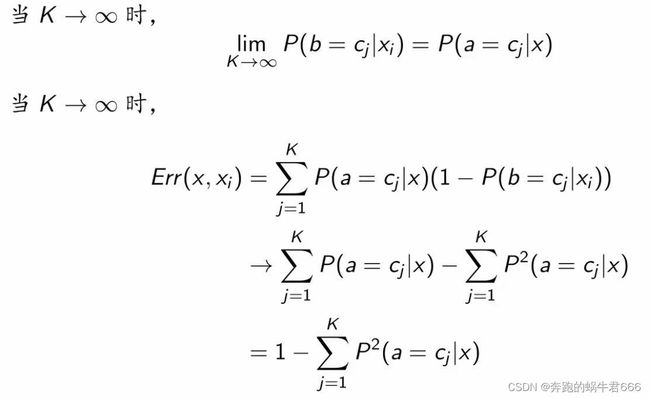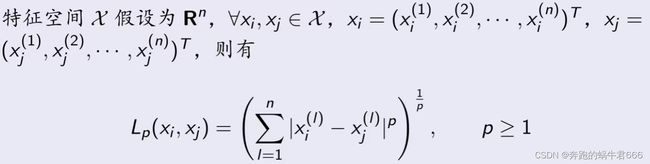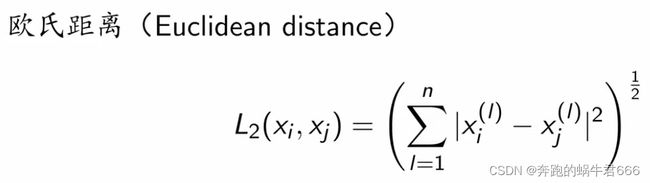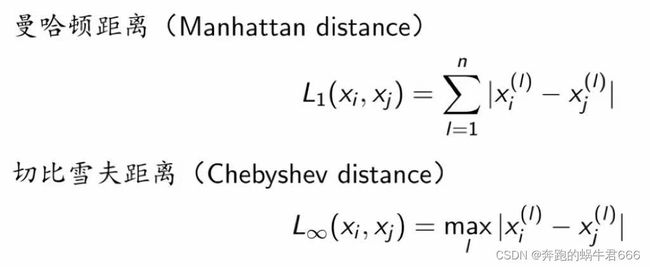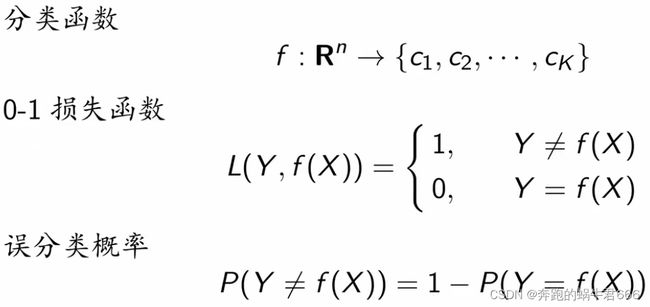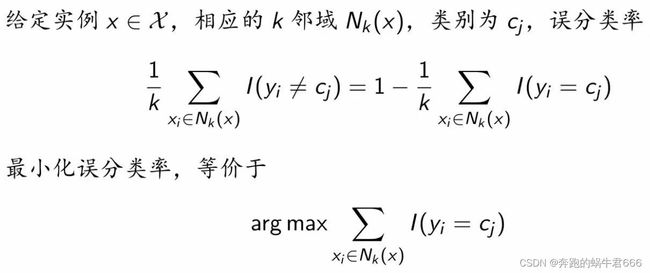统计学习方法 | K 近邻法

一.简介

1.直观理解

定义：是一种基本的分类与回归方法

主要思想：假定给定一个训练数据集，其中实例标签已定，当输入新的实例时，可以根据其最近的K个训练实例的标签，预测新实例对应的标注信息

分类问题：对新的实例，根据与之相邻的K个训练实例的类别，通过多数表决等方式进行预测

回归问题：对新的实例，根据与之相邻的K个训练实例的标签，通过均值计算进行预测

2.算法

3.误差率 

二.三要素

1.模型 

K近邻法不具有显性的学习过程，实际上利用训练数据集对特征向量空间进行划分，以其作为分类的模型

2.距离度量

3.K值的选择

较小的K值，学习的近似误差减小，但估计误差增大，敏感性增强，而且模型复杂，容易过拟合

较大的K值，减少学习的估计误差，但近似误差增大，而且模型简单

注：K的取值可通过交叉验证来选择，一般低于训练集样本量的平方根

4.分类决策规则

多数表决规则：由输入实例的K个邻近的训练实例中的多数类决定输入实例的类

三.构造 kd 树 

定义：kd 树是一种对 k 维空间中的实例点进行储存以便对其进行快速检索的树形数据结构

本质：二叉树，表示对 k 维空间的一个划分

构造过程：不断地用垂直于坐标轴的超平面将 k 维空间切分，形成 k 维超矩形区域

kd 树的每一个结点对应于一个 k 维超矩形区域

四.搜索 kd 树 

寻找 “当前最近点”：寻找最近邻的子结点作为目标点的 “当前最近点”

回溯：以目标点和 “当前最近点” 的距离沿树根部进行回溯和迭代

输入：以构造的 kd 树，目标点 x

输出：x 的最近邻

1.寻找 “当前最近点”

从根结点出发，递归访问 kd 树，找出包含 x 的叶结点

以此叶结点为 “当前最近点”

2.回溯

若该结点比 “当前最近点” 距离目标点更近，更新 “当前最近点”

当前最近点一定存在于该结点一个子结点对应的区域，检查子结点的父结点的另一子结点对应的区域是否有更近的点

3.当回退到根结点时，搜索结束，最后的 “当前最近点” 即为 x 的最近邻点

五.Python实现

class KNN:
    def __init__(self, X_train, y_train, n_neighbors=3, p=2):
        """
        parameter: n_neighbors 临近点个数
        parameter: p 距离度量
        """
        self.n = n_neighbors
        self.p = p
        self.X_train = X_train
        self.y_train = y_train

    def predict(self, X):
        # 取出n个点
        knn_list = []
        for i in range(self.n):
            dist = np.linalg.norm(X - self.X_train[i], ord=self.p)
            knn_list.append((dist, self.y_train[i]))

        for i in range(self.n, len(self.X_train)):
            max_index = knn_list.index(max(knn_list, key=lambda x: x[0]))
            dist = np.linalg.norm(X - self.X_train[i], ord=self.p)
            if knn_list[max_index][0] > dist:
                knn_list[max_index] = (dist, self.y_train[i])

        # 统计
        knn = [k[-1] for k in knn_list]
        count_pairs = Counter(knn)
#         max_count = sorted(count_pairs, key=lambda x: x)[-1]
        max_count = sorted(count_pairs.items(), key=lambda x: x[1])[-1][0]
        return max_count

    def score(self, X_test, y_test):
        right_count = 0
        n = 10
        for X, y in zip(X_test, y_test):
            label = self.predict(X)
            if label == y:
                right_count += 1
        return right_count / len(X_test)

clf = KNN(X_train, y_train)
clf.score(X_test, y_test)

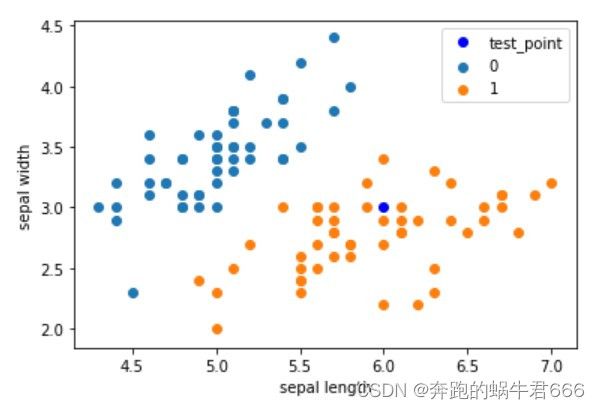
plt.scatter(df[:50]['sepal length'], df[:50]['sepal width'], label='0')
plt.scatter(df[50:100]['sepal length'], df[50:100]['sepal width'], label='1')
plt.plot(test_point[0], test_point[1], 'bo', label='test_point')
plt.xlabel('sepal length')
plt.ylabel('sepal width')
plt.legend()

kd 树 

# kd-tree每个结点中主要包含的数据结构如下
class KdNode(object):
    def __init__(self, dom_elt, split, left, right):
        self.dom_elt = dom_elt  # k维向量节点(k维空间中的一个样本点)
        self.split = split  # 整数（进行分割维度的序号）
        self.left = left  # 该结点分割超平面左子空间构成的kd-tree
        self.right = right  # 该结点分割超平面右子空间构成的kd-tree


class KdTree(object):
    def __init__(self, data):
        k = len(data[0])  # 数据维度

        def CreateNode(split, data_set):  # 按第split维划分数据集exset创建KdNode
            if not data_set:  # 数据集为空
                return None
            # key参数的值为一个函数，此函数只有一个参数且返回一个值用来进行比较
            # operator模块提供的itemgetter函数用于获取对象的哪些维的数据，参数为需要获取的数据在对象中的序号
            #data_set.sort(key=itemgetter(split)) # 按要进行分割的那一维数据排序
            data_set.sort(key=lambda x: x[split])
            split_pos = len(data_set) // 2  # //为Python中的整数除法
            median = data_set[split_pos]  # 中位数分割点
            split_next = (split + 1) % k  # cycle coordinates

            # 递归的创建kd树
            return KdNode(
                median,
                split,
                CreateNode(split_next, data_set[:split_pos]),  # 创建左子树
                CreateNode(split_next, data_set[split_pos + 1:]))  # 创建右子树

        self.root = CreateNode(0, data)  # 从第0维分量开始构建kd树,返回根节点


# KDTree的前序遍历
def preorder(root):
    print(root.dom_elt)
    if root.left:  # 节点不为空
        preorder(root.left)
    if root.right:
        preorder(root.right)