线性代数——特征值与特征向量
文章目录
- 定义与性质
-
- 几何学意义
- 性质
- 特征值计算
本篇笔记源于《程序员的数学之线性代数》
定义与性质
一般而言,对于方阵A,满足
A p = λ p p ≠ o \begin{array}{c} A \boldsymbol{p}=\lambda \boldsymbol{p} \\ \boldsymbol{p} \neq \boldsymbol{o} \end{array} Ap=λpp=o
的数 λ \lambda λ和向量p分别称为特征值和特征向量。
几何学意义
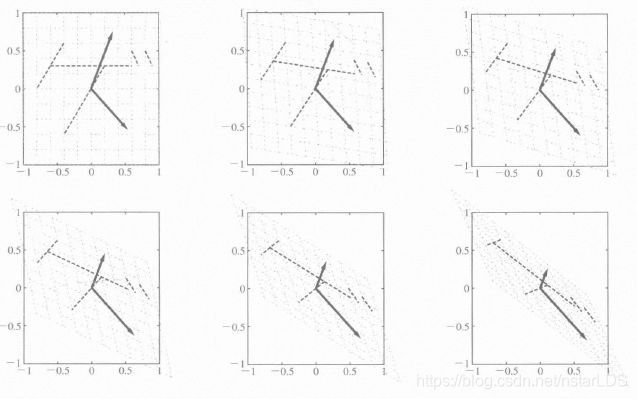
从几何学意义上讲,特征向量乘上A之后,除了长度会有伸缩变化,方向将不会发生改变。这里的长度变化倍率便是特征值。用动态图描述在2x2矩阵A的作用下,其两个特征向量的变化如图所示:
性质
令 λ \lambda λ, p \boldsymbol{p} p为方阵A的特征值和特征向量,则
- “A有0特征值”等价于“A是奇异矩阵”(0特征值就说明存在Ap=o,p不等于o,所以A的ker不为零,p至少有一维的信息映射到相同的结果,这一维在新空间中就无用了)
- “A没有0特征值”等价于“A可逆”(从行列式角度看A对角化后的行列式等于A的行列式,A行列式不为0于是A可逆)
- 对于 α ≠ 0 \alpha \neq 0 α=0, α p \alpha p αp也是A的特征向量,对应的特征值都是 λ \lambda λ
- 对于特征值 λ \lambda λ,若另有向量q也是其特征向量,那么p+q也是A的特征向量,对应特征值为 λ \lambda λ
- p是 α A \alpha A αA的特征向量,对应特征值为 α λ \alpha \lambda αλ
- p是 A + α I A+\alpha I A+αI的特征向量,对应特征值为 α + λ \alpha+\lambda α+λ
- p是 A k A^k Ak的特征向量,对应特征值为 λ k \lambda^k λk
- p是 A − 1 A^{-1} A−1的特征向量(前提是A逆存在),对应的特征值为 1 λ \frac{1}{\lambda} λ1
- S − 1 p S^{-1}p S−1p是 S − 1 A S S^{-1}AS S−1AS的特征向量,对应的特征值为 λ \lambda λ
- 对角矩阵 diag ( a 1 , ⋯ , a n ) \operatorname{diag}\left(a_{1}, \cdots, a_{n}\right) diag(a1,⋯,an)的特征值为 a 1 , ⋯ , a n a_{1}, \cdots, a_{n} a1,⋯,an,对应特征向量为 e 1 , ⋯ , e n e_{1}, \cdots, e_{n} e1,⋯,en
- 分块对角矩阵各个块矩阵的特征向量补0之后就是D的特征向量
最后一个性质具体描述如下,对
D = ( A O O O B O O O C ) D=\left(\begin{array}{lll} A & O & O \\ O & B & O \\ O & O & C \end{array}\right) D=⎝⎛AOOOBOOOC⎠⎞
p是A特征向量,q是B特征向量,r是c特征向量,则
( p o o ) , ( o q o ) , ( o o r ) \left(\begin{array}{l} p \\ o \\ o \end{array}\right), \quad\left(\begin{array}{l} o \\ q \\ o \end{array}\right), \quad\left(\begin{array}{l} o \\ o \\ r \end{array}\right) ⎝⎛poo⎠⎞,⎝⎛oqo⎠⎞,⎝⎛oor⎠⎞
是D的特征向量。
重要性质:设 λ 1 , ⋯ , λ k \lambda_{1}, \cdots, \lambda_{k} λ1,⋯,λk是n x n矩阵A的特征值, p 1 , ⋯ , p k \boldsymbol{p}_{1}, \cdots, \boldsymbol{p}_{k} p1,⋯,pk是对应的特征向量。若 λ 1 , ⋯ , λ k \lambda_{1}, \cdots, \lambda_{k} λ1,⋯,λk两两不同,则 p 1 , ⋯ , p k \boldsymbol{p}_{1}, \cdots, \boldsymbol{p}_{k} p1,⋯,pk两两线性无关。(不相等的特征值对应的特征向量线性无关)
这个性质的证明需要用反证法和归纳法,大致思路就是假设存在一组 ( c 1 , … , c k ) ≠ ( 0 , … , 0 ) (c_1, \dots , c_k) \neq (0, \dots,0) (c1,…,ck)=(0,…,0)使得 p 1 , ⋯ , p k \boldsymbol{p}_{1}, \cdots, \boldsymbol{p}_{k} p1,⋯,pk线性相关,则有
c 1 p 1 + ⋯ + c k p k = o c_{1} \boldsymbol{p}_{1}+\cdots+c_{k} \boldsymbol{p}_{k}=\boldsymbol{o} c1p1+⋯+ckpk=o
同时左乘A,有
c 1 A p 1 + ⋯ + c k A p k = o c_{1} A p_{1}+\cdots+c_{k} A p_{k}=o c1Ap1+⋯+ckApk=o
即
λ 1 c 1 p 1 + ⋯ + λ k c k p k = o \lambda_{1} c_{1} \boldsymbol{p}_{1}+\cdots+\lambda_{k} c_{k} \boldsymbol{p}_{k}=\boldsymbol{o} λ1c1p1+⋯+λkckpk=o
第一个式子乘 λ k \lambda_k λk倍减去上式,消元消掉 p k p_k pk,得
( λ 1 − λ k ) c 1 p 1 + ⋯ + ( λ k − 1 − λ k ) c k − 1 p k − 1 = o \left(\lambda_{1}-\lambda_{k}\right) c_{1} \boldsymbol{p}_{1}+\cdots+\left(\lambda_{k-1}-\lambda_{k}\right) c_{k-1} \boldsymbol{p}_{k-1}=\boldsymbol{o} (λ1−λk)c1p1+⋯+(λk−1−λk)ck−1pk−1=o
也就是
c 1 ′ p 1 + ⋯ + c k − 1 ′ p k − 1 = o c_{1}^{\prime} p_{1}+\cdots+c_{k-1}^{\prime} p_{k-1}=o c1′p1+⋯+ck−1′pk−1=o
因为特征值两两不同,原始的c不全为0,所以这里的c’也不全为0,所以就得到了和原式条件一模一样的少一个变量的等式。
循环往复以此类推。。。
最后得到
c 1 ′ ′ ′ p 1 = o c 1 ′ ′ ′ ≠ 0 \begin{aligned} c_{1}^{\prime \prime \prime} \boldsymbol{p}_{1} &=\boldsymbol{o} \\ c_{1}^{\prime \prime \prime} & \neq 0 \end{aligned} c1′′′p1c1′′′=o=0
那只能p为o了,但是前提是p是特征向量,所以矛盾。所以 p 1 , ⋯ , p k \boldsymbol{p}_{1}, \cdots, \boldsymbol{p}_{k} p1,⋯,pk只能线性无关了。
特征值计算
计算特征值就需要用到特征方程,其实特征方程并不是新东西,很简单,给定义式移项就能得到
( λ I − A ) p = o (\lambda I-A) \boldsymbol{p}=o (λI−A)p=o
这就说明 ( λ I − A ) (\lambda I-A) (λI−A)是个奇异阵,其行列式必为0。这就建立了等式了。我们把
ϕ A ( λ ) ≡ det ( λ I − A ) \phi_{A}(\lambda) \equiv \operatorname{det}(\lambda I-A) ϕA(λ)≡det(λI−A)
称为特征多项式,而 ϕ A ( λ ) = 0 \phi_{A}(\lambda)=0 ϕA(λ)=0就称为特征方程。通过解特征方程,就能得出特征值了。这里的特征值也会解得复数,也有其几何意义,但是在此就不展开讨论了。
笔记到这里可能有一个疑问,相同的特征值会不会造成什么问题?答案是有可能造成一些问题,比如n维矩阵,如果有相同的特征值,运气不好的话线性无关的特征向量可能最多只能得到小于n个。关于这个现象在后续的笔记中将继续详细讨论。