智能优化算法:风驱动优化算法-附代码
智能优化算法:风驱动优化算法-附代码
文章目录
- 智能优化算法:风驱动优化算法-附代码
-
- 1.算法原理
-
- 1.1 参数的编码
- 1.2 适应度函数的选取
- 1.3 空气单元运动范围的确定
- 1.4 风驱动中风的抽象化及空气单元的更新
- 2.算法结果
- 3.参考文献
- 4.Matlab代码
- 5.Python代码
摘要: 风驱动优化(Wind Driven Optimization,WDO)算法是由Bayraktar Z 等人在 2010年提出的一种基于群体的全局优化算法 。该算法基于对简化的空气质点受力运动模型的模拟,其核心是研究空气质点在大气中的受力运动情况,结合牛顿第二定律及理想气体状态方程,推导出空气质点在每次迭代中的速度和位置更新方程。相比于其他智能优化算法,该算法更新方程具有一定的物理意义,能够保证空气质点的全局“探索”能力与局部“开发”能力的平衡。
1.算法原理
风驱动优化算法(WDO)的启发来自于大气的流动,也就是风的运动可以自动补偿大气压力的不平衡 。根据牛顿第二定律来描述一个极小空气单元的运动规律,以空气单元的最终流动位置为候选解,从而完成对问题的最优求解,该算法概念明确、清晰、易于理解,是自然启发式算法研究领域的一种新型全局优化算法。
1.1 参数的编码
设空气 P 中的空气单元个体数为 S ,每个个体的位置矢量的维数 为D 。该种群可以用一个 SxD的矩阵来表示:
P ( S , D ) = [ K p 1 K i 1 K d 1 K p 2 K i 2 K d 2 . . . . . . . . . K p s K i s K d s ] (1) P(S,D)=\left[\begin{matrix} K_p^1&K_i^1&K_d^1\\ K_p^2&K_i^2&K_d^2\\ ...&...&... \\ K_p^s&K_i^s&K_d^s\\ \end{matrix}\right] \tag{1} P(S,D)=⎣⎢⎢⎡Kp1Kp2...KpsKi1Ki2...KisKd1Kd2...Kds⎦⎥⎥⎤(1)
考虑到空气受地域的影响,可以由用户根据具体工程背景决定各个参数的取值范围,初始空气单元在相应的取值范围内随机产生。
1.2 适应度函数的选取
WDO算法在搜索进化过程中不仅用压力函数值来评价个体或解的优劣,并作为以后空气单元位置更新的依据,使得初始解逐步向最优解迭代。压力函数是空气单元优化算法与控制系统结合的纽带,指导着算法按控制目标要求不断迭代。
1.3 空气单元运动范围的确定
对于每一维度,风驱动优化算法只允许空气单元在设定的范围内运动。在任何维度中,如果空气单元试图冲出这些界限,那么这些特殊的维度位置就被设置为界限值。因此空气单元位置约束如下:
u n e w = { u m a x , u > u m a x u m i n , u < u m i n (2) u_{new}=\begin{cases} u_{max},u>u_{max}\\ u_{min},u
1.4 风驱动中风的抽象化及空气单元的更新
不同地区的不同温度导致空气密度和大气压不同,不同大气压使空气由气压高的地区流向气压低的地区。导致这种流动原因是气压梯度 Δ P \Delta P ΔP ,它可以通过距离的变化计算出来,在直角坐标系中表示如下:
Δ P = ( δ P δ x , δ P δ y , δ P δ z ) (3) \Delta P = (\frac{\delta P}{\delta x},\frac{\delta P}{\delta y},\frac{\delta P}{\delta z})\tag{3} ΔP=(δxδP,δyδP,δzδP)(3)
特别地,风从高压地区向低压地区做匀速运动 。为了表明气压梯度降低的方向,式(4)中添加了负号。考虑到空气有限的质量和体积 δ V \delta V δV,压强梯度力 F P G F_{PG} FPG表示如下:
F P G = − Δ P δ V (4) F_{PG}= -\Delta P\delta V \tag{4} FPG=−ΔPδV(4)
在风的抽象化中,假设大气是均匀的,并符合流体静力学平衡。由直角坐标系中流体动力学方程,空气的水平流动强于垂直流动,即认为风只有水平运动,即风产生原因全部来自水平压力的变化。
根据牛顿第二运动定律,作用在空气单元上的合力方向下的加速度 a 计算如下:
ρ a = ∑ F i (5) \rho a=\sum F_i \tag{5} ρa=∑Fi(5)
其中 ρ ρ ρ 表示极小空气单元的密度, F i F_i Fi 代表作用在空气单元上的力。为了把空气压力和空气密度和温度联系起来,可以利用如下气体定律:
P = ρ R T (6) P = \rho RT \tag{6} P=ρRT(6)
其中 P P P 表示压力, R R R 代表通用气体常量, T T T 代表温度。
压强梯度力是使空气单元流动的基本力,然而存在阻止空气单元流动的摩擦力 F F F_F FF,由于作用在大气上的摩擦力非常复杂,在这里简化如下:
F F = − ρ a u (7) F_F=-\rho au \tag{7} FF=−ρau(7)
其中 α α α 为摩擦系数, u u u 为风的速度矢量。
在实际三维空间里,重力 F G F_G FG是一个垂直于地球表面的力。然而,如果把地球中心当做直角坐标系的原点,重力可简化为:
F G = ρ δ V g (8) F_G=\rho \delta Vg \tag{8} FG=ρδVg(8)
地球的旋转造成参考坐标系旋转,从而增加了科氏力。科氏力使风的方向从它的出发点发生偏转,偏转的角度和地球的旋转、对流层的纬度以及空气单元的流动速度有直接关系。科氏力的定义如下:
F c = − 2 Ω ∗ u (9) F_c = -2\Omega*u\tag{9} Fc=−2Ω∗u(9)
其中 Ω 表示地球的自转。
把式(4)、式(7)~式(9)代入方程(5)右边,得
ρ Δ u Δ t = ( ρ δ V g ) + ( − Δ P δ V ) + ( − ρ a u ) + ( − 2 Ω u ) (10) \rho \frac{\Delta u}{\Delta t}=(\rho \delta Vg)+(-\Delta P\delta V)+(-\rho au) + (-2\Omega u)\tag{10} ρΔtΔu=(ρδVg)+(−ΔPδV)+(−ρau)+(−2Ωu)(10)
式(10)中,设时间差 Δ t = 1 \Delta t= 1 Δt=1 , δ V = 1 δV = 1 δV=1 ,则可化简式(10)为:
ρ Δ u = ( ρ g ) + ( − Δ P ) + ( − ρ a u ) + ( − 2 Ω u ) (11) \rho \Delta u = (\rho g)+(-\Delta P)+(-\rho au) + (-2\Omega u) \tag{11} ρΔu=(ρg)+(−ΔP)+(−ρau)+(−2Ωu)(11)
利用式(6),可以把密度 ρ ρ ρ写成压力的形式,并将温度和普通气体常数代入式(11)得:
P c u r R T Δ u = ( p c u r R T g ) − Δ P − p c u r R T a u + ( − 2 Ω ∗ u ) (12) \frac{P_{cur}}{RT}\Delta u=(\frac{p_{cur}}{RT}g) - \Delta P - \frac{p_{cur}}{RT}au+(-2\Omega *u)\tag{12} RTPcurΔu=(RTpcurg)−ΔP−RTpcurau+(−2Ω∗u)(12)
其中 p c u r p_{cur} pcur 代表在当前压力值。式(12)两边同时除以$p_{cur} /RT $得:
Δ u = g + ( − Δ P R T p c u r ) − a u + ( − 2 Ω ∗ u R T p c u r ) (13) \Delta u = g+(-\Delta P\frac{RT}{p_{cur}})-au+(\frac{-2\Omega *uRT}{p_{cur}})\tag{13} Δu=g+(−ΔPpcurRT)−au+(pcur−2Ω∗uRT)(13)
其中, Δ u = u n e w − u c u r \Delta u= u_{new} - u_{cur} Δu=unew−ucur ,其中 u c u r u_{cur} ucur 当前迭代的速度, u n e w u_{new} unew表示下一个迭代的速度。用代入式(13)得:
u n e w = ( 1 − a ) u c u r + g + ( − Δ P ∗ R T / P c u r ) + ( − 2 Ω ∗ u R T / p c u r ) (14) u_{new}=(1-a)u_{cur}+g+(-\Delta P*RT/P_{cur})+(-2\Omega *uRT/p_{cur})\tag{14} unew=(1−a)ucur+g+(−ΔP∗RT/Pcur)+(−2Ω∗uRT/pcur)(14)
其中,矢量 g g g 可以表示为: g = ∣ g ∣ ( 0 − x c u r ) g= |g|(0- x_{cur} ) g=∣g∣(0−xcur)。压强梯度压力 ( Δ P \Delta P ΔP) 是使空气单元从当前位置移动到最优压力位置的一个力。因此有 Δ P \Delta P ΔP 的大小为空气单元当前的压力 p c u r p_{cur} pcur 与目前发现的最佳压力 p o p t p_{opt} popt 的差,压强梯度压力的方向由当前位置 x c u r x_{cur} xcur 指向最优位置 x o p t x_{opt} xopt 。 Δ P \Delta P ΔP 可以简单表示为:
Δ P = ∣ p n e w − p o p t ∣ ( x c u r − x o p t ) (15) \Delta P = |p_{new}-p_{opt}|(x_{cur}-x_{opt})\tag{15} ΔP=∣pnew−popt∣(xcur−xopt)(15)
由此可得:
u n e w = ( 1 − a ) u c u r + g x c u r + ( − ∣ p n e w − p o p t ∣ ( x c u r − x o p t ) ∗ R T / P c u r ) + ( − 2 Ω ∗ u R T / p c u r ) (16) u_{new}=(1-a)u_{cur}+gx_{cur}+(-|p_{new}-p_{opt}|(x_{cur}-x_{opt})*RT/P_{cur})+(-2\Omega *uRT/p_{cur})\tag{16} unew=(1−a)ucur+gxcur+(−∣pnew−popt∣(xcur−xopt)∗RT/Pcur)+(−2Ω∗uRT/pcur)(16)
在式(16)中,科氏力表示为地球自转速度和空气单元加速度的矢量积。科氏力的影响可以简单地表示为:由其他相同空气单元随机选择速度 u c u r o t h e r d i m u_{cur}^{otherdim} ucurotherdim来代替,设 c = − 2 ∣ Ω ∣ R T c= -2|Ω|RT c=−2∣Ω∣RT ,把简化的科氏力代入(16),得:
u n e w = ( 1 − a ) u c u r + g x c u r + ( − ∣ p n e w − p o p t ∣ ( x c u r − x o p t ) ∗ R T / P c u r ) + ( c u c u r o t h e r d i m / p c u r ) (17) u_{new}=(1-a)u_{cur}+gx_{cur}+(-|p_{new}-p_{opt}|(x_{cur}-x_{opt})*RT/P_{cur})+(cu_{cur}^{otherdim}/p_{cur})\tag{17} unew=(1−a)ucur+gxcur+(−∣pnew−popt∣(xcur−xopt)∗RT/Pcur)+(cucurotherdim/pcur)(17)
为了防止压力值过高,风速可能会变得非常大,风驱动优化算法的性能也会降低。可以利用排序法把所有空气单元以压力值按降序排序,这样可以把方程(17)写成:
u n e w = ( 1 − a ) u c u r + g x c u r + ( ( x c u r − x o p t ) ∗ R T ∣ 1 / i − 1 ∣ ) + ( c u c u r o t h e r d i m / i ) (18) u_{new}=(1-a)u_{cur}+gx_{cur}+((x_{cur}-x_{opt})*RT|1/i - 1|)+(cu_{cur}^{otherdim}/i)\tag{18} unew=(1−a)ucur+gxcur+((xcur−xopt)∗RT∣1/i−1∣)+(cucurotherdim/i)(18)
其中 i 代表所有空气单元的排名。由此得到位置更新方程如下:
x n e w = x c u r + ( u n e w Δ t ) (19) x_{new}=x_{cur}+(u_{new}\Delta t)\tag{19} xnew=xcur+(unewΔt)(19)
其中 x c u r x_{cur} xcur 是搜索空间中空气单元的当前位置, x n e w x_{new} xnew 是下一个循环状态新的位置。在搜索空间中,所有的空气单元在随机位置以随机速度移动。利用公式(18)和(19),每一个空气单元的速度和位置在每次迭代中都会得到调整,如同空气单元向最优位置移动一样,因此,最后的循环是最优的解决办法。
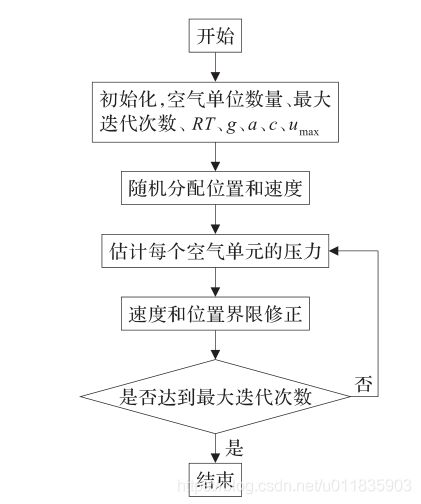
风驱动优化算法的流程如图1所示:
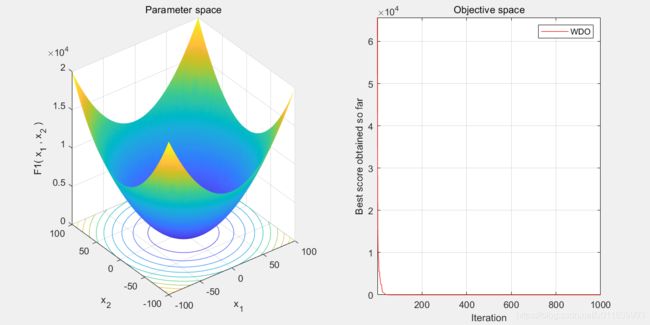
2.算法结果
3.参考文献
[1] Bayraktar Z,Komurcu M,Bossard J A,et al.The wind driven optimization technique and its application in elec-
tromagnetics[J].IEEE Transactions on Antennas and Propa-gation,2013,61(5):2745-2755.
[2] 陈彬彬,曹中清,余胜威.基于风驱动优化算法WDO的PID参数优化[J].计算机工程与应用,2016,52(14):250-253+260.
4.Matlab代码
风驱动优化算法
算法相关应用
| 名称 | 说明或者参考文献 |
|---|---|
| 基于风驱动算法优化的SVM数据分类 | https://blog.csdn.net/u011835903/article/details/110523352(原理一样,只是优化算法用风驱动算法) |
5.Python代码
个人资料介绍