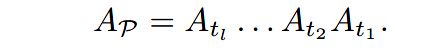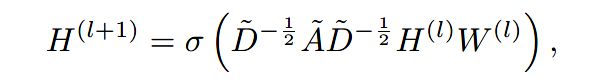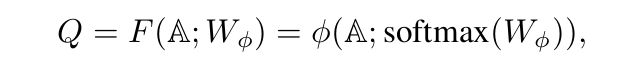【论文解读 NIPS 2019 | GTNs】Graph Transformer Networks

论文题目：Graph Transformer Networks

论文来源：NIPS 2019

论文链接：https://arxiv.org/abs/1911.06455

代码链接：https://github.com/seongjunyun/Graph_Transformer_Networks

---

---

1 摘要

本文解决的是HIN中的节点嵌入学习问题。

现有的GNN大多在固定且同质的图上进行节点的表示学习。

本文提出了一种能够生成新的图数据结构的图变换网络（Graph Transformer Networks, GTNs），它包括识别原始图数据中未连接节点之间的有用连接，同时以端到端方式学习新图数据中有效的节点表示。

图变换层（Graph Transformer layer）是GTNs中的核心层，它可以选择出边类型和组合关系，以生成有用的多跳连接，即元路径。

实验表明GTNs基于无先验知识的数据和任务，通过在新图上进行卷积，可以学习出有效的节点表示。

在三个基线的节点分类任务上超越state-of-the-art，并且对比的这些方法都需要预先定义元路径。

2 引言

GNN的局限性：

（1）大多数GNN是能在固定且同质的图上进行运算。如果图上有噪声，缺失连边或者有错误的连边，就会导致与图上错误的邻居进行无效的卷积。

（2）大多数GNN忽略了节点/边的类型，使用人为设定的元路径将异质图转化成同质图，不能充分利用图中的信息。并且选择的元路径将会在很大程度上影响下游任务的准确率。

这种方式是**两步走（two-stage）**的方法：

1. 针对特定任务/数据集，人为设计元路径；
2. 根据元路径将异质图转化为同质图，在其上面应用GNN。

---

作者提出：

作者提出GTN，可以看成是空间转换网络（STN）向图数据的扩展。具体表现为将HIN转换成由元路径定义的新的图结构，就可以直接在新图上进行节点的表示学习，是**端到端（end-to-end）**的学习模式。

---

将HIN转换为元路径定义的新的图结构带来的挑战：

1. 元路径的长度不固定，元路径中边的类型也是任意的；
2. 能应用于有向图的GNN相对较少。

---

基于上述挑战，作者提出：

提出模型生成新的图结构，该模型基于HIN中由所选边类型相连的复合关系，并在给定问题下的图结构上进行卷积操作以学习到节点表示。

3 模型

GTNs框架的目的是为原始图生成新的图结构，并在新图上进行节点表示学习。

与大多数在给定图上进行CNN的方法不同，GTNs使用多个候选的邻接矩阵生成新的图结构，以实现更有效的图卷积，学习到表示能力更强的节点嵌入表示。

3.1 定义

3.1.1 异质图

1. 异质图$G=(V,E)$，$V$是节点集合，$E$是边集合；
2. $T^v,T^e$分别是节点类型集合和边类型集合；
3. 异质图可表示成一组邻接矩阵$\{A_k{\}}_{k=1}^K,K=|T^e|$。$A_k\in R^{N\times N}$是邻接矩阵，若节点$j$到$i$之间有第$k$中类型的边相连，则$A_k[i,j]\ne 0$。也可以写成张量的形式：$A\in R^{N\times N\times K}$；
4. 节点的特征矩阵为$X\in R^{N\times D}$.

3.1.2 元路径

元路径$P$的邻接矩阵表示成元路径中不同类型的边对应的邻接矩阵的乘积：

3.1.3 GCN

其中$\tilde{A}=A+I\in R^{N\times N}$，$\tilde{D}$是$\tilde{A}$的度矩阵，$W^{(l)}\in R^{d\times d}$是可训练的参数矩阵。

对于有向图则将${\tilde{D}}^{-\frac{1}{2}}\tilde{A}{\tilde{D}}^{-\frac{1}{2}}$换成${\tilde{D}}^{-1}\tilde{A}$

由上式可以看出，卷积操作是由给定的图结构决定的，且只有针对节点的线性转换参数$H^{(l)}{W}^{(l)}$是可学习的。因此，卷积层可以被解释成固定卷积的组合，在图上经过节点级别的线性变换后再通过一个激活函数。

3.2 元路径的生成

先前的工作都是人工定义元路径，然后在其基础上进行GNN。本文提出的GTNs为给定的数据和任务学习到元路径，然后在学习到的元路径图（meta-path graphs）上进行图卷积。

---

3.2.1 GT层

元路径图的生成过程如上图的图变换层（GT）层所示，分为两步：

• 首先，GT层从候选的邻接矩阵$A$（每一片都代表一种边类型）中选择出两个图结构$Q_1,Q_2$；

• 然后，将其组合得到新的图结构（例如 将两个邻接矩阵相乘，$Q_1{Q}_2$）。

接下来逐步分析一下

（1）邻接矩阵$Q$是通过下式的计算选择出来的：

其中$\varphi$表示卷积操作，$W_{\varphi }\in R^{1\times 1\times K}$是$\varphi$的参数。其实$Q$的选择类似使用了注意力机制。

以图1为例，输入的原始图的邻接矩阵$\mathbb{A}\in R^{N\times N\times K}$（$K=4$）一共有4片，每一片对应着一种类型的边的邻接矩阵，即原始图中一共有4种类型的边。

使用$softmax$函数归一化后的$W_{\varphi }\in R^{1\times 1\times K}$就是$1\times 1$卷积层的参数。卷积后得到的邻接矩阵，可以看成是在原邻接矩阵上应用了注意力机制，为各个片分配了不同的注意力系数作为每片的权重，加权求和得到新的邻接矩阵$Q$。

矩阵$Q$的每一片$Q_i$可以表示成：${\sum }_{t_l\in T^e}{\alpha }_{t_l}^{(l)}{A}_{t_l}$，其中${\alpha }_{t_l}^{(l)}$就是$1\times 1$卷积层中的参数，$l$表示位于第几层。

图1中的$Q_1,Q_2$分别是$Q$的两个片，也就是说经过$1\times 1$卷积操作后，输入从$\mathbb{A}\in R^{N\times N\times 4}$转换成了$Q\in R^{N\times N\times 2}$。

（2）将选择出的邻接矩阵组合得到新的图结构：

采用矩阵相乘的方式，如图1所示：$A^{(l)}=Q_1{Q}_2$。为了数值稳定，使用度矩阵进行归一化：$A^{(l)}=D^{-1}{Q}_1{Q}_2$。

长度为$l$的元路径对应的邻接矩阵$A_P$计算为：

其中$T^e$表示边类型的集合，${\alpha }_{t_l}^{(l)}$为对类型为$t_l$的边在第$l$层中的权重。

---

3.2.2 多层堆叠

由3.2.1可知，当$\alpha$不是one-hot向量时，$A_P$就可以看成是所有长度为$l$的元路径的邻接矩阵的加权和。

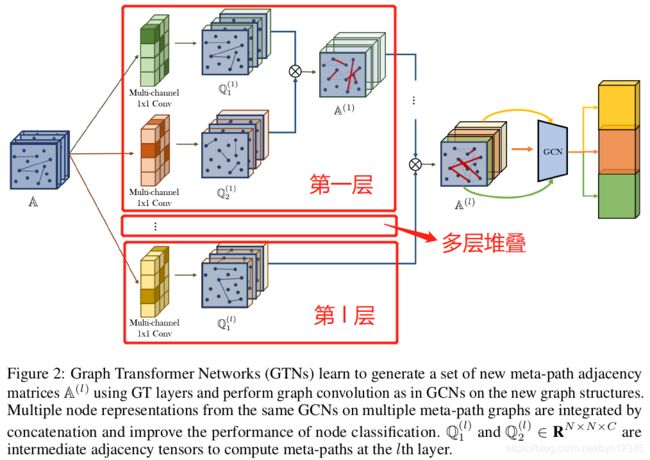
因此堆叠$l$层GT层就可以学习到任意的长度为$l$的元路径图结构，如图2所示。

假定卷积的输出通道为$1$，第$l$层GT层为新的元路径图生成的邻接矩阵$A^{(l)}$计算如下：

将迭代展开后可得：

其中$T^e$表示边类型的集合，${\alpha }_{t_l}^{(l)}$为对类型为$t_l$的边在第$l$层中的权重。因此，$A^{(l)}$可以看成是对所有长度为$1$~$l$的元路径的加权和。元路径$t_l,t_{l-1},...,t_0$的贡献度计算为${\prod }_{i=0}^l{\alpha }_{t_i}^{(i)}$。

---

注意：

生成的元路径长度等于GT层的层数，所以堆叠的层数越多，则生成的元路径越长，而且堆叠多层后原始图中的连边可能不存在了。然而，有的时候短的元路径也很重要。

为了学习到包含原始图中连边的长的元路径和短的元路径，在$\mathbb{A}$中加入单位矩阵$I$，例如$A_0=I$。这样，当有$l$层GT层时，就可以学习到长度为$1$~$l$的元路径。

3.3 Graph Transformer Networks

为了同时生成多种类型的元路径，将图1中卷积的输出通道设置为$C$，如图2所示。随后GT层产生一组元路径，图1中的$Q_1,Q_2$成为图2中的张量${\mathbb{Q}}_1^{(l)},{\mathbb{Q}}_2^{(l)}\in R^{N\times N\times C}$。${\mathbb{Q}}_1^{(l)},{\mathbb{Q}}_2^{(l)}$是为了计算元路径，得到的第$l$层的邻接张量的中间值。

通过多个不同的图结构学习到不同的节点表示是很有帮助的。

$l$表示生成的元路径的最大长度，$C$表示生成几条元路径。

在$l$个GT层堆叠后，将GCN应用于元路径张量${\mathbb{A}}^l\in R^{N\times N\times C}$的每个通道，并将多个节点的向量表示拼接起来：

其中，$||$是连接操作，$C$是通道数，${\hat{A}}_i^{(l)}=A_i^{(l)}+i$是${\mathbb{A}}^{(l)}$的第$i$个通道的邻接矩阵，${\hat{D}}_i$是${\hat{A}}_i^{(l)}$的度矩阵，$W\in R^{d\times d}$是$1\times 1$卷积中需要训练的权重矩阵，$X\in R^{N\times d}$是输入的特征矩阵。

$Z$包含节点在$C$个元路径图中的表示，元路径的长度最长为$l$。

将$Z$用于有监督的节点分类任务，构造优化目标。分类器的结构为：$Z$输入到2层的稠密层，然后再过一层softmax。损失函数是交叉熵函数。

整个模型架构可以看成是：在由GT层学习到的多个元路径图（meta-path graphs）上进行GCN。

4 实验

实验并分析，回答如下的几个问题：

1. GTN生成的新的图结构对节点的表示学习有效吗？
2. GTN是否能根据数据集自适应地生成变长的元路径？
3. 如何从GTN生成的邻接矩阵来解释每个元路径的重要性？

数据集：

实验任务：节点分类

对比方法：

（1）传统的网络嵌入学习方法

• DeepWalk
• metapath2vec

（2）基于GCN的方法

• GCN
• GAT
• HAN

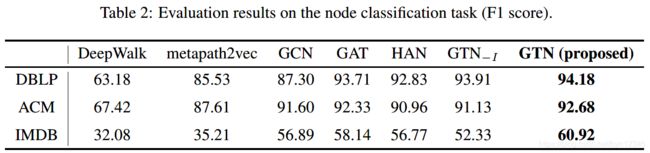
实验结果：

（1）节点分类实验结果

其中$GT{N}_{-I}$表示候选邻接矩阵$\mathbb{A}$没有包含单位矩阵。实验可以看出，使用3层的GT层，只能为IMDB数据集生成长度为4的元路径，效果很不好，因为IMDB中长度更短的元路径更合适。

（2）解释元路径的重要性

由3.2.2可知，元路径$t_l,t_{l-1},...,t_0$的注意力分数计算为${\prod }_{i=0}^l{\alpha }_{t_i}^{(i)}$，代表了在预测任务中这条元路径的重要性。表3就展示了GTNs学习到的注意力得分最高的元路径，以及预定义的元路径，证明了GTNs可以学习到针对特定任务的比较重要的元路径。

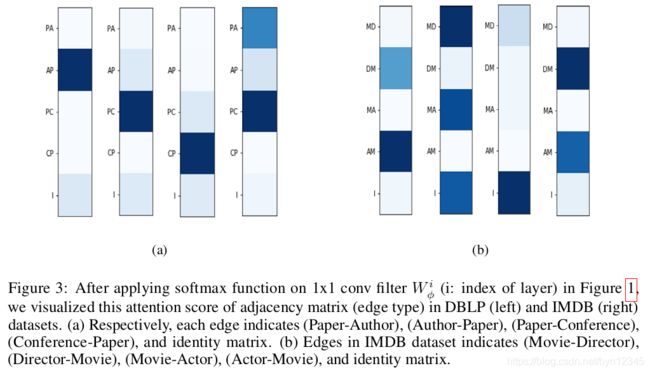
（3）GTNs根据数据集自适应地学习到变长的元路径

图3展示了每层GT层不同邻接矩阵（不同类型的边）的注意力分数。IMDB和DBLP相比，单位矩阵的注意力分数较高，说明GTNs能学习到比GT层数少的较短的元路径。

5 总结

这篇文章很有开创性。

本文提出图转换网络（GTNs）用于HIN上的节点表示学习。

将HIN转换为多个由元路径定义的新图，并且元路径中的边类型任意，长度是从$1$~$l$的任意长度（$l$为GT层层数）。然后在学习到的元路径图上通过卷积操作，进行节点表示的学习。

GTNs的一大特点是，不需要预先定义元路径，也就是不需要专家的先验知识。GTNs可以为给定的数据集自适应地学习到合适长度的元路径，元路径的重要性体现为注意力分数。

未来的研究方向：

（1）本文在GT层之后使用的数GCN方法，后续可以研究使用其他的GNN方法；

（2）本文只在节点分类任务上体现出了很好的效果，后续可以研究在其他任务上的效果，例如链接预测、图分类等。