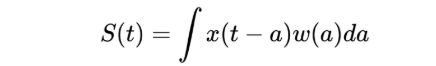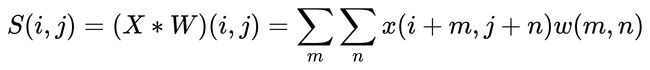介紹卷积神经网络（CNN）模型结构

介紹卷积神经网络（CNN）模型

1 CNN的基本结构

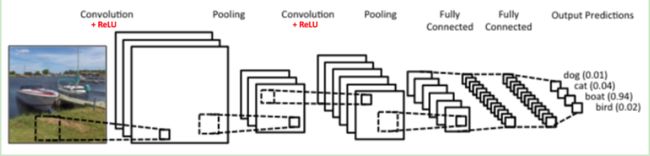
​ 一个常见的CNN例子如下图：

这是一个图像识别的CNN模型。最左边的船就是我们的输入层，计算机可理解为若干个矩阵。

接下来就是卷积层（Convolution Layer），这是CNN特有的。卷积层所使用的激活函数是ReLU。

ReLU(x)=max(0,x)。在卷积层后面是池化层（Pooling layer），这个也是CNN特有的，池化层没有激活函数。

上图中卷积层+池化层出现了两次，其实这些次数可以根据模型的需要来变换，也可灵活使用卷积层+卷积层，或者卷积层+卷积层+池化层的组合，常见的CNN都是若干卷积层+池化层的组合。

若干个卷积层+池化层后面是全连接层（Fully Connected Layer，简称FC）,全连接层其实就是DNN结构。接下来我们主要介绍卷积层和池化层。

2 卷积介绍

在微积分中卷积的表达式为：

离散形式是：

这个式子用矩阵表示为：

其中*表示卷积。

若是二维的卷积，则可表示为：

在CNN中，虽然也说成卷积，但此卷积和严格意义数学中的卷积定义稍有不同，比如对二维的卷积，在CNN中定义为：

其中，W是卷积核，X是输入。如果X是一个二维输入的矩阵，而W也是一个二维的矩阵。若X是多维张量，则W也是一个多维张量。X和W的维数保持相同。

3 CNN中的卷积层介绍

将卷积公式 应用于CNN的卷积层，即对输入的图像的不同局部的矩阵和卷积核矩阵各个位置元素相乘再相加。

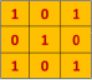
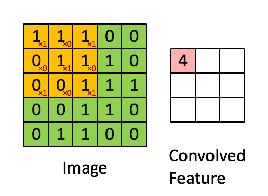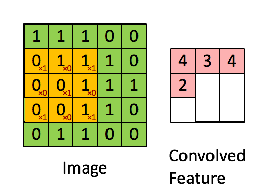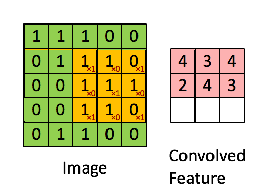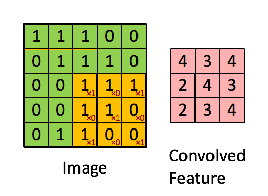
下图中，输入是一个二维的3×4矩阵，卷积核也是二维的，大小为2×2。假设卷积是一次移动一个像素进行卷积，首先对输入的左上角的2×2局部进行卷积，即采用卷积核对其进行元素相乘再相加，得到一个具体的数字。再向右将卷积核移动一个像素的大小，同样相乘再相加得到另一个数字。

将卷积核依次向右向下移动进行卷积后得到输出矩阵S的各个元素，由于卷积核在输入上能进行六次卷积运算，S矩阵最终是一个2×3的矩阵。

动态的卷积过程：

绿色的是输入为5×5大小的矩阵，卷积核为3×3大小的矩阵，卷积的步幅设为一个像素，如下图所示：

上述举例均是二维卷积。若输入时多维的，比如输入是三个矩阵时，又或者对应RGB的彩色图像时，该如何卷积呢？有个动态的例子展示输入为三维的卷积过程：
点击此处
例子中将输入原本时3个5×5的矩阵扩展成了3个7×7的矩阵（即在原本矩阵周边加了1的padding）。在本例中，使用了两个卷积核W0和W1，每个卷积核分别是3×3×3的张量，可理解为3×3是卷积核的大小，最后的3是卷积核的维数，此处维数须和输入矩阵维数相同。这个例子中，卷积运算的步幅为2，即就是每次卷积会移动2个像素的位置。

最终卷积的过程和二维矩阵类似，上面是矩阵的卷积，即两个矩阵对应位置的元素相乘后相加。此处是张量的卷积，即两个张量（卷积核）的3个子矩阵卷积后，再把卷积的结构相加后加上偏倚量b。

7×7×3的张量和3×3×3的卷积核张量W0卷积的结果是一个3×3的矩阵，由于此处用到了两个卷积核W0和W1,因此最后卷积的结果是两个3×3的矩阵，或者说卷积的结构是一个3×3×2的张量。

再简要复述上面过程，输入是7x7x3的张量，卷积核是两个3x3x3的张量。卷积步幅为2，最后得到了输出是3x3x2的张量。如果把上面的卷积过程用数学公式表达出来就是：

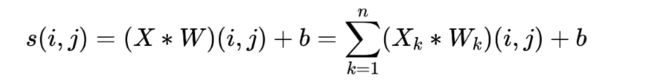
其中，n为输入矩阵的个数，或者可以说成张量的最后一维的维数。X_k代表第第k个输入矩阵。W_k代表卷积核的第k个子卷积核矩阵。s(i,j)即卷积核W对应的输出矩阵的对应位置的元素的值。

对于卷积后的输出，一般会通过ReLU激活函数，将输出的张量中的小于0的位置对应的元素值都变为0。

4 CNN中的池化层

池化层相比卷积层要简单一些，池化，即就是对输入张量的各个子矩阵进行压缩。假如是2×2的池化，那么就是将子矩阵的每2×2个元素变成一个元素，这样使输入矩阵的的维度就会减小。

若想将输入子矩阵的每n×n元素变成一个元素，那么就需要一个池化标准。常见的池化标准有两个：MAX和AVERAGE。即用对应区域的最大值或者平均值来作为池化后的元素值。

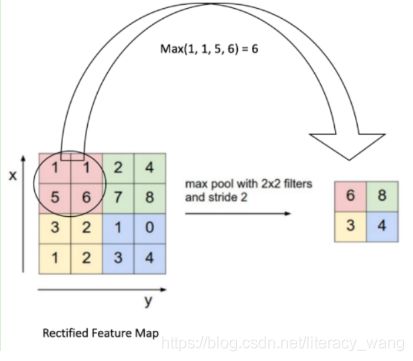
下面的例子采用取最大值MAX的池化方法，同时采用的是2×2的池化，步幅为2。

首先，对红色2×2的区域进行池化，由于此2×2区域的最大值是6。那么对应的池化输出位置的值为6，由于步幅为2，此时移动到绿色的位置取进行池化，输出的最大值为8。同样的方法，可以得到黄色区域和蓝色区域的输出值。最终，我们输入的4×4矩阵在池化后变成了2×2的矩阵，进行了压缩。

5 CNN模型小结

理解了CNN模型中的卷积层和池化层，就基本理解了CNN的基本原理。后期再讨论关于CNN模型的前向传播算法和反向传播算法。