深度学习-Graph Transformer Networks相关

Heterogeneous Graph（异质图）

图中每个节点有不同的类型，由这些节点之间关系定义的连边也有不同类型，如下例子：

区分：
同质图：图中所有节点的类型都相同，边类型只有一种的标准图

meta-path（元路径）

沿着节点的多跳路径，例如$PVP,PFP,IAP$

针对元路径的attention

主要参考Graph Transformer Networks, Heterogeneous Graph Transformer, Path-Augmented Graph Transformer Network几篇文章：attention的计算主要参考Transformer结构，在元路径的生成和相似度计算上有些不同。

1. Heterogeneous Graph Transformer：

研究动机

现有的GNN方法的不足（以HAN, GTNs, HetGNN等方法为例）：

• 大多数方法需要为异质图设计元路径（GTNs除外）；
• 要不就是假定不同类别的节点/边共享相同的特征和表示空间，要不就是单独为某一类型的节点和边设计不同的不可共享的参数。这样的话不能充分捕获异质图的属性信息；
• 大多数方法都没有考虑异质图的动态特征；
• 不能建模Web-scale的异质图。

鉴于以上挑战，作者研究目标是：
（1）保留节点和边类型的有依赖关系的特征->引入attention；
（2）捕获网络的动态信息->引入相对时间编码（RTE）技术；
（3）避免自定义元路径；
（4）并且可扩展到大规模（Web-scale）的图上->设计异质的子图采样算法HGSampling。

由于(2)、(4)没有完全理解文中方法，所以暂时关注(1)、(3)

overall framework

整张异质图表示为$G(\mathcal{V},\mathcal{E},\mathcal{A},\mathcal{R})$，其中$\tau (v):\mathcal{V}\to \mathcal{A}$表示映射为某类型的节点，某类型的源节点表示为$\tau (s)$（作为Key vector），某类型的目标节点表示为$\tau (t)$（作为Query vector）；$\varphi (v):\mathcal{E}\to \mathcal{R}$表示映射为某类型的边，连接节点s和t的某类型的边表示为$\varphi (e)。$HGT模型仅将所有连接两个节点的一跳路径作为输入，不需人工定义路径，通过attention机制可以决定最重要的元路径。

如图，$H^{(l-1)}$表示来自上一层的节点表示，整个模型可以表达为：
$$H^{(l)}[t]=\sigma (A-Linea{r}_{\tau (t)}{H}^{(l)}[t])+H^{(l-1)}[t](1)$$
$$H^{(l)}[t]={\oplus }_{\forall s\in N(t)({\text{Attention}}_{HGT}(s,e,t)\otimes Messag{e}_{HGT}(s,e,t))}(2)$$
注意到(1)包括两部分，左边是来自第l层所有邻居的信息，右边是t节点本身在第(l-1)层的信息，两部分结合得到t节点在第l层的最终表示，我们需要用$A-Linea{r}_{\tau (t)}$将向量映射回t节点类型的特征分布空间。由于小世界现象，我们可以使用少数几层，就捕获到整张图中的大部分关系了；本文中，我们遍历所有两跳路径（两层HGT），利用attention针对具体的下游任务自动地、隐式地学习并抽取出更重要的“元路径”作出如下图：

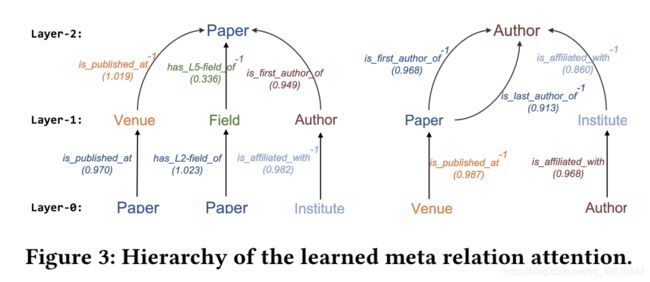
meta mutual attention

展开attention，与GAT研究同质图对比：$${\text{Attention}}_{GAT}(s,t)=Softma{x}_{\forall s\in N(t)}(v^T(W{H}^{(l-1)}[t]||W{H}^{(l-1)}[s]))$$我们在计算时假设s和t拥有相同的特征分布，所以使用了同一个投影矩阵W；但我们研究异质图时，不同类型的节点可以有不同的特征分布；
因此，我们对每种类型的源节点s使用$K-Linea{r}_{\tau (s)}$线性投影，对每种类型的目标节点t使用$Q-Linea{r}_{\tau (t)}$线性投影，同时对它们的连边使用$W_{\varphi (e)}^{ATT}$，来捕获不同的关系。注意：这里并不是参数化每种类型的边，而是根据三元关系组$<\tau (s),\varphi (e),\tau (t)>$决定，每个元关系都有一组不同的映射矩阵，整个框架高度依赖于元关系$<\tau (s),\varphi (e),\tau (t)>$来参数化权重矩阵。

这样处理后，不同类型的节点和边就可以维护其特定的表示空间。同时，通过不同的边相连的节点仍然可以交互、传递、聚合信息，并且不受它们之间分布差异的限制。 从而只将一跳的边作为输入、不人为设计元路径，也能通过跨层的信息传递来合并不同类型的高阶邻居的信息。
使用多头注意力机制表示（i上标表示第i个头获得的信息）：

• 这里使用的计算相似度方法 [Luong’s multiplicative style ]：$h_i^{T}W{h}_j$；
• 另外不同类型的边对目标节点的贡献度不同，$\mu \in {\mathbb{R}}^{|\mathcal{A}|\ast |\mathcal{R}|\ast |\mathcal{A}|}$表示基于先验知识，对三元关系组$<\tau (s),\varphi (e),\tau (t)>$的attention的缩放
• 与Transformer的区别在于：Transformer为所有的单词使用一组映射；而本文的方法中，每个元关系都有一组不同的映射矩阵

设计一系列参数的意义

（1）已有的一些方法

• 建模知识图谱的关系图卷积网络（RGCN），为每种类型的边都维护了一个线性的映射权重。
• HetGNN为不同类型的节点应用不同的RNNs来整合多模的特征。
• HAN为不同的元路径定义的边维护了不同的权重，同时使用了语义级别的注意力机制，有区分性地聚合来源于不同元路径的信息。

（2）这些方法的不足

尽管这些方法都比GCN和GAT表现好，但是它们都没有充分利用异质图的属性信息，都是为边类型和节点类型单独地分配GNN权重矩阵。但是不同类型的节点数目和不同类型的边的数目差别很大，对于那些共现次数不多的关系类型，就很难为它们学习到准确的权重。

（3）考虑参数共享以实现更好的泛化

为了解决上述问题，HGT提出参数共享。对于给定的边$e=(s,t)$其元关系为$<\tau (s),\varphi (e),\tau (t)>$。若使用三个交互矩阵分别建模 $\tau (s),\varphi (e),\tau (t)$这三个元素，则主要参数就可以共享。这样的参数共享使得出现频次较少的类型的边，也能实现快速的自适应和泛化；另一方面，使用较少的参数，仍然实现了保留不同类型边的特征。

例如“第一作者”和“第二作者”这两种关系的源节点都是author，目标节点都是paper。从一种关系学习到的author和paper的知识可以快速转换并应用到另一种关系中。

（4）HGT和现有方法的主要不同

• 与单独处理节点类型和边类型不同，作者使用元关系$<\tau (s),\varphi (e),\tau (t)>$来分解交互矩阵和转换矩阵，使得HGT在使用等量的参数甚至更少的参数的情况下，捕获不同关系中普通的和特定的信息。
• 不需要预先定义好元路径，使用神经网络框架聚合高阶的异质邻居的信息，自动地学习到元路径的重要性程度。(后面两点暂时不展开讨论)
• 大多数以往的方法没有考虑到动态图，HGT使用相对时间编码技术考虑到了时序信息。
• 现有的异质GNN方法都不能应用在Web-scale的图上，本文提出的HGSampling采样方法可以用于Web-scale图（十亿级别）的训练。

message passing

从源节点向目标节点传递信息，这一步是和互注意力的计算并行的，目的是将不同边的元关系合并到消息传递过程中，来缓解不同类型的节点和边分布的差异性。

先使用$M-Linea{r}_{\tau (s)}$将特定类型的源节点s映射成message向量，然后对特定类型的边维护一个参数矩阵$W_{\varphi (e)}^{MSG}$。

与baseline对比的一个tip： 对不同类型的节点进行线性变换，将异质数据映射到同一分布中；然后就能用处理同质图的算法来处理，最后将结果与HGT进行比较。

2.Graph Transformer Networks

研究动机

现有的GNN方法的不足：

• 采用了two-stage方法：先根据人为设定的元路径将异质图转化为同质图，再在其上面应用处理同质图的GNN算法：
• • 人为设定的元路径不能充分利用图中的信息，且将会在很大程度上影响下游任务的准确率；
• • 在固定且同质的图上进行运算，如果图上有噪声（缺失连边或者错误连边）就会导致与图上错误的邻居进行无效的卷积。

鉴于以上问题，作者研究目标是：

• 使用多个候选的原始邻接矩阵生成新的元路径图结构，在新图上进行更有效的图卷积，从而学习到更强的节点表示。

overall framework

研究的异质图同样可以表示为$G(\mathcal{V},\mathcal{E},{\mathcal{T}}^v,{\mathcal{T}}^e)$，其中$f(v):\mathcal{V}\to {\mathcal{T}}^v$表示映射为某类型的节点，$f(e):\mathcal{E}\to {\mathcal{T}}^e$表示映射为某类型的边。每个邻接矩阵$A_k$代表某一种类型的边的关系，因此假如从$v_1$到$v_{l+1}$经过的元路径为$(t_1,t_2,...,t_l)$，其中$t_l\in {\mathcal{T}}^e$，那么$v_1\stackrel{t_1}{⟶}{v}_2\stackrel{t_2}{⟶}...\stackrel{t_l}{⟶}{v}_{l+1}$可以由一系列邻接矩阵的矩阵乘法表示：
$$A_P=A_{t_l}...A_{t_2}{A}_{t_1}$$

一个前提：
对于无向图GCN的卷积操作表示为：
$$H^{(l+1)}=\sigma (D^{\frac{-1}{2}}A{D}^{\frac{-1}{2}}{H}^{(l)}{W}^{(l)})$$
对于有向图表示为：
$$H^{(l+1)}=\sigma (D^{-1}A{H}^{(l)}{W}^{(l)})$$
可见GCN是在固定且同质的图上进行卷积操作，只有针对节点的线性转换参数$H^{(l)}{W}^{(l)}$是可学习的。

整个模型架构可以看成是：在由GT层学习到的多个元路径图上进行GCN，从而解决节点分类任务。

1.使用attention机制筛选邻接矩阵$Q_{t_l}$：

（注：图中的例子特指元路径为2的情况，因此选出分别表示两种类型的边的邻接矩阵）GT层从候选的邻接矩阵$\mathbb{A}$（每一片都代表一种边类型）中选择出两个图结构$Q_1,Q_2$；每一个被选出来的图结构都可以看成是在原邻接矩阵$\mathbb{A}$上应用了attention，为各个片分配了不同的权重，加权求和得到新的邻接矩阵$Q_{t_l}=\sum _{t_l\in {\mathcal{T}}^e}{\alpha }_{t_l}^{(l)}{A}_{t_l}$；

2.将选择出的邻接矩阵$Q_i$组合得到新的图结构：

采用矩阵相乘得到新的邻接矩阵$A^{(l)}=Q_1{Q}_2$；
为了数值稳定，使用度矩阵进行归一化$A^{(l)}=D^{-1}{Q}_1{Q}_2$；由此可以进一步推广：长度为l的元路径对应的邻接矩阵$A_P$可以表示为堆叠l层GT层：
$$A_P=(\sum _{t_1\in {\mathcal{T}}^e}{\alpha }_{t_1}^{(1)}{A}_{t_1})(\sum _{t_2\in {\mathcal{T}}^e}{\alpha }_{t_2}^{(2)}{A}_{t_2})...(\sum _{t_l\in {\mathcal{T}}^e}{\alpha }_{t_l}^{(l)}{A}_{t_l})$$
采用归一化表达为：


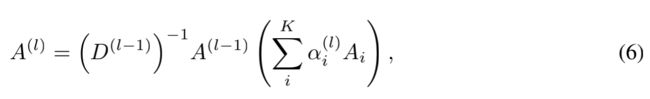
即元路径$(t_1,t_2,...,t_l)$的贡献度计算为${\prod }_{i=0}^l{\alpha }_{t_i}^l$，这个贡献度就代表了在预测任务中某条特定元路径的重要性。因此GTN可以自适应地学习到对特定任务较重要的元路径。

由于生成的元路径长度等于GT层的层数，堆叠的层数越多，生成的元路径越长；堆叠多层后原始图中的连边可能不存在了，但实际上有的时候短的元路径也很重要。
为了学习到包含原始图中连边的长的元路径和短的元路径，在$\mathbb{A}$中加入单位矩阵$I$，即$A_0=I$，这样，当有l层GT层时，就可以学习到长度为$1\sim l$的元路径。

为了同时生成多种类型的元路径，将图1中卷积的输出通道设置为C，表示生成C条元路径，l表示生成的元路径的最大长度。在l个GT层堆叠后，将GCN应用于元路径张量 ${\mathbb{A}}^l\in R^{N\times N\times C}$的每个通道，并将多个节点的向量表示拼接起来：
$$Z=|{|}_{i=1}^C\sigma (D_i^{-1}{A}_i^{l}XW)$$
其中$A_i^{(l)}$是${\mathbb{A}}^{(l)}$第i个通道的邻接矩阵，$D_i^{-1}$是$A_i^{(l)}$的度矩阵
此时Z代表了节点在C个元路径图中的表示，且元路径的长度最长为l，将Z用于有监督的节点分类任务，分类器的结构为：输入到两层稠密层，经过一层softmax，损失函数使用交叉熵函数。 因此，整个模型架构可以看成是：在由GT层学习到的多个元路径图上进行GCN，从而解决节点分类任务。

---

参考

【论文解读 WWW 2020 | HGT】Heterogeneous Graph Transformer
【论文解读 NIPS 2019 | GTNs】Graph Transformer Networks