神经网络（NN）网络构建及模型算法介绍

概述

神经网络最主要的作用是作为提取特征的工具，最终的分类并不是作为主要核心。

人工神经网络也称为多层感知机，相当于将输入数据通过前面多个全连接层网络将原输入特征进行了一个非线性变换，将变换后的特征拿到最后一层的分类器去分类。

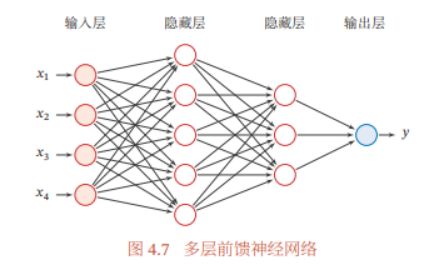
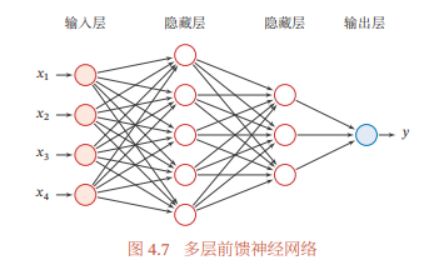
神经网络是由多个神经元组成的拓扑结构，由多个层排列组成，每一层又堆叠了多个神经元。通常包括输入层，N个隐藏层，和输出层组成。

输出层：分类任务中如果是二分类任务输出层只需要1个神经元，如果是K个分类问题，输出层要有K个神经元。对输出层的每个神经元代入分类函数就可以得到每个分类的概率大小，取最大概率的作为分类结果。对于多分类问题的分类器模型常采用Softmax回归模型，即多分类问题的Logistic回归模型。

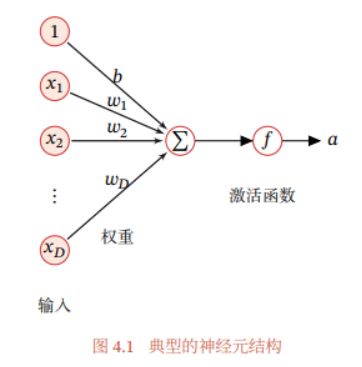
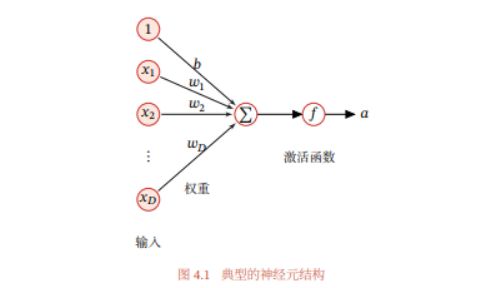
输入层：以一个128x128像素的图像为例，人工神经网络只能处理一维的数据。所以要把图像按顺序展开为一维的像素数据。即（1，16384）1行和16384列的数据也是16384个特征。输入层的每个神经元仅接收一个输入特征，因此输入层的神经元个数和图像的特征数也即像素个数一样有16384个。那么每个神经元的1个输入需要求1个权重w，每个神经元要求一个参数b，因此输入层的待求参数就有16384x2 =32768。

隐藏层：中间的每层隐藏层可以根据需求设置多个神经元。其中每个神经元都要输入和前一层神经元的个数个输入特征。输入层比较特殊一个神经元只对应一个输入X,中间隐藏层每个神经元对应输入前一层所有神经元的个数个x。假如该隐藏层有328个神经元组成。连接的前一层是输入层有128x128=16384个神经元。那么每个神经元都对应16384个输入x,因此一个神经元的待求参数量为16384个w和1个b,那么该层所有的待求参数量为：（16384+1）x328=5,374,280‬个待求参数。可见人工神经网络的参数量非常多，难以计算而且很容易过拟合。                                               

1、前馈神经网络具有很强的拟合能力，常见的连续非线性函数都可以用前馈 神经网络来近似．

2、根据通用近似定理，神经网络在某种程度上可以作为一个“万能”函数来使 用，可以用来进行复杂的特征转换，或逼近一个复杂的条件分布

3、一般是通过经验风险最小化和正则化来 进行参数学习．因为神经网络的强大能力，所以容易在训练集上过拟合．

4、神经网络的优化问题是一个非凸优化问题，而且可能面临梯度消失的问题。

单个神经元模型： 

神经网络结构： 

 

主要内容

神经元的模型：

 在前馈神经网络中，各神经元分别属于不同的层．每一层的神经元可以接收 前一层神经元的信号，并产生信号输出到下一层．第0层称为输入层，最后一层称 为输出层，其他中间层称为隐藏层．整个网络中无反馈，信号从输入层向输出层 单向传播，可用一个有向无环图表示．

前馈神经网络结构

 

神经网络的本质是可以对输入特征进行任意复杂的非线性变换转换为易分类特征

前馈神经网络具有很强的拟合能力，常见的连续非线性函数都可以用前馈 神经网络来近似．

根据通用近似定理，对于具有线性输出层和至少一个使用“挤压”性质的激 活函数的隐藏层组成的前馈神经网络，只要其隐藏层神经元的数量足够，它可 以以任意的精度来近似任何一个定义在实数空间 ℝ

通用近似定理只是说明了神经网络的计算能力可以去近似一个给定的连续 函数，但并没有给出如何找到这样一个网络，以及是否是最优的．此外，当应用到 机器学习时，真实的映射函数并不知道，一般是通过经验风险最小化和正则化来 进行参数学习．因为神经网络的强大能力，反而容易在训练集上过拟合．

根据通用近似定理，神经网络在某种程度上可以作为一个“万能”函数来使 用，可以用来进行复杂的特征转换，或逼近一个复杂的条件分布

在机器学习中，输入样本的特征对分类器的影响很大．以监督学习为例，好 的特征可以极大提高分类器的性能．因此，要取得好的分类效果，需要将样本的 原始特征向量，这个过程叫作特征抽取．

多层前馈神经网络可以看作一个非线性复合函数 ，将输入映射到输出．因此，多层前馈神经网络也可以看成是一种特 征转换方法，其输出

作为分类器的输入进行分类． 

（1）网络模型

 原输入特征经过多层隐藏层网络的非线性变换后                                                                             在最后输出层后面使用一个常用的传统机器学习分类器进行分类

 

***以上内容讲解了神经网络的结构，以及模型公式原理，怎样从输入数据x构建模型到输出y。           对应实战课程中构建模型的第一步，及其原理的讲解。

（2）构建损失函数，参数学习

完成了第一步，有了模型，下一步就是构建用于优化的损失函数，利用损失函数来优化出网络中所有的待求参数w和b

常用的损失函数使用过的是交叉熵损失函数，求其最小化

 yt对应真实标签，y_是模型预测的结果

（3）有了损失函数就可以根据实际的需要选择合适的优化器迭代优化上面的损失函数

（4）在实战应用中最后要构建模型评价指标如测试准确率，来监控模型训练的状态

优化过程采用反向传播来逐步更新参数梯度值，实际应用中各平台都支持自动梯度计算，这里暂不讲解。

补充：

神经网络的参数学习比线性模型要更加困难，

主要原因有两点：1）非凸优 化问题和2）梯度消失问题．

神经网络的优化问题是一个非凸优化问题

 

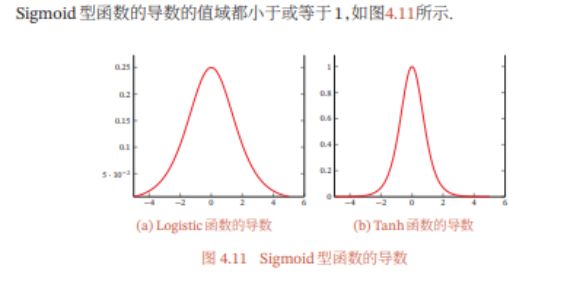
这样，误差经 过每一层传递都会不断衰减．当网络层数很深时，梯度就会不停衰减，甚至消 失，使得整个网络很难训练．这就是所谓的梯度消失问题（Vanishing Gradient Problem），也称为梯度弥散问题．

由于 Sigmoid 型函数的饱和性，饱和区的导数更是接近于 0

在深度神经网络中，减轻梯度消失问题的方法有很多种．一种简单有效的方 式是使用导数比较大的激活函数，比如ReLU等．