graphviz 画决策树_数据挖掘入门系列教程(四)之基于scikit-lean决策树处理Iris
- 数据挖掘入门系列教程(四)之基于scikit-lean决策树处理Iris
- 加载数据集
- 数据特征
- 训练
- 随机森林
- 调参工程师
- 结尾
数据挖掘入门系列教程(四)之基于scikit-lean决策树处理Iris
在上一篇博客,我们介绍了决策树的一些知识。如果对决策树还不是很了解的话,建议先阅读上一篇博客,在来学习这一篇。
本次实验基于scikit-learn中的Iris数据。说了好久的Iris,从OneR到决策树,那么Iris到底长啥样呢?
加载数据集
首先我们还是需要先加载数据集,数据集来自scikit自带的iris数据集,数据集的内容可以参考以前的博客,这里就不在赘述。
首先让我们从scikit-learn中加载数据集。
from sklearn.datasets import load_iris
dataset = load_iris()
data = dataset.data
target = dataset.target然后我们再使用pandas将数据进行格式化以下,添加Iris的属性到数据集中。
import numpy as np
import pandas as pd
data = pd.DataFrame(data,columns=["sepal_length","sepal_width","petal_length","petal_width"])
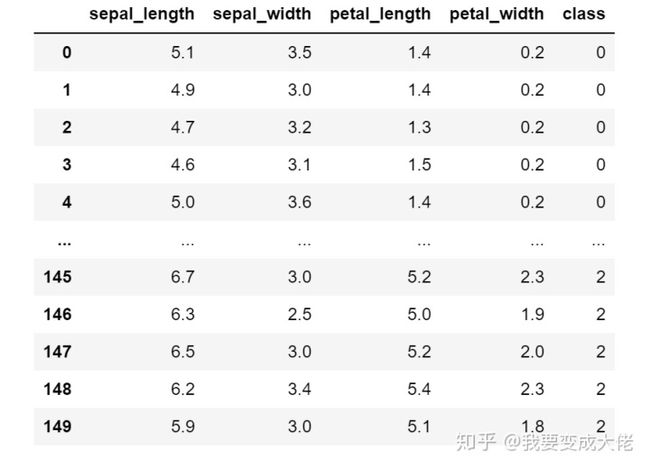
data["class"] = targetdata的数据如下所示:
class代表类别。其他的就是Iris的属性了。
数据特征
这里我们主要是用画图来看一看Iris数据集的特征。本来以为画图就matpotlib就行了,但是没想到有seaborn这个好使用的库,来自B站up主的提示。使用的库如下:
- matplotlib
- seaborn
首先我们画散点图:
import matplotlib.pyplot as plt
import seaborn as sb
# data.dropna()去除里面的none元素
sb.pairplot(data.dropna(),hue="class")图像如下所示:
上面的这幅图展示了在四个属性中的类别的分别情况。
同时我们还可以画小提琴图:
plt.figure(figsize=(20, 20))
for column_index, column in enumerate(data.columns):
if column == 'class':
continue
plt.subplot(2, 2, column_index + 1)
sb.violinplot(x='class', y=column, data=data)画出的图如下:
通过上面的这幅图我们可以直观的比较出哪一个变量更具有代表性。比如说petal_width 对类别0更加的友好。
接下来就是进行训练了。
训练
首先的首先,我们还是需要从数据集中抽出训练集和测试集。这个内容在前面讲过了,就不多讲了。
from sklearn.model_selection import train_test_split
input_data = data[["sepal_length","sepal_width","petal_length","petal_width"]]
input_class = data["class"]
train_data,test_data,train_class,test_class = train_test_split(input_data,input_class,random_state = 14)then,让我们来开始进行训练吧,在scikit-learn中实现了决策树,和前面的K近邻算法一样我们直接引用就行,调用fit(训练)和predict(预测)函数。使用如下所示:
from sklearn.tree import DecisionTreeClassifier
decision_tree = DecisionTreeClassifier(random_state=14)
decision_tree.fit(train_data,train_class)
predict_class = decision_tree.predict(test_data)
predict_score = np.mean(predict_class == test_class)
print("预测的准确度为{}".format(predict_score))DecisionTreeClassifier其他的参数在后面说,这里主要说一下random_state参数。为什么决策树还需要random_state这个参数,以下知乎上面的两位博主的说法。
至于哪个说法是正确的,我暂时也不知道,如果有知道的,可以在评论区留言哦!
最后得到的预测结果如下所示:
这里值得注意的是DecisionTreeClassifier()函数,里面可以添加很多参数。官方文档在这里: https://scikit-learn.org/stable/modules/generated/sklearn.tree.DecisionTreeClassifier.html 。
这里还是稍微的说一下参数。
# criterion gini(默认)/tropy:这里对应的就是之前的熵增益和Gini系数
# splitter best(默认)/random 每个结点选择的拆分策略
# max_depth 树的最大深度。
# min_samples_split int类型或者float(默认2) 如果某节点的样本数少于min_samples_split,则不会进行拆分了。浮点值表示分数,代表所占比例
# min_samples_leaf 默认=1 这个值限制了叶子节点最少的样本数,如果某叶子节点数目小于样本数,则会和兄弟节点一起被剪枝。
# min_weight_fraction_leaf float(默认0.0) 这个值限制了叶子节点所有样本权重,如果小于这个值,则会和兄弟节点一起被剪枝。一般来说,如果我们有较多样本有缺失值,或者分类树样本的分布类别偏差很大,就会引入样本权重,这时我们就要注意这个值了。
# max_features int, float or {“auto”, “sqrt”, “log2”}(默认0.0)
# max_leaf_nodes 通过限制最大叶子节点数,可以防止过拟合,默认是"None”,即不限制最大的叶子节点数。如果加了限制,算法会建立在最大叶子节点数内最优的决策树。
# class_weight dict/balanced 指定样本各类别的的权重,主要是为了防止训练集某些类别的样本过多导致训练的决策树过于偏向这些类别。这里可以自己指定各个样本的权重。“balanced”,则算法会自己计算权重,样本量少的类别所对应的样本权重会高。
# min_impurity_split 这个值限制了决策树的增长,如果某节点的不纯度(基尼系数,信息增益,均方差,绝对差)小于这个阈值则该节点不再生成子节点。即为叶子节点 。更多的可以去看官网细节。
然后我们可以将这个树的结构可视化,将文件保存在“tree.dot”中:
from sklearn.tree import export_graphviz
with open("tree.dot",'w') as f:
export_graphviz(decision_tree, feature_names =['sepal_length', 'sepal_width', 'petal_length', 'petal_width'], out_file = f)这个是决策树的图:
同样,我们还可以使用交叉验证,具体的使用可以参考别人的博客,或者看我的这一篇博客:
from sklearn.model_selection import cross_val_score
decision_tree = DecisionTreeClassifier()
scores = cross_val_score(decision_tree,input_data,input_class,scoring='accuracy')
print("交叉验证结果: {0:.2f}%".format(np.mean(scores) * 100))通过交叉验证得到的准确度如下:
比上面的结果略低,不过这个是正常的。
随机森林
前面的博客介绍了随机树,这里不多做介绍,直接看使用吧。我们通过导入RandomForestClassifier模块,并指令森林中树的个数为30,具体的参数看官网
from sklearn.ensemble import RandomForestClassifier
rft = RandomForestClassifier(n_estimators=20,random_state=14)
rft.fit(train_data,train_class)
predict_class = rft.predict(test_data)
predict_score = np.mean(predict_class == test_class)
print("随机森林预测的准确度为{}".format(predict_score))最后的结果如下图
然后进行交叉验证:
scores = cross_val_score(rft,input_data,input_class,scoring='accuracy')
print("Accuracy: {0:.2f}%".format(np.mean(scores) * 100))结果如下:
emm,好像和上面的结果一样,因为这个数据集很小,可能会有这种情况。
调参工程师
首先,我们可以对决策树的max_feature和max_depth进行调参,改变其值,最终的结果如下:
在随机森林中,我们可以对树的个数进行调参,结果如下图:
结尾
这次并没有使用《 Python数据挖掘入门与实践 》书上的例子,实在是它打篮球的数据找不到,emm。相比较与oneR算法的70%左右的正确率,决策树95%正确率已经算足够优秀了。
尽管代码写起来很简单,也很容易实现得到结果,但是我们真正应该了解的是里面的内涵:决策树是什么?里面是怎样工作的?以及所蕴含的含义……
项目地址:GitHub