《机器学习》及实战四、贝叶斯理论及实战
- Python版本: Python3.x
- 运行平台: Windows
- IDE: PyCharm
- 参考资料:《机器学习》(西瓜书)《机器学习实战》(王斌)
- 转载请标明出处:https://blog.csdn.net/tian121381/category_9748511.html
- 资料下载,提取码:j2l5
目录
- 一、前言
- 二、贝叶斯的理论知识
-
-
- 1. 链接学习
- 2. 手算预测
- 3. 拉普拉斯修正
-
- 三、 构造简单的朴素贝叶斯
-
-
- 1. 收集数据
- 2. 准备数据
- 3. 训练算法
- 4. 分类函数
- 5. 测试朴素贝叶斯
-
- 四、 实例—垃圾邮件的过滤
-
-
- 1. 准备数据:切分文本
- 2. 文本向量化
- 3. 训练算法
- 4. 分类函数
- 5. 测试分类器
-
- 五 、 新闻分类(SKlearn)
-
-
- 1. 处理数据
- 2. 分析数据
- 3. sklearn构造贝叶斯分类器
- 4. 参数调试
- 5. 使用分类器
-
- 六 、 总结
一、前言
前两章我们要求分类器做出艰难决策,给出“该数据实例属于哪⼀类”这类问题的明确答案。不过,分类器有时会产⽣错误结果,这时可以要求分类器给出⼀个最优的类别猜测结果,同时给出这个猜测的概率估计值。 概率论是许多机器学习算法的基础,所以深刻理解这一主题就显得⼗分重要。第3章在计算特征值取某个值的概率时涉及了⼀些概率知识,在那里我们先统计特征在数据集中取某个特定值的次数,然后除以数据集的实例总数,就得到了特征取该值的概率。我们将在此基础上深⼊讨论(概率论的相关知识忘记的可以去复习下,只用到了条件概率)。 本章会给出⼀些使⽤概率论进⾏分类的⽅法。⾸先从 ⼀个最简单的概率分类器开始,然后给出⼀些假设来学习朴素贝叶斯分类器。我们称之为“朴素”,是因为整个形式化过程只做最原始、最简单的假设,这章咱们主要讲的也是朴素贝叶斯。
二、贝叶斯的理论知识
1. 链接学习
贝叶斯决策论(Bayesian decision theory)是概率框架下实施决策的基本方法。我看了两篇文章,感觉很好,很适合第一次接触贝叶斯分类器的同学,它可以让我们直观的理解,肯定比我说的要好,可以去看一下。
非数学语言讲解贝叶斯定理
朴素贝叶斯分类算法
2. 手算预测
看完上面链接的内容,相信你们对贝叶斯有了个大体的理解了。我再举个例子加深一下印象(随便补充点)。(~ ̄▽ ̄)~
有如下数据集。

假定通过上面的数据集训练了一个贝叶斯分类器,再给你一个测试集,你会判断它的类型嘛?如下面的测试集。

可否知道这个瓜是不是好瓜呢?先说一下思路,咱们的目的是分别求好瓜的条件下满足上述条件的,坏瓜的条件下满足上述条件的。再判断谁的概率大,就是什么瓜。
通过分享的链接的内容知,第一步要先计算先验概率 P( c ), 显然有

然后,为每个属性估计条件概率 P(xi |c) :

要注意到密度和含糖率不是离散型的数据,而是连续的。
对连续属性可考虑概率密度函数,如下
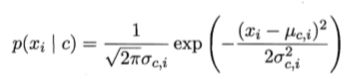
其中 μ和σ^2分别是第 c 类样本在第 i个属性上取值的均值和方差。(还要求方差,好麻烦的有没有)

于是,有

由于 0.038 > 6.80 x 10^-5,因此7,朴素贝叶斯分类器将测试样本"测 1" 判别为 “好瓜”。
3. 拉普拉斯修正
需注意,若某个属性值在训练集中没有与某个类同时出现过,则直接进行概率估计,进行判别将出现问题。例如,在使用西瓜数据集中,训练朴素贝叶斯分类器时,对一个"敲声=情脆"的测试例,有

那代入累乘后,不就全是0了嘛,没意义了。
为了避免其他属性携带的信息被训练集中未出现的属性值"抹去’,在估计概率值时通常要进行"平滑" (smoothing),常用"拉普拉斯修正" 。具体来说,令 N 表示训练集 D 中可能的类别数,Ni表示第 i个属性可能的取值数,那公式就修正为
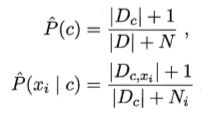
也是这个例子,它们就变成了
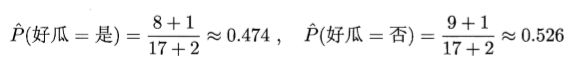

![]()
![]()
显然,拉普拉斯修正避免了因训练集样本不充分而导致概率估值为零的问题, 并且在训练集变大时,修正过程所引入的先验(prior)的影响也会逐渐变得可忽略,使得估值渐趋向于实际概率值。
到目前为止,咱们已经了解了足够的知识,可以开始编写代码了。如果还不清楚,那么了解代码的实际效果会有助于理解。
三、 构造简单的朴素贝叶斯
朴素贝叶斯的⼀般过程:
- 收集数据:置顶资料下载处。
- 准备数据:需要数值型或者布尔型数据
- 分析数据:有⼤量特征时,绘制特征作用不大,此时使⽤直⽅图效果更好。
- 训练算法:计算不同的独立特征的条件概率。
- 测试算法:计算错误率。
- 使⽤算法:⼀个常见的朴素贝叶斯应用是文档分类。可以在任意的分类场景中使用朴素贝叶斯分类器,不⼀定非要是文本。
以在线社区的留⾔板为例。为了不影响社区的发展,我们要屏蔽侮辱性的⾔论,所以要构建⼀个快速过滤器,如果某条留⾔使⽤了负⾯或者侮辱性的语⾔,那么就将该留⾔标识为内容不当。过滤这类内容是⼀个 很常见的需求。对此问题建⽴两个类别:侮辱类和非侮辱类,使⽤1和0分别表⽰。 接下来首先给出将⽂本转换为数字向量的过程,然后介绍如何基于这些向量来计算条件概率,并在此基础上构建分类器,最后还要介绍⼀些利⽤Python实现朴素贝叶斯过程中需要考虑的问题。
1. 收集数据
本例自写了几个简单数据。
2. 准备数据
先引入相关包
import numpy as np
from functools import reduce
因为咱们一开始构造简单的,先自己写几个句子,和它们是否是侮辱性的标签向量。
def loadDataSet():
"""
Parameters:
无
Returns:
postingList - 实验样本切分的词条
classVec - 类别标签向量
"""
postingList=[['my', 'dog', 'has', 'flea', 'problems', 'help', 'please'], #切分的词条
['maybe', 'not', 'take', 'him', 'to', 'dog', 'park', 'stupid'],
['my', 'dalmation', 'is', 'so', 'cute', 'I', 'love', 'him'],
['stop', 'posting', 'stupid', 'worthless', 'garbage'],
['mr', 'licks', 'ate', 'my', 'steak', 'how', 'to', 'stop', 'him'],
['quit', 'buying', 'worthless', 'dog', 'food', 'stupid']]
classVec = [0, 1, 0, 1, 0, 1] #类别标签向量,1代表侮辱性词汇,0代表不是
return postingList, classVec
#------测试-------------------------------------------------------
if __name__ == '__main__':
postingLIst, classVec = loadDataSet()
for each in postingLIst:
print(each)
print(classVec)
结果:
['my', 'dog', 'has', 'flea', 'problems', 'help', 'please']
['maybe', 'not', 'take', 'him', 'to', 'dog', 'park', 'stupid']
['my', 'dalmation', 'is', 'so', 'cute', 'I', 'love', 'him']
['stop', 'posting', 'stupid', 'worthless', 'garbage']
['mr', 'licks', 'ate', 'my', 'steak', 'how', 'to', 'stop', 'him']
['quit', 'buying', 'worthless', 'dog', 'food', 'stupid']
[0, 1, 0, 1, 0, 1]
将切分的实验样本词条整理成不重复的词条列表,也就是词汇表。
def createVocabList(dataSet):
vocabSet = set([]) #创建空的不重复的列表
for document in dataSet: #遍历所有句子,找并集
#vocabSet = set(vocabSet.union(document)) #取并集
vocabSet = vocabSet | set(document) # 取并集
#print('aaa',vocabSet)
return list(vocabSet)
#-------测试-----------------------------------------
if __name__ == '__main__':
postingList, classVec = loadDataSet()
print('postingList:\n',postingList)
myVocabList = createVocabList(postingList)
print('myVocabList:\n',myVocabList)
结果:
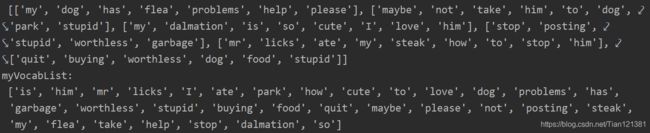
根据vocabList词汇表,将inputSet向量化,向量的每个元素为1或0。简单点的意思就是我们把输入的句子放入前面求得的有所有单词的词汇表。将输入句子里有的单词,在词汇表里置1,没有的为默认0。代码如下
def setOfWords2Vec(vocabList,inputSet):
returnVec = [0] * len(vocabList) #创建一个其中所含元素都为0的向量,默认0
for word in inputSet: #遍历每个词条
if word in vocabList: #如果词条存在于词汇表中,则置1
returnVec[vocabList.index(word)] = 1
else:
print("the word: %s is not in my Vocabulary!" % word)
return returnVec
#----------测试-----------------------------------------------------
if __name__ == '__main__':
postingList, classVec = loadDataSet()
print('postingList:\n',postingList)
myVocabList = createVocabList(postingList)
print('myVocabList:\n',myVocabList)
trainMat = []
for postinDoc in postingList: #将我们写的句子改写为0 1格式
trainMat.append(setOfWords2Vec(myVocabList,postinDoc))
print('trainMat:\n', trainMat)
结果:
postingList:
[['my', 'dog', 'has', 'flea', 'problems', 'help', 'please'], ['maybe', 'not', 'take', 'him', 'to', 'dog', 'park', 'stupid'], ['my', 'dalmation', 'is', 'so', 'cute', 'I', 'love', 'him'], ['stop', 'posting', 'stupid', 'worthless', 'garbage'], ['mr', 'licks', 'ate', 'my', 'steak', 'how', 'to', 'stop', 'him'], ['quit', 'buying', 'worthless', 'dog', 'food', 'stupid']]
myVocabList:
['cute', 'maybe', 'problems', 'steak', 'love', 'buying', 'posting', 'ate', 'so', 'I', 'has', 'my', 'flea', 'not', 'to', 'mr', 'how', 'stupid', 'take', 'dog', 'is', 'licks', 'him', 'worthless', 'dalmation', 'park', 'quit', 'please', 'help', 'stop', 'food', 'garbage']
trainMat:
[[0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 1, 1, 1, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 1, 1, 0, 0, 0],
[0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 1, 0, 0, 1, 1, 1, 0, 0, 1, 0, 0, 1, 0, 0, 0, 0, 0, 0],
[1, 0, 0, 0, 1, 0, 0, 0, 1, 1, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 1, 0, 1, 0, 0, 0, 0, 0, 0, 0],
[0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 1, 0, 1],
[0, 0, 0, 1, 0, 0, 0, 1, 0, 0, 0, 1, 0, 0, 1, 1, 1, 0, 0, 0, 0, 1, 1, 0, 0, 0, 0, 0, 0, 1, 0, 0],
[0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 1, 0, 0, 0, 1, 0, 0, 1, 0, 0, 0, 1, 0]]
和前面的对一下,看看对吗,0,1的位置与单词位置是否一致。
从运行结果可以看出,postingList是原始的词条列表,myVocabList是词汇表。myVocabList是所有单词出现的集合,没有重复的元素。词汇表是用来干什么的?没错,它是用来将词条向量化的,一个单词在词汇表中出现过一次,那么就在相应位置记作1,如果没有出现就在相应位置记作0。trainMat是所有的词条向量组成的列表。它里面存放的是根据myVocabList向量化的词条向量。
3. 训练算法
前⾯介绍了如何将⼀组单词转换为⼀组数字,接下来看看如何使⽤这些数字计算概率。。现在已经知道⼀个词是否出现在⼀则留言中,也知道该留言所属的类别。通过贝叶斯相关公式。
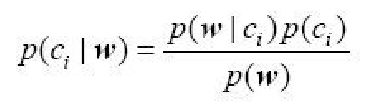
其中。w表示这是⼀个向量,即它由多个数值组成。
我们将使用上述公式,对每个类计算该值,然后⽐较这两个概率值的大小。如何计算呢?首先可以通过类别 i(侮辱性留⾔或⾮侮辱性留⾔)中⽂档数除以总的⽂档数来计算概率p(ci)。接下来计算p(w|ci),这里就要⽤到朴素贝叶斯假设。如果将w展开为⼀个个独立特征,那么就可以将上述概率写 作p(w0,w1,w2…wN|ci)。这⾥假设所有词都互相独⽴, 该假设也称作条件独立性假设,它意味着可以使用p(w0|ci)p(w1|ci)p(w2|ci)…p(wN|ci)来计算上述概率,这就极大地简化了计算的过程。
该函数的伪代码如下:

知道思路和流程了,下面就是代码了。
def trainNB0(trainMatrix,trainCategory):
"""
Parameters:
trainMatrix - 训练文档矩阵,即setOfWords2Vec返回的returnVec构成的矩阵
trainCategory - 训练类别标签向量,即loadDataSet返回的classVec
Returns:
p0Vect - 侮辱类的条件概率数组
p1Vect - 非侮辱类的条件概率数组
pAbusive - 文档属于侮辱类的概率
"""
#文档的数量
numtrainDocs = len(trainMatrix)
#每篇文档的词条数
numWords = len(trainMatrix[0])
#文档属于侮辱类的概率
pAbusive = sum(trainCategory) / float(numtrainDocs) #训练集是0,1分类的,1是侮辱类,累加就是侮辱类的个数
# 创建numpy.zeros数组,词条出现数初始化为0
#p0Num = np.zeros(numWords); p1Num = np.zeros(numWords) #会出现概率0的情况,如理论部分所说。
p0Num = np.ones(numWords); p1Num = np.ones(numWords) #创建numpy.ones数组,词条出现数初始化为1,拉普拉斯平滑
p0Denom = 2.0; p1Denom = 2.0 #分母初始化为2,拉普拉斯平滑
for i in range(numtrainDocs):
#统计属于侮辱类的条件概率所需的数据,即P(w0|1),P(w1|1),P(w2|1)···
if trainCategory[i] == 1: # 统计属于侮辱类的条件概率所需的数据,即P(w0|1),P(w1|1),P(w2|1)···
p1Num += trainMatrix[i] #词条出现的次数统计
#print('aaa', p1Num)
p1Denom += sum(trainMatrix[i]) #侮辱类词语总数
#print('bbb', p1Denom)
else: # 统计属于非侮辱类的条件概率所需的数据,即P(w0|0),P(w1|0),P(w2|0)···
p0Num += trainMatrix[i]
p0Denom += sum(trainMatrix[i])
#分别求各自条件下,各单词出现的概率
p1Vect = np.log(p1Num / p1Denom)
p0Vect = np.log(p0Num / p0Denom) #取对数防止下溢,一会会说。
# print('aaa',p1Num)
# print('bbb',p1Denom)
return p0Vect,p1Vect,pAbusive
#-----------测试-----------------------
if __name__ == '__main__':
postingList, classVec = loadDataSet()
myVocabList = createVocabList(postingList)
print('myVocabList:\n', myVocabList) #词汇表
trainMat = []
for postinDoc in postingList:
trainMat.append(setOfWords2Vec(myVocabList, postinDoc)) #向量化
p0V, p1V, pAb = trainNB0(trainMat, classVec)
print('p0V:\n', p0V)
print('p1V:\n', p1V)
print('classVec:\n', classVec)
print('pAb:\n', pAb)
结果:
myVocabList:
['park', 'dalmation', 'how', 'stop', 'please', 'cute', 'quit', 'dog', 'stupid', 'I', 'posting', 'licks', 'take', 'has', 'so', 'flea', 'garbage', 'not', 'help', 'mr', 'worthless', 'buying', 'problems', 'is', 'food', 'to', 'steak', 'maybe', 'him', 'love', 'my', 'ate']
p0V:
[-3.25809654 -2.56494936 -2.56494936 -2.56494936 -2.56494936 -2.56494936
-3.25809654 -2.56494936 -3.25809654 -2.56494936 -3.25809654 -2.56494936
-3.25809654 -2.56494936 -2.56494936 -2.56494936 -3.25809654 -3.25809654
-2.56494936 -2.56494936 -3.25809654 -3.25809654 -2.56494936 -2.56494936
-3.25809654 -2.56494936 -2.56494936 -3.25809654 -2.15948425 -2.56494936
-1.87180218 -2.56494936]
p1V:
[-2.35137526 -3.04452244 -3.04452244 -2.35137526 -3.04452244 -3.04452244
-2.35137526 -1.94591015 -1.65822808 -3.04452244 -2.35137526 -3.04452244
-2.35137526 -3.04452244 -3.04452244 -3.04452244 -2.35137526 -2.35137526
-3.04452244 -3.04452244 -1.94591015 -2.35137526 -3.04452244 -3.04452244
-2.35137526 -2.35137526 -3.04452244 -2.35137526 -2.35137526 -3.04452244
-3.04452244 -3.04452244]
classVec:
[0, 1, 0, 1, 0, 1]
pAb:
0.5
这里不要困惑,我的p0V,p1V是概率呀,为什么会是负数呢?因为咱们取对数了,为什么要这么取呢?看下图。
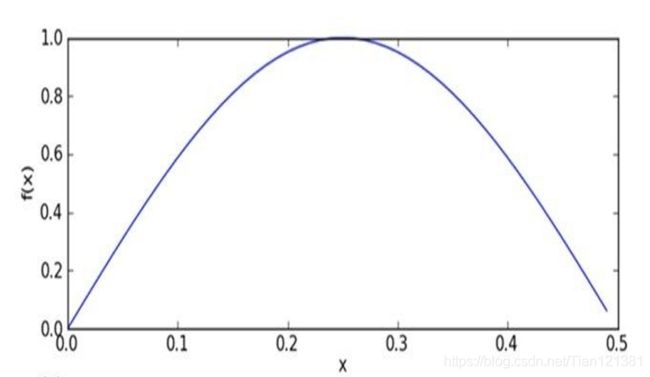
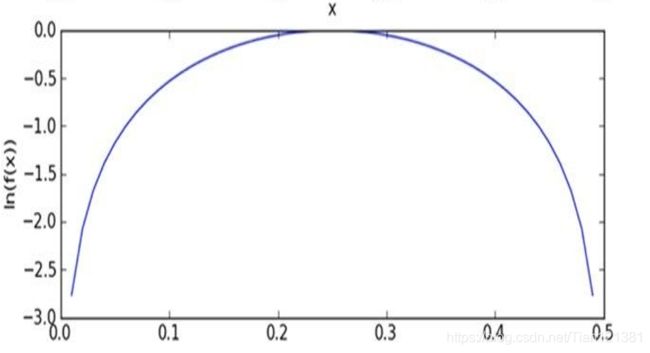
由于太多很小的数(概率肯定小于1,而且越乘越小)相乘可能造成下溢出。当计算乘积 p(w0|ci)p(w1|ci)p(w2|ci)…p(wN|ci)时,由于大部分因子都非常小,所以程序会下溢出或者得到不正确的答案。⼀种解决办法是对乘积取⾃然对数。在代数中有ln(a*b) = ln(a)+ln(b),于是通过求对数可以避免下溢出或者浮点数舍⼊导致的错误。同时,采⽤自然对数进⾏处理不会有任何损失。 上给出函数f(x)与ln(f(x))的曲线。检查这两条曲线,就会发现它们在相同区域内同时增加或者减少, 并且在相同点上取到极值。它们的取值虽然不同,但不影响最终结果。
所以p0,p1概率那样求。
4. 分类函数
训练好分类器,接下来,使用分类器进行分类。
相关函数介绍:
reduce(lambda x, y: x * y, lst) lamda表达式,对lst里面的参数进行处理
p1 = reduce(lambda x,y:xy,vec2Classify * p1Vec) * pClass1 对应元素相加
p0 = reduce(lambda x,y: xy,vec2Classify * p0Vec) * (1.0 - pClass1)
def classifyNB(vec2Classify,p0Vec,p1Vec,pClass1):
"""
Parameters:
vec2Classify - 待分类的词条数组
p0Vec - 侮辱类的条件概率数组
p1Vec - 非侮辱类的条件概率数组
pClass1 - 文档属于侮辱类的概率
Returns:
0 - 属于非侮辱类
1 - 属于侮辱类
"""
#对应拉普拉斯修正,因为取自然对数了。logab = loga + logb。
# 对应元素相乘。logA * B = logA + logB,所以这里加上log(pClass1)
p1 = sum(vec2Classify * p1Vec) + np.log(pClass1) #vec2Classify内是0,1,相乘后没有的就置0了,没影响
p0 = sum(vec2Classify * p0Vec)+ np.log(1.0 - pClass1)
print('p0:', p0)
print('p1:', p1)
if p1 > p0: #侮辱类概率大于非侮辱的,返回1,侮辱类
return 1
else:
return 0
使⽤NumPy的数组来计算两个向量相乘的结果。这⾥的相乘是指对应元素相乘,即先将两个向 量中的第1个元素相乘,然后将第2个元素相乘,以此类推。接下来将词汇表中所有词的对应值相加(对数下的加是普通情况下的乘),然后将该值加到类别的对数概率上。最后,⽐较类别的概率返回⼤概率对应的类别标签。
5. 测试朴素贝叶斯
def testingNB():
listOPosts,listClasses = loadDataSet() #创建实验样本
myVocabList = createVocabList(listOPosts) #创建词汇表
trainMat=[]
for postinDoc in listOPosts:
trainMat.append(setOfWords2Vec(myVocabList, postinDoc)) #将实验样本向量化
p0V,p1V,pAb = trainNB0(np.array(trainMat),np.array(listClasses)) #训练朴素贝叶斯分类器
testEntry = ['love', 'my', 'dalmation'] #测试样本1
thisDoc = np.array(setOfWords2Vec(myVocabList, testEntry)) #测试样本向量化
if classifyNB(thisDoc,p0V,p1V,pAb):
print(testEntry,'属于侮辱类') #执行分类并打印分类结果
else:
print(testEntry,'属于非侮辱类') #执行分类并打印分类结果
testEntry = ['stupid', 'garbage'] #测试样本2
thisDoc = np.array(setOfWords2Vec(myVocabList, testEntry)) #测试样本向量化
#print('b',thisDoc)
if classifyNB(thisDoc,p0V,p1V,pAb):
print(testEntry,'属于侮辱类') #执行分类并打印分类结果
else:
print(testEntry,'属于非侮辱类') #执行分类并打印分类结果
#------------测试-----------------------------
#测试
if __name__ == '__main__':
testingNB()
结果:
['love', 'my', 'dalmation'] 属于非侮辱类
['stupid', 'garbage'] 属于侮辱类
好了,一个简单的贝叶斯分类器完成了,下面就是实际应用,我们要怎么用呢?
四、 实例—垃圾邮件的过滤
在前面那个简单的例⼦中,我们引⼊了字符串列表。 使用朴素贝叶斯解决⼀些现实⽣活中的问题时,需要先从⽂本内容得到字符串列表,然后⽣成词向量。下面这个例⼦中,我们将了解朴素贝叶斯的⼀个最著名的应⽤:电⼦邮件垃圾过滤。首先看⼀下如何使⽤通用框架来解决该问题。
使⽤朴素贝叶斯对电⼦邮件进⾏分类流程
- 收集数据:置顶资料下载处自行下载。
- 准备数据:将文本文件解析成词条向量。
- 分析数据:检查词条确保解析的正确性。
- 训练算法:使用我们之前建立的trainNB0()函数。
- 测试算法:使⽤classifyNB(),并且构建⼀个新的测试函数来计算文档集的错误率。
- 使⽤算法:构建⼀个完整的程序对⼀组⽂档进行分类,将错分的文档输出到屏幕上。
收集部分已经完成,下面就在准备数据开始吧!
1. 准备数据:切分文本
前⼀节介绍了如何创建词向量,并基于这些词向量进行朴素贝叶斯分类的过程。前⼀节中的词向量是预先给定的,下⾯介绍如何从⽂本⽂档中构建自己的词列表。
首先导入相关包
"""
@Author:Yuuuuu、Tian
Wed Feb 19 09:02:16 2020
"""
import re #正则表达式模块
import numpy as np
import random
接下来,准备数据,构建自己的词向量,接受字符串,转变成单词列表
def textParse(bigString): #将字符串转换为字符列表
listOfTokens = re.split(r'\W', bigString) #将特殊符号作为切分标志进行字符串切分,即非字母、非数字
return [tok.lower() for tok in listOfTokens if len(tok) > 2] #除了单个字母,例如大写的I,其它单词变成小写
# def textParse(bigString): #将字符串转换为字符列表
# listOfTokens = re.split(r'\W*',bigString) #将特殊符号作为切分标志进行字符串切分,即非字母、非数字
# toks = []
# for tok in listOfTokens:
# #print('a',tok)
# if len(tok) > 2: #除了单个字母,例如大写的I,其它单词变成小写
# tok.lower()
# toks.append(tok)
# return toks
#创建一个不重复的列表---词汇表
def createVocabList(dataSet):
vocabSet = set([])
for document in dataSet:
vocabSet = vocabSet|set(document)
return list(vocabSet)
写一个测试函数测试一下
#遍历文件
if __name__ == '__main__':
docList = []; classList = []
for i in range(1,26): #每类25个邮件
# 读取每个垃圾邮件,并字符串转换成字符串列表
wordList = textParse(open('0602 Dataset/email/spam/%d.txt'%i,'r').read())
print('ccc:',wordList)
docList.append(wordList)
#print('bb:',docList)
classList.append(1) #垃圾邮件标记为1
wordList = textParse(open('0602 Dataset/email/ham/%d.txt' %i, 'r').read())
docList.append(wordList)
classList.append(0) # 非垃圾邮件标记为0
vocabList = createVocabList(docList)
print(vocabList)
2. 文本向量化
得到了词汇表,接下来就是每个文本的向量化,和上个例子一样,不在赘述。
#文本向量化
def setOfWords2Vec(vocabList,inputSet):
returnVec = [0] * len(vocabList) #创建一个其中所含元素都为0的向量
for word in inputSet: #遍历每个词条
if word in vocabList: #如果词条存在于词汇表中,则置1
returnVec[vocabList.index(word)] = 1
else:
print("the word: %s is not in my Vocabulary!" % word)
return returnVec
3. 训练算法
训练算法也是和第一个例子中构造简单贝叶斯分类器中的训练算法相同,因为思路一样的,处理数据的格式也是一样的。
直接搬过来就可。不在赘述。
#训练函数
def trainNB0(trainMatrix,trainCategory):
"""
Parameters:
trainMatrix - 训练文档矩阵,即setOfWords2Vec返回的returnVec构成的矩阵
trainCategory - 训练类别标签向量,即loadDataSet返回的classVec
Returns:
p0Vect - 侮辱类的条件概率数组
p1Vect - 非侮辱类的条件概率数组
pAbusive - 文档属于侮辱类的概率
"""
#文档的数量
numtrainDocs = len(trainMatrix)
#每篇文档的词条数
numWords = len(trainMatrix[0])
#文档属于垃圾邮件的概率
pAbusive = sum(trainCategory) / float(numtrainDocs)
# 创建numpy.zeros数组,词条出现数初始化为0
#p0Num = np.zeros(numWords); p1Num = np.zeros(numWords)
p0Num = np.ones(numWords); p1Num = np.ones(numWords) #创建numpy.ones数组,词条出现数初始化为1,拉普拉斯平滑
p0Denom = 2.0; p1Denom = 2.0 #分母初始化为2,拉普拉斯平滑
for i in range(numtrainDocs):
#统计属于垃圾邮件的条件概率所需的数据,即P(w0|1),P(w1|1),P(w2|1)···
if trainCategory[i] == 1: # 统计属于垃圾邮件的条件概率所需的数据,即P(w0|1),P(w1|1),P(w2|1)···
p1Num += trainMatrix[i] #词条出现的次数统计
#print('aaa', p1Num)
p1Denom += sum(trainMatrix[i]) #垃圾邮件中单词总数
#print('bbb', p1Denom)
else: # 统计属于非垃圾邮件的条件概率所需的数据,即P(w0|0),P(w1|0),P(w2|0)···
p0Num += trainMatrix[i]
p0Denom += sum(trainMatrix[i])
p1Vect = np.log(p1Num / p1Denom)
p0Vect = np.log(p0Num / p0Denom) #取对数防止下溢
# print('aaa',p1Num)
# print('bbb',p1Denom)
return p0Vect,p1Vect,pAbusive
4. 分类函数
还是直接搬上个例子的,很简单有没有,因为通用的嘛ε=ε=ε=( ̄▽ ̄)
#分类函数
def classifyNB(vec2Classify,p0Vec,p1Vec,pClass1):
"""
Parameters:
vec2Classify - 待分类的词条数组
p0Vec - 垃圾邮件的条件概率数组
p1Vec - 非垃圾邮件的条件概率数组
pClass1 - 文档属于垃圾邮件的概率
Returns:
0 - 属于非垃圾邮件
1 - 属于侮垃圾邮件
"""
#reduce(lambda x, y: x * y, lst) lamda表达式,对lst里面的参数进行处理
# p1 = reduce(lambda x,y:x*y,vec2Classify * p1Vec) * pClass1 #对应元素相加
# p0 = reduce(lambda x,y: x*y,vec2Classify * p0Vec) * (1.0 - pClass1)
#对应拉普拉斯修正,因为取自然对数了。logab = loga + logb。
# 对应元素相乘。logA * B = logA + logB,所以这里加上log(pClass1)
p1 = sum(vec2Classify * p1Vec) + np.log(pClass1)
p0 = sum(vec2Classify * p0Vec)+ np.log(1.0 - pClass1)
# print('p0:', p0)
# print('p1:', p1)
if p1 > p0:
return 1
else:
return 0
5. 测试分类器
分类器训练完了,分类函数也写完了,接下来就是测试阶段了。
#测试朴素贝叶斯分类器
def spamTest():
docList = []
classList = []
fullText = []
for i in range(1,26):
wordList = textParse(open('0602 Dataset/email/spam/%d.txt'%i,'r').read()) #依次读垃圾邮件
docList.append(wordList)
fullText.append(wordList)
classList.append(1)
wordList = textParse(open('0602 Dataset/email/ham/%d.txt' % i, 'r').read()) # 依次读非垃圾邮件
docList.append(wordList)
fullText.append(wordList)
classList.append(0)
#单词去重,建立词汇表
vocabList = createVocabList(docList)
#开始训练,测试
#随机选10个作为测试集、
trainingSet = list(range(50)) #索引
testSet = []
for i in range(10): #选十个作为测试集
randIndex = int(random.uniform(0,len(trainingSet))) #在0到50间随机选择唯一数值
testSet.append(trainingSet[randIndex]) #添加测试集的索引值
del(trainingSet[randIndex]) #删除选出的测试集
#-------------------------------------------------------------
#测试集完成,剩下的为训练集
trainMat = [] #向量化,各文档在词汇表的情况
trainClass = []
for docIndex in trainingSet: #遍历训练集
reVec = setOfWords2Vec(vocabList,docList[docIndex]) #根据词汇表向量化
trainMat.append(reVec)
trainClass.append(classList[docIndex]) #邮件类型
#训练集数据处理完后,开始训练
p0V, p1V, pSpam = trainNB0(trainMat,trainClass)
#训练完毕
#查看正确率
#遍历使用分类器分类
errorCount = 0 # 错误个数
for docIndex in testSet:
#处理测试集数据--向量化
wordvector = setOfWords2Vec(vocabList,docList[docIndex])
#开始预测
result = classifyNB(wordvector, p0V, p1V, pSpam)
if result != classList[docIndex]:
errorCount += 1
print("分类错误的测试集:", docList[docIndex])
# print('c',errorCount)
# print('d',len(testSet))
errorrate = float(errorCount) / len(testSet) * 100
print("错误率为:%.2f%%" % errorrate)
#-------测试----------------------------------------
if __name__ == '__main__':
spamTest()
结果:
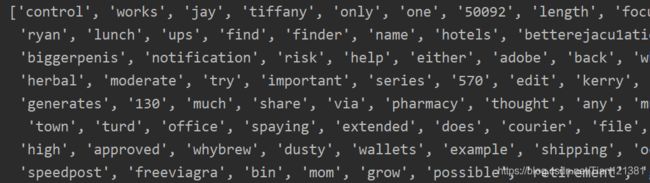
分类错误的测试集: ['home', 'based', 'business', 'opportunity', 'knocking', 'your', 'door', 'don抰', 'rude', 'and', 'let', 'this', 'chance', 'you', 'can', 'earn', 'great', 'income', 'and', 'find', 'your', 'financial', 'life', 'transformed', 'learn', 'more', 'here', 'your', 'success', 'work', 'from', 'home', 'finder', 'experts']
错误率为:10.00%
注:因为随机选择的训练集测试集,故错误率也不尽相同。
五 、 新闻分类(SKlearn)
背景:随着新闻量的逐渐增加,其分类也是让人头疼的问题,于是需要编写一个新闻分类的朴素贝叶斯分类器英文的语句可以通过非字母和非数字进行切分,但是汉语句子呢?这时候需要引入第三方的分词组件了‘jieba’可以直接安装。jieba具体教程
本例我们要用sklearn来构建朴素贝叶斯分类器。scikit-learn中朴素贝叶斯类库的使用也比较简单。相对于决策树,KNN之类的算法,朴素贝叶斯需要关注的参数是比较少的,这样也比较容易掌握。在scikit-learn中,一共有3个朴素贝叶斯的分类算法类。分别是GaussianNB,MultinomialNB和BernoulliNB。其中GaussianNB就是先验为高斯分布的朴素贝叶斯,MultinomialNB就是先验为多项式分布的朴素贝叶斯,
而BernoulliNB就是先验为伯努利分布的朴素贝叶斯。上篇文章讲解的先验概率模型就是先验概率为多项式分布的朴素贝叶斯。
对于新闻分类,属于多分类问题。我们可以使用MultinamialNB()完成我们的新闻分类问题。
MultinamialNB这个函数,只有3个参数:
- alpha:浮点型可选参数,默认为1.0,其实就是添加拉普拉斯平滑,即为上述公式中的λ ,如果这个参数设置为0,就是不添加平滑;
- fit_prior:布尔型可选参数,默认为True。布尔参数fit_prior表示是否要考虑先验概率, 如果是false,则所有的样本类别输出都有相同的类别先验概率。否则可以自己用第三个参数class_prior输入先验概率,或者不输入第三个参数class_prior让MultinomialNB自己从训练集样本来计算先验概率,此时的先验概率为P(Y=Ck)=mk/m。其中m为训练集样本总数量,mk为输出为第k类别的训练集样本数。
- class_prior:可选参数,默认为None
1. 处理数据
首先我们引入相关包
"""
@Author:Yuuuuu、Tian
Wed Feb 19 15:27:27 2020
"""
#导入相关包
from sklearn.naive_bayes import MultinomialNB
import matplotlib.pyplot as plt
import os
import random
import jieba
新闻可以分为很多类,我们用了不同的数字代码代替。将分类好的新闻放入了相应以这些数字代码命名的文件夹下。如下图
知道文件的结构了,那么就编写代码查看文件吧。
def TextProcessing(folder_path,test_size):
#查看folder_path下的文件
folder_list = os.listdir(folder_path) #查看folder_path下的文件
data_list = []
class_list =[]
for folder in folder_list: #遍历每个文件
new_folder_path = os.path.join(folder_path,folder) #路径拼接,生成新的路径
files = os.listdir(new_folder_path) #每个分类下的txt文件
#遍历每个txt文件
j = 1
for file in files:
if j > 100:
bread #每类样本最大100个
#读txt文件
raws = open(os.path.join(new_folder_path,file),'r',encoding='utf-8').read()
# with open(os.path.join(new_folder_path,file),'r',encoding='utf-8') as f:
# raws = f.read()
#通过jieba裁剪,详情https://www.cnblogs.com/aloiswei/p/11567616.html
word_cut = jieba.cut(raws,cut_all=False) #精简模式裁剪
word_list = list(word_cut) #转为列表
data_list.append(word_list) #加入数据列表
class_list.append(folder) #标题即类别
j += 1
# print(data_list)
# print(class_list)
#文本特征选择
#将所有文本划分为训练集和测试集,然后统计训练集中单词出现的频率,并按降序排列
#zip() 函数用于将可迭代的对象作为参数,将对象中对应的元素打包成一个个元组,然后返回由这些元组组成的列表。
data_class_list = list((zip(data_list,class_list))) #数据与对应标签合并压缩
random.shuffle(data_class_list) #打乱,好随机取
index = int(len(data_class_list) * test_size) + 1 #训练集测试集的划分点
train_list = data_class_list[index:] #index---最后为训练集
test_list = data_class_list[:index] #0---index-1为测试集
train_data_list,train_class_list = zip(*train_list) #解压缩
test_data_list,test_class_list = zip(*test_list)
#统计词频
all_words_dict = {} #创建空字典,为后续添加做准备
for word_list in train_data_list:
for word in word_list:
if word in all_words_dict:
all_words_dict[word] += 1
else:
all_words_dict[word] = 1
#根据键值倒序,大的放前面
all_words_tuple_dict = sorted(all_words_dict.items(),key=lambda f:f[1],reverse=True) #f[1]为值
all_words_list,all_words_num = zip(*all_words_tuple_dict) #解压缩 分开键,值
all_words_list = list(all_words_list) #转为列表
return all_words_list, train_data_list, test_data_list, train_class_list, test_class_list
#************测试***************************
if __name__ == '__main__':
# 文本预处理
folder_path = '0603 DataSet/SogouC/Sample' # 训练集存放地址
all_words_list, train_data_list, test_data_list, train_class_list, test_class_list = TextProcessing(folder_path, test_size=0.2)
print(all_words_list) #查看一下词出现多少的顺序
2. 分析数据
通过以上结果,可以看出,最多的是;‘的’,‘了’之类无关紧要的词,很显然,这些标点符号是不能作为新闻分类的特征的,所以要消除它们对分类结果的影响,首先去掉高频词,至于去掉多少个高频词,我们可以通过观察去掉高频词个数和最终检测准确率的关系来确定。除此之外,去除数字,不把数字作为分类特征。同时,去除一些特定的词语,比如:”的”,”一”,”在”,”不”,”当然”,”怎么”这类的对新闻分类无影响的介词、代词、连词。怎么去除这些词呢?可以使用已经整理好的stopwords_cn.txt文本(自备的无影响集)。可以根据这个文档,将这些单词去除,不作为分类的特征。我们先去除前100个高频词汇。
读取文件里的内容,并去重
def MakeWordsSet(word_file):
word_set = set()
with open(word_file,'r',encoding='utf-8') as f:
for line in f.readlines(): #一行行读
word = line.strip() #去回车
if len(word) > 0: #如果有文本,则添加
word_set.add(word)
return word_set
def TextFeatures(train_data_list, test_data_list, feature_words):
def text_features(text, feature_words): #出现在特征集中,则置1
text_words = set(text)
features = [1 if word in text_words else 0 for word in feature_words]
return features
train_feature_list = [text_features(text, feature_words) for text in train_data_list]
test_feature_list = [text_features(text, feature_words) for text in test_data_list]
return train_feature_list, test_feature_list #返回结果
#选取文本特征
def words_dict(all_words_list, deleteN, stopwords_set = set()):
"""
Parameters:
all_words_list - 训练集所有文本列表
deleteN - 删除词频最高的deleteN个词
stopwords_set - 自备的无影响集
Returns:
feature_words - 特征集
"""
feature_word = [] #特征列表
n = 1
# range(start, stop[, step]) #删除了频率最高的前N个
for i in range(deleteN,len(all_words_list),1): #跳过就等于删了
if n > 1000: #设特征值最大为1000
break
# 如果这个词不是数字,并且不是指定的自备的无影响集,并且单词长度大于1小于5,那么这个词就可以作为特征词
if not all_words_list[i].isdigit() and all_words_list[i] not in stopwords_set and 1 < len(all_words_list[i]) < 5:
feature_word.append(all_words_list[i])
n += 1
return feature_word
#-------------测试--------------------------------
if __name__ == '__main__':
#文本预处理
folder_path = '0603 DataSet/SogouC/Sample' #训练集存放地址
#返回全部数据集,训练集,测试集,训练集标签,测试集标签
all_words_list, train_data_list, test_data_list, train_class_list, test_class_list = TextProcessing(folder_path, test_size=0.2)
#生成stopwords_set
stopwords_file = '0603 DataSet/stopwords_cn.txt'
stopwords_set = MakeWordsSet(stopwords_file)
#删除前100个高频词
feature_words = words_dict(all_words_list, 100, stopwords_set)
print(feature_words)
结果:
['作战', '目前', '成为', '黄金周', '仿制', '学校', '五一', '问题', '比赛', '主要', '远程', '上海', '增长', '选择', '射程', '完全', '亿美元', '通过', '可能', '记者', '分析', '电话', '支付', '部署', '专业', '辅导班', '很多', '企业', '期间', '填报', '开始', '时候', '今年', '文章', '表示', '学习', '现在', '情况', '使用', '一定', 'VS', '复习', '工作', '表现', '专家', '阵地', '希望', '拥有', '部分', '用户', '资料', '相对', '坦克', '项目', '需要', '相关', '产品', '影响', '考试', '国家', '重要', '几乎', '比较', '这是', '基础', '管理', '发展', '达到', '能力', '网络', '服务', '历史', '军事', '日本', '万人次', '印度', '东莞', '来源', '老师', '考古', '一直', '数字', '显示', '必须', '准备', '技术', '发现', '专利', '彻底', '公里', '不用', '压制', '考研', '参加', '活动', '一次', '去年', '角度', '介绍', '非常', '收入', '要求', '岛屿', '大批', '阿里', '实验室', '训练', '游戏', '耿大勇', '告诉', '休闲', '人数', '接待', '知道', '最后', '全国', '作用', '距离', '沿海', '摧毁', '孩子', '睡眠', '一家', '方式', '机会', '提供', '协议', '挑衅', '置于', '应该', '数独', '系统', '提高', '计划', '成功', '世界', '越来越', '全球', '平台', '我国', '新型', '设计', '台湾', '自寻死路', '世界领先', '型号', '开战', '金贵', '海量', '之内', '费多', '力气', '廉价', '纳斯', '建议', '指挥', '目标', '装备', '这种', '消费者', '文化', '经济', '吸引', '看到', '增加', '了解', '两个', '完成', '获得', '不能', '进入', '重点', '不同', '医院', '药厂', '决定', '牛奶', 'MBA', '沈阳市', '左右', '喜欢', '最大', '出现', '包括', '手机', '一批', '未来', '大学生', '网上', '广东', '此前', '止痛药', '武器', '治疗', '预期', '东引岛', '今天', '战场', '录取', '方面', '消费', '东南亚', '第一次', '国内', '能够', '这家', '价值', '考虑', '复试', '是否', '推出', '理由', '排名', '教育', '数学', '分期付款', '利用', '实现', '英语', '设立', '小时', '交易', '第一', '过程', '明显', '事情', '镇痛药', '药物', '电脑', '赔偿', '之后', '原因', '结果', '营养', '本场', '辽宁队', '报道', '特别', '泰国', '代表', '俄罗斯', '埃及', '景区', '图库', '地方', '上市', '知名', '支持', '患者', '销售', '组织', '医疗', '中心', '詹姆斯', '著名', '对手', '同比', '建设', '学员', '演练', '消息', '院校', '分钟', '王治郅', '写作', '词汇', '认证', '公布', '旅游者', '全面', '旅行社', '指出', '不少', '一样', '最近', '媒体', '生活', '之前', '功能', '不会', '掌握', '之间', '简历', '很快', '根本', '研究', '正在', '内容', '上午', '火力', '各型', '补充', '当时', '帮助', '回家', '三个', '每个', '连续', '蓝军', '免息', '预计', '韩国', '商机', '欧洲', '城市', '感到', '关国光', '品牌', '容易', '分公司', '面试', '社会', '疼痛', '国际', '伯德', '姚明', '我省', '过年', '不要', '一下', '职业', '备考', '经验', '大学', '实施', '得到', '旅游业', '价格', '因素', '变得', '协会', '安排', '一位', '感觉', '发布', '数量', '过去', '开通', '有限公司', '女士', '提前', '关注', '环境', '采取', '努力', '这次', '本报', '共同', '其实', '参与', '网站', '一场', '找到', '整个', '意味着', '文物', '南京', '口技', '市民', '运动', '注意', '失眠', '战斗', '标题', '电视', '下载', '密码', '批次', '本科', '教材', '阅读', '评选', '遗址', '晋升', 'H股', '股东', '元老', '宣布', '合作', '预测', '出境', '公民', '景点', '数据', '不再', '法国', '发生', '大量', '这一', '条件', '最佳', '十分', '统计', '一起', '广播', '刚刚', '客户', '银行', '形成', '状态', '相当', '骗局', '人才', '制药', '先后', '更加', '第二', '压力', '每股', '邮票', '具有', '攻击', '胜利', '昨天', '每天', 'gt', '同事', '同学', '吸收', '家长', '关键字', '美国在线', '东部', '内容摘要', '补报', '关系', '升旗', '听课', '规则', '新浪', '信息', '透露', '结束', '超过', '基本', '展开', '月份', '资源', '创造', '一年', '香港', '只能', '一半', '面对', '举行', '万人', '购买', '本报记者', '方向', '之一', '效果', '电子', '领域', '跨国公司', '总部', '培训', '有点', '搜索', '不断', '销售额', '迅速', '阿片类', '产生', '困难', '多年', '诉讼', '主动', '失去', '本书', '有效', '米勒', '三分', '罚球', 'NBA', '以下', '十大', '感受', '充足', '人体', '办法', '场位', '红军', '知识', '可选报', '俱乐部', '工程', '辽足', '马林', '唐尧东', '导演', '敏华', '吸烟', '戒烟', '埃弗顿', '沈阳', '口语', '牙膏', '初盘', '围棋', '海上', '进一步', '模拟', '熟悉', '负责人', '标志', '往往', '航线', '专门', '东北亚', '回到', '有望', '费用', '机构', '带来', '几天', '时代', '平均', '年前', '负责', '举办', '广告', '留下', '挑战', '工具', '特点', '业务', '安全性', '保证', '核心', '应用', '稳定', '取得', '招聘', '提醒', '半导体', '人士', '继续', '提升', '年代', '万元', '发挥', '下降', '力量', '泰华', '收益', '大师', '地点', '加强', '短程', '战术导弹', '点穴', '现场', '真的', '经典', '关键', '真正', '实力', '最终', '亿元', '领导', '投诉', '乡村', '方法', '机票', '避免', '身高', '生长', '晚上', '最好', '几个', '很大', '意义', '呼叫', '业绩', '去年同期', '高清晰', '装甲团', '一页', '优秀', '兵器', '国旗', '理解', '学生', '标准', '语法', '辅导', '成绩', '研究所', '考场', '听力', '安妮', '汪力', '家教', '女兵', '连队', '日电', '即将', '双方', '相互', '地位', '突破', '出境游', '赢得', '旅游圈', '促进', '修改', '总数', '速度', '几年', '主题', '心理', '来到', '一般', '尤其', '春节', '正式', '变成', '巨大', '提出', '商店', '人口', '相比', '垃圾', '经理', '直接', '采用', '意外', '原则', '独立', '行业', '发出', '工资', '广州', '非甾体', '引起', '依然', '事件', '导致', '比例', '吗啡', '突出', '批准', '高达', '开展', '签订', '类似', '涉及', '难度', '生物', '增幅', '市营率', '起来', 'www', '公斤', '造成', '军方', '不足', '外界', '战术', '进攻', '精神', '团队', '表演', '股骨头', '不好', '兄弟', '仍然', '荷兰', '入睡', '食物', '听到', '表明', '主队', '学院', '战争', '综合', '命令', '练习', '英文', '故障', '华纳', 'BBC', '免费', '安契塔', '招生', '调剂', '各地', '坚持', '季泽', '想起', '考前', '必要', '参考书', '题目', '参看', '二外', '雅思', '已有', '陈祖德', '首次', '迎来', '地区', '固定', '部门', '水平', '普吉岛', '目的地', '无疑', '拉动']
运行后,可以看到,已经滤除了那些没有用的词组,这个feature_words就是我们最终选出的用于新闻分类的特征。随后,我们就可以根据feature_words,将文本向量化,然后用于训练朴素贝叶斯分类器。这个向量化的思想和前面的思想一致,因此不再累述。
3. sklearn构造贝叶斯分类器
由上所说我们将要使用 MultinomialNB分类算法类。MultinomialNB一个重要的功能是有partial_fit方法,这个方法的一般用在如果训练集数据量非常大,一次不能全部载入内存的时候。这时我们可以把训练集分成若干等分,重复调用partial_fit来一步步的学习训练集,非常方便。代码也很简单,如下
def TextClassifier(train_feature_list, test_feature_list, train_class_list, test_class_list):
classifier = MultinomialNB().fit(train_feature_list, train_class_list) #拟合训练集及其标签
test_accuracy = classifier.score(test_feature_list, test_class_list) #使用测试集测试结果
return test_accuracy
4. 参数调试
上面,我们默认的是删除前100个高频词,那我们又这么知道比100大或比100小的情况下,准确率不会更高呢?这节我们就来直观的解决下这个问题。直观看出问题所在当然就是画图了。
我们就依次删除前20,40,60,…1000个高频词,看看谁的准确率最高吧!
if __name__ == '__main__':
#文本预处理
folder_path = '0603 DataSet/SogouC/Sample' #训练集存放地址
all_words_list, train_data_list, test_data_list, train_class_list, test_class_list = TextProcessing(folder_path, test_size=0.2)
# 生成stopwords_set
stopwords_file = '0603 DataSet/stopwords_cn.txt'
stopwords_set = MakeWordsSet(stopwords_file)
test_accuracy_list = []
deleteNs = range(0, 1000, 20) #依次0 20 40 60 ... 980
for deleteN in deleteNs:
feature_words = words_dict(all_words_list, deleteN, stopwords_set)
train_feature_list, test_feature_list = TextFeatures(train_data_list, test_data_list, feature_words)
test_accuracy = TextClassifier(train_feature_list, test_feature_list, train_class_list, test_class_list)
test_accuracy_list.append(test_accuracy) #准确度列表
plt.figure()
plt.plot(deleteNs, test_accuracy_list)
plt.title('Relationship of deleteNs and test_accuracy')
plt.xlabel('deleteNs')
plt.ylabel('test_accuracy')
plt.show()
结果:

可以清晰的看出删除前450个高频词,准确率是最高的。(随机取得测试集,训练集,图不一定一样,多试几次,看在哪的几率高)
5. 使用分类器
那么最后就通过我们知道的参数运行一下吧!
#运行
if __name__ == '__main__':
#文本预处理
folder_path = '0603 DataSet/SogouC/Sample' #训练集存放地址
all_words_list, train_data_list, test_data_list, train_class_list, test_class_list = TextProcessing(folder_path, test_size=0.2)
# 生成stopwords_set
stopwords_file = '0603 DataSet/stopwords_cn.txt'
stopwords_set = MakeWordsSet(stopwords_file)
test_accuracy_list = []
feature_words = words_dict(all_words_list, 450, stopwords_set)
train_feature_list, test_feature_list = TextFeatures(train_data_list, test_data_list, feature_words)
test_accuracy = TextClassifier(train_feature_list, test_feature_list, train_class_list, test_class_list)
test_accuracy_list.append(test_accuracy)
ave = lambda c: sum(c) / len(c)
print(ave(test_accuracy_list)) #查看一下450情况下的正确率
结果:
0.7368421052631579
这节的内容就到此结束啦啦啦啦(。・∀・)ノ
六 、 总结
对于分类而言,使⽤概率有时要⽐使⽤硬规则更为有效。贝叶斯概率及贝叶斯准则提供了⼀种利用已知值来估计未知概率的有效⽅法。 可以通过特征之间的条件独立性假设,降低对数据量的需求。独⽴性假设是指⼀个词的出现概率并不依赖于文档中的其他词。当然我们也知道这个假设过于简单。这就是之所以称为朴素贝叶斯的原因。尽管条件独立性假设并不正确,但是朴素贝叶斯仍然是⼀种有效的分类器。
利⽤现代编程语⾔来实现朴素贝叶斯时需要考虑很多实际因素。下溢出就是其中⼀个问题,它可以通过对概率取对数来解决。还有其他⼀些方面的改进,比如说移除停用词,当然也可以花⼤量时间对切分器进行优化。 本章学习到的概率理论将在后续章节中⽤到,另外本章也给出了有关贝叶斯概率理论全⾯具体的介绍。接下来的⼀章将暂时不再讨论概率理论这⼀话题,介绍另⼀种称作Logistic回归的分类⽅法及⼀些优化算法。下章见(~ ̄▽ ̄)~
- 本文结合各位大牛所思所想,不胜感激!
- 如有错误,请不吝指正!
- 喜欢的请点赞呀(★ ω ★)