人工智能基础部分4-梯度下降和反向传播
大家好,我是微学AI,今天给大家讲一下梯度下降和反向传播的概念。
一、梯度下降法:
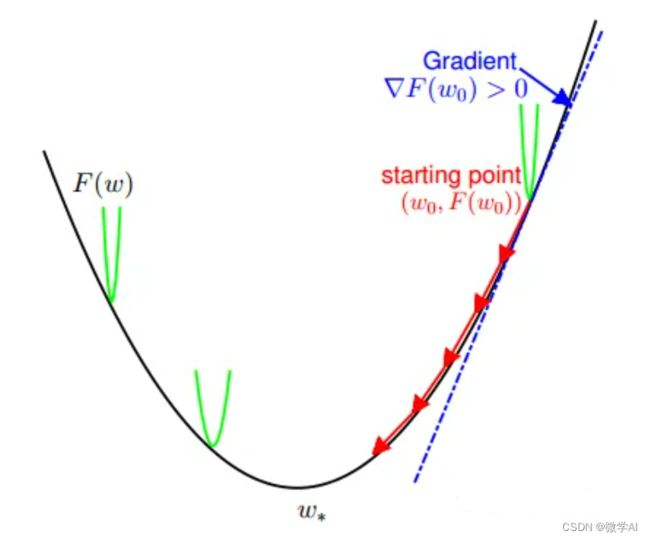
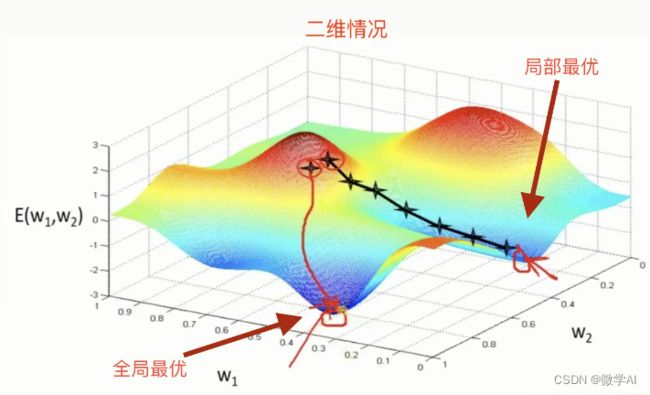
梯度下降(Gradient Descent)是一种最优化算法,用于求解最小化损失函数的参数值。梯度下降的基本思想是:根据当前参数的梯度,沿着梯度的反方向移动参数,从而找到损失函数的最小值。梯度下降在机器学习和深度学习中被广泛应用,用于优化模型参数。
梯度下降的原理可以用简单的话来概括:在一个高维空间中,梯度下降就是从一个点出发,根据损失函数的导数,沿着损失函数下降最快的方向,一步步朝着最优解前进,最终到达最优解处。
举个生动的例子:
想象一个人在爬山,需要到达山顶,而他所在的位置却在山脚下,他需要不断前进才能到达山顶。我们把山顶看做反向过来的损失函数的最小值,而山脚下则是损失函数的初始值,每次前进就相当于梯度下降中的一次迭代,人会根据山体的坡度不断调整自己的行进方向,朝着山顶的方向前进,最终到达山顶。
二、反向传播:
反向传播(Backpropagation)是一种形式化的梯度下降算法,用于训练神经网络。反向传播的基本思想是:用输出层的梯度反向传播到隐藏层,以计算每一层的梯度,并将梯度更新到参数,以期望找到损失函数的最小值。反向传播结合了梯度下降算法和负梯度方向的求解。
反向传播的原理是:在神经网络的输出层向输入层依次反向传播误差,在每层计算误差对每个参数的偏导,并通过梯度下降法更新权重参数,以期望最小化误差,从而提高模型的准确性。具体而言,它有以下几个步骤:
1. 将训练数据输入到神经网络,并计算输出;
2. 计算输出层的误差;
3. 将误差反向传播到每一层,并计算每一层的误差对每个参数的偏导;
4. 更新参数,使误差最小化;
5. 重复执行上述步骤,直到模型训练完毕。
反向传播就像一个探索迷宫的小朋友,反向传播就是从迷宫的出口开始,一步一步回溯,找到最初进入迷宫的位置,也就是迷宫的入口。在深度学习中,反向传播的过程就是从输出层开始,回溯将每一层的误差反向传播到输入层,从而更新权重,以最小化误差。
三、代码实战:
1、梯度下降案例:
# 构造数据
x_data = [1.0, 2.0, 3.0]
y_data = [2.0, 4.0, 6.0]
# 模型参数
w = 1.0 # 初始化w
# 模型定义
def forward(x):
return x * w
# 损失函数
def loss(x, y):
y_pred = forward(x)
return (y_pred - y) ** 2
# 梯度
def gradient(x, y): # d_loss/d_w
return 2 * x * (x * w - y)
# 更新参数
def update():
global w
w = w - 0.01 * gradient(x_data[0], y_data[0])
# 打印结果
for epoch in range(100):
for x_val, y_val in zip(x_data, y_data):
grad = gradient(x_val, y_val)
w = w - 0.01 * grad
print("\tgrad: ", x_val, y_val, round(grad, 2))
l = loss(x_val, y_val)
print("progress:", epoch, "w=", round(w, 2), "loss=", round(l, 2))2、方向传播(pytorch 框架简单案例):
import torch
# 定义一个简单的线性模型
model = torch.nn.Linear(1, 1)
# 定义优化器
optimizer = torch.optim.SGD(model.parameters(), lr=0.01)
# 定义损失函数
criterion = torch.nn.MSELoss()
# 训练数据
x_data = torch.tensor([[1.0], [2.0], [3.0]])
y_data = torch.tensor([[2.0], [4.0], [6.0]])
# 训练模型
for epoch in range(1000):
# 计算模型输出
y_pred = model(x_data)
# 计算损失
loss = criterion(y_pred, y_data)
# 清空梯度
optimizer.zero_grad()
# 反向传播
loss.backward()
# 更新参数
optimizer.step()
# 打印训练结果
if (epoch+1) % 20 == 0:
print(f'epoch {epoch+1}: w = {model.weight.item():.3f}, loss = {loss.item():.8f}')
# 训练完成
w = model.weight.item()
print(f'Predict after training: f(5) = {5*w:.3f}')
#模型保存
torch.save(model.state_dict(), 'model.pth')
#模型加载
state_dict = torch.load('model.pth')
model.load_state_dict(state_dict )
#模型预测
predict = model(torch.tensor([5.0]))
print(predict.detach().numpy()[0])运行结果
...
epoch 820: w = 1.948, loss = 0.00200677
epoch 840: w = 1.951, loss = 0.00182258
epoch 860: w = 1.953, loss = 0.00165529
epoch 880: w = 1.955, loss = 0.00150337
epoch 900: w = 1.957, loss = 0.00136538
epoch 920: w = 1.959, loss = 0.00124005
epoch 940: w = 1.961, loss = 0.00112624
epoch 960: w = 1.963, loss = 0.00102287
epoch 980: w = 1.965, loss = 0.00092898
epoch 1000: w = 1.966, loss = 0.00084371
9.908231
Predict after training: f(5) = 9.832以上简述了pytorch框架下训练线性模型的过程,清晰地描述了pytorch框架下模型训练的步骤,包括模型保存,模型加载,模型预测,全流程,掌握这个过程相当于pytorch框架学习了主心骨部分,大家可以尝试训练的过程。
有任何技术问题,可以私聊沟通!