Python sklearn针对不同人群的差异化保险费用定价方案

一、背景

传统健康险产品需要依靠“生命表”和“重大疾病发生率表”来进行产品设计。不同保险公司在设计产品时都需要基于以上两表，这就导致保险产品的同质化日益加重。同时由于传统的健康险产品基于总体发生概率来确定风险杠杆，吸烟体人群和非吸烟体人群的个体化差异被忽视。 使用机器学习技术，可以训练出针对个体的风险判断模型，通过该模型来估算不同个体的风险杠杆，以实现吸烟体和非吸烟体人群保险费率差异化定价。

二、样本数据分析

1、训练集数据

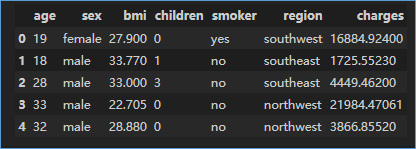
共计1338条美国地区被保险人数据，每条数据包括年龄、性别、BMI指数、子女数、是否吸烟、所属地区、保费。
数据集下载链接：https://www.kaggle.com/teertha/ushealthinsurancedataset

#导入数据集
import pandas as pd
data=pd.read_csv('insurance.csv')
data.head()

• 样本中维度数据包括：性别（sex）、是否吸烟体（smoker）、地区（region）；
• 样本中数值数据包括：年龄（age）、身体质量指数（BMI）、抚养孩子数量（children）、保费（charge）;
• 样本中男性占比50.5%，女性占比49.5%；
• 样本平均年龄39.2岁，其中最小18岁，最大64岁；
• 样本BMI平均指数为30.66 (WHO推荐的判断标准为：BMI<18.5为消瘦，18.5～24.9为正常，25～29.9为超重，≥30为肥胖);
• 样本中20.5%的交保者为吸烟体；

2、数据分析

从性别（sex）、是否吸烟体（smoker）、地区（region）、年龄（age）、身体质量指数（BMI）、抚养孩子数量（children）角度出发分析不同投保人群的保费差异以及产生保费差异的外部及内部原因。

2.1不同性别保险费分析

2.1.1男女保险费分布情况

#男女保费箱线图
import matplotlib.pyplot as plt
import seaborn as sns
sns.set_style('darkgrid', {'font.sans-serif':['SimHei', 'Arial']})#设置图表背景颜色字体
sns.boxplot(y='charges',data=data,x='sex',order=['male','female'],palette='Set3',saturation=1.5,fliersize=4,notch=True)
plt.title('男女保费分布箱线图')

• 男性相比较于女性保费分布更广，意味着样本中更多的男性保费高于女性保费；

2.1.2导致男女保费不同的原因

(1)分析年龄和BMI对男女保费的影响

#不同性别年龄和bmi核密度图
cols = ['age','bmi']
sex = ['female','male']
fig,ax = plt.subplots(1,2,figsize=(12,4))
for col,p in zip(cols,range(2)):
    for s in sex:
        sns.kdeplot(data[col][data['sex']==s],label=s,ax=ax[p],shade=True)
        ax[p].set_title('不同性别%s分布特征'%col)
        ax[p].legend()

• 样本中不同性别的年龄和BMI差异不大，未表现出显著性差异，所以并非年龄和BMI导致男女保费不同；

(2)分析抚养孩子数量对男女保费的影响

#不同性别抚养孩子数量柱状图
sns.countplot(data=data,x='children',hue='sex')
plt.title('不同性别抚养孩子数量比较')

• 样本中并未表现出男女在抚养孩子数量方面的差异，所以并非孩子数量不同导致男女保费不同；

(3)分析是否吸烟对男女保费的影响

#不同性别吸烟体和非吸烟体保费分布箱线图
sns.boxplot(y='charges',data=data,x='sex',hue='smoker',order=['male','female'],palette='Set3',saturation=1.5,fliersize=4,notch=True)
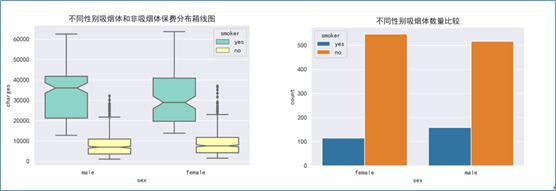
plt.title('不同性别吸烟体和非吸烟体保费分布箱线图')

#不同性别吸烟体数量比较柱状图
sns.countplot(data=data,x='sex',hue='smoker')
plt.title('不同性别吸烟体数量比较')

• 无论是男性还是女性，吸烟体的保费分布远远高于非吸烟体的保费分布，意味着样本中更多的吸烟体投保者保费高于非吸烟体投保者；
• 男性吸烟人数略大于男性吸烟人数；
• 可见吸烟是导致男性高保费的重要因素之一；

(4)分析结果

由以上分析得出，导致男女保费存在差异的主要因素为是否是吸烟体。

2.2吸烟体人群分析

在2.1中我们分析得到吸烟是导致男性高保费的重要因素之一。在2.2中我们进一步分析吸烟体人群与非吸烟体人群除保费不同之外的其他差异。

2.2.1吸烟体与非吸烟体人群的年龄和BMI分析

#吸烟体和非吸烟体年龄和bmi核密度图
cols = ['age','bmi']
sex = ['yes','no']
fig,ax = plt.subplots(1,2,figsize=(12,4))
for col,p in zip(cols,range(2)):
    for s in sex:
        sns.kdeplot(data[col][data['smoker']==s],label=s,ax=ax[p],shade=True)
        ax[p].set_title('吸烟体与非吸烟体%s分布特征'%col)
        ax[p].legend()

• 样本中吸烟体与非吸烟体人群的BMI和年龄分布并未有显著性差异；

2.2.2吸烟体与非吸烟体人群抚养孩子数量比较

#吸烟体和非吸烟体抚养孩子数量柱状图
sns.countplot(data=data,x='children',hue='smoker')
plt.title('吸烟体与非吸烟体抚养孩子差异比较')

• 吸烟体人群与非吸烟体人群在抚养孩子方面存在显著差异，样本中吸烟体人群抚养孩子的比例较小；

2.2.3抚养孩子数量对保费的影响

2.2.2中我们发现吸烟体人群抚养孩子的比例较小，在2.2.3中我们进一步分析抚养孩子数量对保费的影响。

#不同抚养儿童数量投保人的保费分布箱线图
sns.boxplot(y='charges',data=data,x='children',palette='Set3',saturation=1.5,fliersize=4,notch=True)
plt.title('不同抚养儿童数量投保人的保费分布箱线图')

• 样本中投保人抚养孩子数量在2个以内时，保费会随着孩子数量的增加而增加，孩子数量大于两个后，保费会随着孩子数量的增加而减小，可见抚养孩子数量与保费存在一定的关联性关系；

2.2.4分析结果

由以上分析结果可知，吸烟体人群相比于非吸烟体人群抚养孩子的数量较少。

2.3不同地区投保人保险费分析

2.3.1不同地区保费分布情况

#不同地区投保人群保费分布箱线图
sns.boxplot(y='charges',data=data,x='region',palette='Set3',saturation=1.5,fliersize=4,notch=True)
plt.title('不同地区投保人群保费分布箱线图')

• Southeast地区的保费分布相比于其他三个地区的保费分布要更高，意味着该地区较多的投保人的保费更高；

2.3.2导致不同地区保费分布不同的原因分析

（1）分析BMI对不同地区投保人保费的影响

#不同地区投保人BMI指数散点图
sns.stripplot(data=data,x='region',y='bmi')
plt.title('不同地区投保人BMI指数散点图')

• Southeast地区的BMI指数高于其他地区，BMI指数分布较高导致肥胖率增加；
• 可见BMI指数是导致Southeast地区保费较高的主要原因之一；

（2）分析抚养孩子数量对不同地区投保人保费的影响

#不同地区投保人抚养孩子平均数量
data_tem=data.groupby('region')['children'].mean()
data_tem=data_tem.sort_values()
data_tem.plot(kind='bar',rot=360)
plt.title('不同地区投保人抚养孩子数量平均值')
plt.ylabel('孩子数量')

• 不同地区投保人抚养孩子的平均数量未见明显差异；

（3）分析是否是吸烟体对不同地区投保人保费的影响

#不同地区吸烟体与非吸烟体投保人数量比较柱状图
sns.countplot(x=data['region'],hue=data['smoker'])
plt.title('不同地区吸烟体与非吸烟体投保人数量比较')

• 样本中Southeast地区中投保人中吸烟体的人数最多，该地区的投保人更爱吸烟，导致保费更高；

（4）分析年龄对不同地区投保人保费的影响；

#不同地区投保人年龄分布散点图
sns.stripplot(data=data,x='region',y='age')
plt.title('不同地区投保人年龄分布散点图')

#不同地区投保人年龄平均值柱状图
reg_age=data.groupby('region')['age'].mean()
reg_age=reg_age.sort_values()
reg_age.plot(kind='bar',rot=360)
plt.title('不同地区投保人年龄平均值')
plt.ylabel('平均年龄')

• 样本中不同地区投保人的年龄分布和年龄平均值未见显著差异

2.3.3分析结果

以上分析得出，导致Southeas地区投保人群保费较高的主要因素是该地区投保人BMI指数偏高且投保人中吸烟体比例较高。

2.4BMI指数对投保人保费的影响

2.4.1吸烟体与非吸烟体的保费与BMI指数的关系

#BMI指数对投保人保费的影响线性回归图
plt.rcParams["font.size"]=12
sns.lmplot(data=data,x='bmi',y='charges',hue='smoker',line_kws=dict(color='black',alpha=0.6),scatter_kws=dict(alpha=0.6))
plt.fill_betweenx(x1=18.5,x2=30,y=(-100,69000),facecolor='gray',alpha=0.3,edgecolor='w')
plt.text(x=18.6,y=67000,s='18.5≤BMI<30',fontsize=10)
plt.title('BMI指数对投保人保费的影响',fontsize=10)

• 样本中吸烟体的保费普遍高于非吸烟体；
• 样本中非吸烟体的保费随着BMI指数的增长而缓慢增长，吸烟体的保费增长速度则显著高于非吸烟体，在BMI指数超过30后，即达到肥胖标准后，吸烟体的保费增长速度陡增；

2.4.2分析结果

BMI指数是投保人保费产生保费差异的重要因素之一，其中吸烟体投保人的保费与BMI指数的关联程度更大。

2.5年龄对投保人保费的影响

2.5.1吸烟体与非吸烟体的保费与年龄的关系

#年龄对投保人保费的影响线性回归图
plt.rcParams["font.size"]=12
sns.lmplot(data=data,x='age',y='charges',hue='smoker',line_kws=dict(color='black',alpha=0.6),scatter_kws=dict(alpha=0.6))
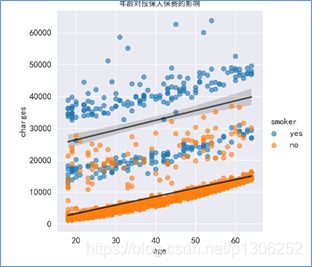
plt.title('年龄对投保人保费的影响',fontsize=10)

• 样本中吸烟体的保费普遍高于非吸烟体；
• 无论是吸烟体还是非吸烟体，年龄越大，保费越高；

2.5.2分析结果

年龄与保费存在一定的正相关性。

三、多元线性回归模型预测保险费

多元线性回归是由多个自变量的最优组合来共同预测或估计结果的数学模型。在对样本的分析中，我们已经得知是否吸烟体、年龄以及BMI三个变量构成了影响保费的三大要素。接下俩，我们以该样本数据为基础，创建并训练多元线性回归模型，将是否吸烟体、年龄以及BMI作为因变量来预测最终的保险费。
预测公式为：y=〖b_0+b〗_1 x_1+b_2 x_2+〖b_3 x〗_3。其中x_1为是否吸烟体变量，x_2为年龄变量，x_3为BMI指数变量。b_1、b_2、b_3为回归系数，b_0为常数项。
1、哑变量处理

catColumns = ['sex', 'smoker', 'region']
data_dum = pd.get_dummies(data, columns = catColumns, drop_first=True)

2、设置自变量x,因变量y

x = data_dum[['age','bmi', 'smoker_yes']]
y = data_dum['charges']

3、通过Python sklearn创建多元线性回归模型

from sklearn.linear_model import LinearRegression, RidgeCV, LassoCV
linreg = LinearRegression()#创建线性回归模型
ridgereg = RidgeCV(alphas=(0.1,0.3,0.7,1.0),cv=5)
lassoreg = LassoCV(eps=0.001, cv = 5)
from sklearn.model_selection import cross_val_score
linreg.fit(x,y) 
linreg.score(x,y) #得到R平方值

最终得到的R平方值为自变量决定系数，该值越小，自变量对因变量的影响越弱，反之亦然。本例中，通过回归模型得到的R平方值0.7474771588119513，即是否吸烟体、年龄、BMI影响保费74.7%，其余则受模型外其他变量的影响。
4、得到回归系数和常数值

linreg.coef_#回归系数
linreg.intercept_#截距

样本数据集创建的回归模型得到的回归系数和常数值分别为：
b_1:259.54749155 , b_2:322.61513282, b_3:23823.68449531,b_0-11676.830425187782。
5、用回归模型进行保费预测

def calc_insurance(age,bmi,smoking):
    y = ((age*linreg.coef_[0])+(bmi*linreg.coef_[1])+(smoking*linreg.coef_[2])-linreg.intercept_)
    return y
 print(calc_insurance(40, 35, 0))
 print(calc_insurance(40, 35, 1))

某40岁非吸烟体，bmi为35的投保者，该模型预测的保费为33350.25973593014元；而某40岁吸烟体，bmi为35的投保者，该模型预测的保费为57173.94423123897元。
4、多元线性回归模型预测效果判断
我们将样本中的数据分成两部分，一部分用于训练该模型以确定模型参数，另一部分用于测试该模型以判断该模型的预测效果是否达到预期。在本例中我们用30%的数据作为训练集，70%的数据用于测试集。得到的模型拟合效果如下所示：

from sklearn.model_selection import train_test_split,cross_val_score
xtrain,xtest,ytrain,ytest = train_test_split(data_dum[['age','bmi','smoker_yes']],data_dum['charges'],test_size=0.3)
y_lpre = linreg .predict(xtest)
sns.scatterplot(ytest,y_lpre,label='LinearRegression')
sns.lineplot(x=[0,50000],y=[0,50000],label='perfect',color='black')
plt.legend()

• 可见在保费小于20000的时候，模型预测效果较好，但是当保费大于20000后，模型预测的效果较差；

四、决策树模型预测保险费

决策树模型通过对训练样本的学习，并建立分类规则，然后依据分类规则，对新样本数据进行分类预测。
1、通过Python sklearn创建决策树模型

from sklearn.tree import DecisionTreeRegressor
dre = DecisionTreeRegressor(criterion='mse',splitter='best',random_state=20,max_depth=4)
dre.fit(x,y)

2、决策数模型预测效果判断

y_dpre = dre.predict(xtest)
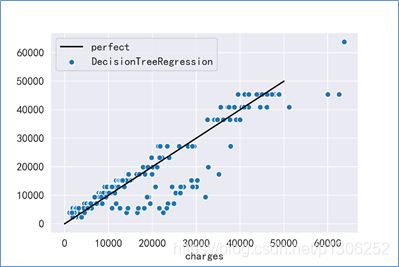
sns.scatterplot(ytest,y_dpre,label='DecisionTreeRegression')
sns.lineplot(x=[0,50000],y=[0,50000],label='perfect',color='black')
plt.legend()

• 可见在保费大于30000左右的时候，拟合预测效果较好，但是当保费小于30000后，模型预测的效果较差。

五、总结

通过对样本数据的分析，是否吸烟、年龄、BMI对保费的制定有着重要影响。我们以这三种变量分别取构建多元回归模型和决策树模型，发现保费较小时多元回归模型拟合度较好，而当保费较大时，决策树模型拟合度较好。
代码链接