图神经网络推荐方向--论文代码读记
前言
这篇作为自己读论文代码过程中一些简单的代码备忘读记吧,方便查阅。
一、torch.cat() 、torch.stack()
拼接张量:torch.cat() 、torch.stack()
- torch.cat(inputs, dimension=0) → Tensor
在给定维度上对输入的张量序列 seq 进行连接操作
举个例子:
>>> ``import` `torch``
>>> x ``=` `torch.randn(``2``, ``3``)``
>>> x``tensor([[``-``0.1997``, ``-``0.6900``, ``0.7039``],`` ``[ ``0.0268``, ``-``1.0140``, ``-``2.9764``]])``
>>> torch.cat((x, x, x), ``0``) ``
# 在 0 维(纵向)进行拼接``tensor([[``-``0.1997``, ``-``0.6900``, ``0.7039``],`` ``[ ``0.0268``, ``-``1.0140``, ``-``2.9764``],`` ``[``-``0.1997``, ``-``0.6900``, ``0.7039``],`` ``[ ``0.0268``, ``-``1.0140``, ``-``2.9764``],`` ``[``-``0.1997``, ``-``0.6900``, ``0.7039``],`` ``[ ``0.0268``, ``-``1.0140``, ``-``2.9764``]])``
>>> torch.cat((x, x, x), ``1``) ``
# 在 1 维(横向)进行拼接``tensor([[``-``0.1997``, ``-``0.6900``, ``0.7039``, ``-``0.1997``, ``-``0.6900``, ``0.7039``, ``-``0.1997``, ``-``0.6900``,`` ``0.7039``],`` ``[ ``0.0268``, ``-``1.0140``, ``-``2.9764``, ``0.0268``, ``-``1.0140``, ``-``2.9764``, ``0.0268``, ``-``1.0140``,`` ``-``2.9764``]])``
>>> y1 ``=` `torch.randn(``5``, ``3``, ``6``)``
>>> y2 ``=` `torch.randn(``5``, ``3``, ``6``)``
>>>> torch.cat([y1, y2], ``2``).size()``torch.Size([``5``, ``3``, ``12``])``
>>> torch.cat([y1, y2], ``1``).size()``torch.Size([``5``, ``6``, ``6``])
对于需要拼接的张量,维度数量必须相同,进行拼接的维度的尺寸可以不同,但是其它维度的尺寸必须相同。
- torch.stack(sequence, dim=0)
沿着一个新维度对输入张量序列进行连接。 序列中所有的张量都应该为相同形状
举个例子:
>>> x1 ``=` `torch.randn(``2``, ``3``)``
>>>> x2 ``=` `torch.randn(``2``, ``3``)``
>>>> torch.stack((x1, x2), ``0``).size() ``
># 在 0 维插入一个维度,进行区分拼接``torch.Size([``2``, ``2``, ``3``])``
>>>> torch.stack((x1, x2), ``1``).size() `
># 在 1 维插入一个维度,进行组合拼接``
>torch.Size([``2``, ``2``, ``3``])``
>>>> torch.stack((x1, x2), ``2``).size()``torch.Size([``2``, ``3``, ``2``])``
>>>> torch.stack((x1, x2), ``0``)``tensor([[[``-``0.3499``, ``-``0.6124``, ``1.4332``],`` ``[ ``0.1516``, ``-``1.5439``, ``-``0.1758``]],` ` ``[[``-``0.4678``, ``-``1.1430``, ``-``0.5279``],`` ``[``-``0.4917``, ``-``0.6504``, ``2.2512``]]])``>>> torch.stack((x1, x2), ``1``)``tensor([[[``-``0.3499``, ``-``0.6124``, ``1.4332``],`` ``[``-``0.4678``, ``-``1.1430``, ``-``0.5279``]],` ` ``[[ ``0.1516``, ``-``1.5439``, ``-``0.1758``],`` ``[``-``0.4917``, ``-``0.6504``, ``2.2512``]]])``
>>>> torch.stack((x1, x2), ``2``)``tensor([[[``-``0.3499``, ``-``0.4678``],`` ``[``-``0.6124``, ``-``1.1430``],`` ``[ ``1.4332``, ``-``0.5279``]],` ` ``[[ ``0.1516``, ``-``0.4917``],`` ``[``-``1.5439``, ``-``0.6504``],`` ``[``-``0.1758``, ``2.2512``]]])
把相同形状的张量合并,并根据提供的维度序列在相应位置插入维度,方法会根据位置来排列数据。代码中,根据第 0 维和第 1 维来进行合并时,虽然合并后的张量维度和尺寸相等,但是数据的位置并不是相同的。
二、 拆分张量:torch.split()、torch.chunk()
- torch.split(tensor, split_size, dim=0)
将输入张量分割成相等形状的 chunks(如果可分)。 如果沿指定维的张量形状大小不能被 split_size 整分, 则最后一个分块会小于其它分块。
举个例子:
>>> x ``=` `torch.randn(``3``, ``10``, ``6``)``>>> a, b, c ``=` `x.split(``1``, ``0``) ``# 在 0 维进行间隔维 1 的拆分``>>> a.size(), b.size(), c.size()``(torch.Size([``1``, ``10``, ``6``]), torch.Size([``1``, ``10``, ``6``]), torch.Size([``1``, ``10``, ``6``]))``>>> d, e ``=` `x.split(``2``, ``0``) ``# 在 0 维进行间隔维 2 的拆分``>>> d.size(), e.size()``(torch.Size([``2``, ``10``, ``6``]), torch.Size([``1``, ``10``, ``6``]))
把张量在 0 维度上以间隔 1 来拆分时,其中 x 在 0 维度上的尺寸为 3,就可以分成 3 份。
把张量在 0 维度上以间隔 2 来拆分时,只能分成 2 份,且只能把前面部分先以间隔 2 来拆分,后面不足 2 的部分就直接作为一个分块。
- torch.chunk(tensor, chunks, dim=0)
在给定维度(轴)上将输入张量进行分块儿
直接用上面的数据来举个例子:
>>> l, m, n ``=` `x.chunk(``3``, ``0``) ``# 在 0 维上拆分成 3 份``
>>>> l.size(), m.size(), n.size()``(torch.Size([``1``, ``10``, ``6``]), torch.Size([``1``, ``10``, ``6``]), torch.Size([``1``, ``10``, ``6``]))``
>>>> u, v ``=` `x.chunk(``2``, ``0``) ``# 在 0 维上拆分成 2 份``
>>>> u.size(), v.size()``(torch.Size([``2``, ``10``, ``6``]), torch.Size([``1``, ``10``, ``6``]))
把张量在 0 维度上拆分成 3 部分时,因为尺寸正好为 3,所以每个分块的间隔相等,都为 1。
把张量在 0 维度上拆分成 2 部分时,无法平均分配,以上面的结果来看,可以看成是,用 0 维度的尺寸除以需要拆分的份数,把余数作为最后一个分块的间隔大小,再把前面的分块以相同的间隔拆分。
在某一维度上拆分的份数不能比这一维度的尺寸大。
稀疏矩阵是指矩阵中的元素大部分是0的矩阵,事实上,实际问题中大规模矩阵基本上都是稀疏矩阵,很多稀疏度在90%甚至99%以上。因此我们需要有高效的稀疏矩阵存储格式。本文总结几种典型的格式:COO,CSR,DIA,ELL,HYB。
三、稀疏矩阵表示
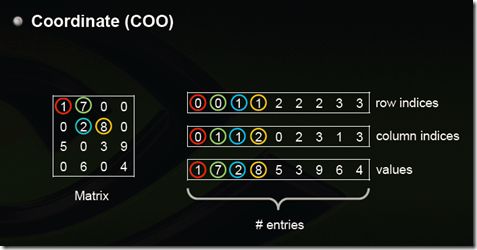
(1)Coordinate(COO)
这是最简单的一种格式,每一个元素需要用一个三元组来表示,分别是(行号,列号,数值),对应上图右边的一列。这种方式简单,但是记录单信息多(行列),每个三元组自己可以定位,因此空间不是最优。
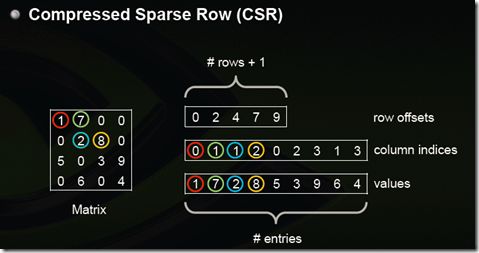
(2)Compressed Sparse Row (CSR)
CSR是比较标准的一种,也需要三类数据来表达:数值,列号,以及行偏移。CSR不是三元组,而是整体的编码方式。数值和列号与COO一致,表示一个元素以及其列号,行偏移表示某一行的第一个元素在values里面的起始偏移位置。如上图中,第一行元素1是0偏移,第二行元素2是2偏移,第三行元素5是4偏移,第4行元素6是7偏移。在行偏移的最后补上矩阵总的元素个数,本例中是9。
CSC是和CSR相对应的一种方式,即按列压缩的意思。
以上图中矩阵为例:
Values: [1 5 7 2 6 8 3 9 4]
Row Indices:[0 2 0 1 3 1 2 2 3]
Column Offsets:[0 2 5 7 9]
from scipy.sparse import *
row = [0,0,0,1,1,1,2,2,2]#行指标
col = [0,1,2,0,1,2,0,1,2]#列指标
data = [1,0,1,0,1,1,1,1,0]#在行指标列指标下的数字
team = csr_matrix((data,(row,col)),shape=(3,3))
print(team)
print(team.todense())
输出结果:
(0, 0) 1
(0, 1) 0
(0, 2) 1
(1, 0) 0
(1, 1) 1
(1, 2) 1
(2, 0) 1
(2, 1) 1
(2, 2) 0
[[1 0 1]
[0 1 1]
[1 1 0]]
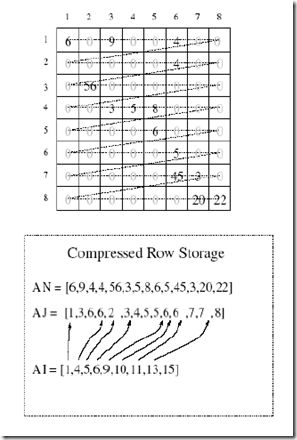
再来看一个CSR的例子[4]:
coo_matrix
coo_matrix是最简单的存储方式。采用三个数组row、col和data保存非零元素的信息。这三个数组的长度相同,row保存元素的行,col保存元素的列,data保存元素的值。一般来说,coo_matrix主要用来创建矩阵,因为coo_matrix无法对矩阵的元素进行增删改等操作,一旦矩阵创建成功以后,会转化为其他形式的矩阵。data = [5,2,3,0]
>>> row = [2,2,3,2]
>>> col = [3,4,2,3]
>>> c = sparse.coo_matrix((data,(row,col)),shape=(5,6))
>>> print c.toarray()
[[0 0 0 0 0 0]
[0 0 0 0 0 0]
[0 0 0 5 2 0]
[0 0 3 0 0 0]
[0 0 0 0 0 0]]
稍微需要注意的一点是,用coo_matrix创建矩阵的时候,相同的行列坐标可以出现多次。矩阵被真正创建完成以后,相应的坐标值会加起来得到最终的结果。
四、dok_matrix与lil_matrix
dok_matrix和lil_matrix适用的场景是逐渐添加矩阵的元素。
dok_matrix的策略是采用字典来记录矩阵中不为0的元素。自然,字典的key存的是记录元素的位置信息的元祖,value是记录元素的具体值。
>>> import numpy as np
>>> from scipy.sparse import dok_matrix
>>> S = dok_matrix((5, 5), dtype=np.float32)
>>> for i in range(5):
... for j in range(5):
... S[i, j] = i + j
...
>>> print S.toarray()
[[ 0. 1. 2. 3. 4.]
[ 1. 2. 3. 4. 5.]
[ 2. 3. 4. 5. 6.]
[ 3. 4. 5. 6. 7.]
[ 4. 5. 6. 7. 8.]]
lil_matrix则是使用两个列表存储非0元素。data保存每行中的非零元素,rows保存非零元素所在的列。这种格式也很适合逐个添加元素,并且能快速获取行相关的数据。
>>> from scipy.sparse import lil_matrix
>>> l = lil_matrix((6,5))
>>> l[2,3] = 1
>>> l[3,4] = 2
>>> l[3,2] = 3
>>> print l.toarray()
[[ 0. 0. 0. 0. 0.]
[ 0. 0. 0. 0. 0.]
[ 0. 0. 0. 1. 0.]
[ 0. 0. 3. 0. 2.]
[ 0. 0. 0. 0. 0.]
[ 0. 0. 0. 0. 0.]]
>>> print l.data
[[] [] [1.0] [3.0, 2.0] [] []]
>>> print l.rows
[[] [] [3] [2, 4] [] []]
五、dia_matrix
这是一种对角线的存储方式。其中,列代表对角线,行代表行。如果对角线上的元素全为0,则省略。
如果原始矩阵是个对角性很好的矩阵那压缩率会非常高。
找了网络上的一张图,大家就很容易能看明白其中的原理。
六、csr_matrix与csc_matrix
csr_matrix,全名为Compressed Sparse Row,是按行对矩阵进行压缩的。CSR需要三类数据:数值,列号,以及行偏移量。CSR是一种编码的方式,其中,数值与列号的含义,与coo里是一致的。行偏移表示某一行的第一个元素在values里面的起始偏移位置。
同样在网络上找了一张图,能比较好反映其中的原理。
以官方文档为例,此时data代表的是存储的值的数组,indices代表的是每一行中第几列有对应data中的元素,即从indices中可以推断出列的信息,
indptr则用来推断出行的信息,默认元素开始为0,第一个元素为2,则证明第一行中有2-0=2个元素,所以将data数组中前另个元素写入第一行中,而indices前两个元素为0,2,则代表第0列和第2列。前两第二个元素为3,证明第二行中有3-2=1个元素,该元素为data[2]=3,且存储在indices[2] = 2列中。依次类推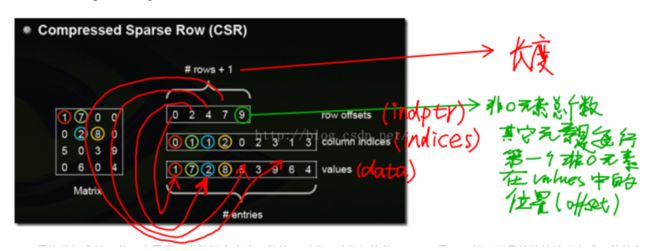
不难看出,csr_matrix比较适合用来做真正的矩阵运算。
至于csc_matrix,跟csr_matrix类似,只不过是基于列的方式压缩的,不再单独介绍。
七、bsr_matrix
按分块的思想对矩阵进行压缩。
八、tensorflow操作
tf.random_uniform
从均匀分布中输出随机值。
生成的值在该 [minval, maxval) 范围内遵循均匀分布.下限 minval 包含在范围内,而上限 maxval 被排除在外
tf.cast()函数的作用是执行 tensorflow 中张量数据类型转换,比如读入的图片如果是int8类型的,一般在要在训练前把图像的数据格式转换为float32。
tf.cast
cast定义:
cast(x, dtype, name=None)
第一个参数 x: 待转换的数据(张量)
第二个参数 dtype: 目标数据类型
第三个参数 name: 可选参数,定义操作的名称
tf.sparse_retain(X, dropout_mask)
在一个 SparseTensor 中保留指定的非空值.
例如,如果 sp_input 有形状 [4, 5] 和4个非空字符串值,如下所示:
[0, 1]: a
[0, 3]: b
[2, 0]: c
[3, 1]: d
并且 to_retain = [True, False, False, True],则输出将是一个形状为 [4, 5] 以及具有2个非空值的 SparseTensor:
[0, 1]: a
[3, 1]: d
函数参数:
- sp_input:输入的 SparseTensor 带有 N 个非空元素.
- to_retain:长度为 N 的具有 M 个真值的 bool 向量.
函数返回值:
该函数返回一个与输入具有相同形状并且有 M 个非空元素的 SparseTensor,它对应于 to_retain 的真实位置.
tf.matmul() 和tf.multiply() 的区别
1.tf.multiply()两个矩阵中对应元素各自相乘
格式: tf.multiply(x, y, name=None)
参数:
x: 一个类型为:half, float32, float64, uint8, int8, uint16, int16, int32, int64, complex64, complex128的张量。
y: 一个类型跟张量x相同的张量。
返回值: x * y element-wise.
注意:
(1)multiply这个函数实现的是元素级别的相乘,也就是两个相乘的数元素各自相乘,而不是矩阵乘法,注意和tf.matmul区别。
(2)两个相乘的数必须有相同的数据类型,不然就会报错。
2.tf.matmul()
将矩阵a乘以矩阵b,生成a * b。
格式: tf.matmul(a, b, transpose_a=False, transpose_b=False, adjoint_a=False, adjoint_b=False, a_is_sparse=False, b_is_sparse=False, name=None)
参数:
a: 一个类型为 float16, float32, float64, int32, complex64, complex128 且张量秩 > 1 的张量。
b: 一个类型跟张量a相同的张量。
transpose_a: 如果为真, a则在进行乘法计算前进行转置。
transpose_b: 如果为真, b则在进行乘法计算前进行转置。
adjoint_a: 如果为真, a则在进行乘法计算前进行共轭和转置。
adjoint_b: 如果为真, b则在进行乘法计算前进行共轭和转置。
a_is_sparse: 如果为真, a会被处理为稀疏矩阵。
b_is_sparse: 如果为真, b会被处理为稀疏矩阵。
name: 操作的名字(可选参数)
返回值: 一个跟张量a和张量b类型一样的张量且最内部矩阵是a和b中的相应矩阵的乘积。
注意:
(1)输入必须是矩阵(或者是张量秩 >2的张量,表示成批的矩阵),并且其在转置之后有相匹配的矩阵尺寸。
(2)两个矩阵必须都是同样的类型,支持的类型如下:float16, float32, float64, int32, complex64, complex12
tf.nn.dropout
tf.nn.dropout()是tensorflow里面为了防止或减轻过拟合而使用的函数,它一般用在全连接层
Dropout就是在不同的训练过程中随机扔掉一部分神经元。也就是让某个神经元的激活值以一定的概率p,让其停止工作,这次训练过程中不更新权值,也不参加神经网络的计算。但是它的权重得保留下来(只是暂时不更新而已),因为下次样本输入时它可能又得工作了
tf.nn.embedding_lookup
(
params,
ids,
partition_strategy='mod',
name=None,
validate_indices=True,
max_norm=None
)
参数说明:
params: 表示完整的嵌入张量,或者除了第一维度之外具有相同形状的P个张量的列表,表示经分割的嵌入张量
ids: 一个类型为int32或int64的Tensor,包含要在params中查找的id
partition_strategy: 指定分区策略的字符串,如果len(params)> 1,则相关。当前支持“div”和“mod”。 默认为“mod”
name: 操作名称(可选)
validate_indices: 是否验证收集索引
max_norm: 如果不是None,嵌入值将被l2归一化为max_norm的值
tf.nn.embedding_lookup()函数的用法主要是选取一个张量里面索引对应的元素
tf.nn.embedding_lookup(tensor,id):即tensor就是输入的张量,id 就是张量对应的索引
tf.negative()
取反的
理由有这样的需求 求两个tensor的相减的结果
tf.add(tensor1,tf.negtive(temsor2))
tf.reduce_sum
reduce_sum( ) 是求和函数,在 tensorflow 里面,计算的都是 tensor,可以通过调整 axis =0,1 的维度来控制求和维度。
python——random.sample()的用法
写脚本过程中用到了需要随机一段字符串的操作,查了一下资料,对于random.sample的用法,多用于截取列表的指定长度的随机数,但是不会改变列表本身的排序:
list = [0,1,2,3,4]
rs = random.sample(list, 2)
print(rs)
print(list)
》》》[2, 4] #此数组随着不同的执行,里面的元素随机,但都是两个
》》》[0, 1, 2, 3, 4]
上面这种方法要求知道已知的数列,但是不能满足我在一定范围内,随机出一定长度数据的要求。下面这种方法,跟range相结合,在指定范围内获取一定长度的数据,这个用起来就比较灵活,代码如下:
rs = random.sample(range(0, 9), 4)
print(rs)
》》》[2, 6, 0, 4]
这两个函数可以帮助我们在某个集合中找出最大或最小的N个元素。例如:
>>> import heapq
>>> nums=[1,8,2,23,7,-4,18,23,42,37,2]
>>> print(heapq.nlargest(3,nums))
>>> [42, 37, 23]
>>> print(heapq.nsmallest(3,nums))
>>> [-4, 1, 2]