推荐系统--矩阵分解(1)
推荐系统–矩阵分解(1)
推荐系统–矩阵分解(2)
推荐系统–矩阵分解(3)
推荐系统–矩阵分解(4)
推荐系统–矩阵分解(5)
推荐系统–矩阵分解(6)
1 引入
一个矩阵可以分解为两个小矩阵的乘积,以音乐为例,利用潜在特征向量来给用户和音乐打上标签:

以电影为例,利用潜在特征向量来给用户和电影打上标签:
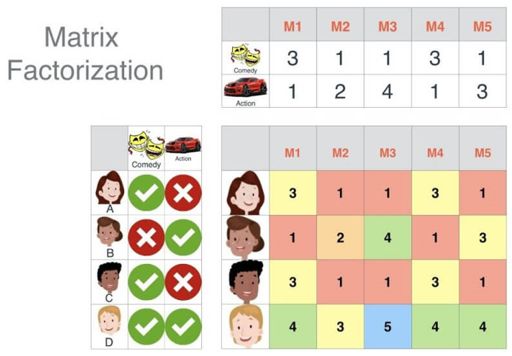
推荐系统的评分矩阵是稀疏的,这里的潜在特征不可解释,要模型自己去学, K K K代表潜在特征的维度,其大小决定决定了潜在特征的表达能力, K K K越大,信息表达就越强,即用户的兴趣和物品的分类划分得就越具体。
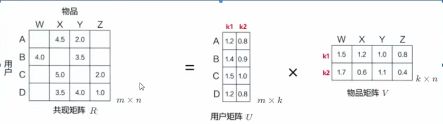
2 SVD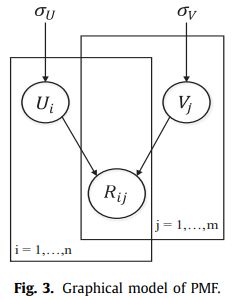
评分矩阵 R m × n R_{m \times n} Rm×n可以分解为两个小矩阵 U m × k U_{m \times k} Um×k, V n × k V_{n\times k} Vn×k;此处 k ≪ m & k ≪ n k \ll m \& k \ll n k≪m&k≪n。

U U U矩阵的一行表示用户 u u u的特征向量 p u p_u pu, V V V矩阵的一列表示物品 t i t_i ti的特征向量 q i q_i qi,利用这两个向量可以预测用户 u u u对物品 t i t_i ti的偏好:
Preference ( u , i ) = r u i ^ = p u T q i = ∑ k = 1 K p u , k q k , i (1) \operatorname{Preference}(u, i)=\hat{r_{u i}}=p_{u}^{T} q_{i}=\sum_{k=1}^{K} p_{u, k} q_{k, i} \tag1 Preference(u,i)=rui^=puTqi=k=1∑Kpu,kqk,i(1)
其优化目标函数为:
arg min θ L ( θ ) = 1 2 arg min ⏟ p u , q i ∑ u , i I u i [ ( r u i − p u T q i ) 2 ] + λ ( ∥ p u ∥ F 2 + ∥ q i ∥ F 2 ) (2) \argmin_{\theta} L(\theta)=\frac{1}{2}\underbrace{\arg \min }_{p_{u}, q_{i}} \sum_{u, i} I_{ui}\left[\left(r_{u i}-p_{u}^T q_{i}\right)^{2}\right] +\lambda(\|p_u\|_{F}^{2}+\|q_i\|_{F}^{2}) \tag2 θargminL(θ)=21pu,qi argminu,i∑Iui[(rui−puTqi)2]+λ(∥pu∥F2+∥qi∥F2)(2)
符号说明:
为了后面求梯度的时候好看一点,在函数前面加上了 1 2 \frac{1}{2} 21;
e u i = r u i − p u T q i e_{ui} = r_{u i}-p_{u}^T q_{i} eui=rui−puTqi;
θ \theta θ:矩阵分解的参数,即 p u , q i p_u, q_i pu,qi;
p u p_u pu:用户 u u u对应的向量,表示用户对电影某些题材的偏好程度,以潜在因子的方式表示;
q i q_i qi:项目 i i i对电影某些题材的符合程度,以潜在因子的方式表示;
λ \lambda λ:正则项的系数。
对公式(2)第一项求偏导,得到如下公式:
∂ L 1 ∂ p u , k = 1 2 ∂ ∂ p u , k ( e u i 2 ) = e u i ∂ ∂ p u , k e u i = e u i ∂ ∂ p u , k ( r u i − ∑ k = 1 K p u , k q k , i ) = − e u i q k , i ∂ L 1 ∂ q k , i = 1 2 ∂ ∂ p k , i ( e u i 2 ) = e u i ∂ ∂ p k , i e u i = e u i ∂ ∂ p k , i ( r u i − ∑ k − 1 K p u , k q k , i ) = − e u i p u , k \begin{aligned} \frac{\partial L_1}{\partial p_{u, k}} =\frac{1}{2}\frac{\partial}{\partial p_{u, k}}\left(e_{u i}^{2}\right)= e_{u i} \frac{\partial}{\partial p_{u, k}} e_{u i}=e_{u i} \frac{\partial}{\partial p_{u, k}}\left(r_{u i}-\sum_{k=1}^{K} p_{u, k} q_{k, i}\right)=-e_{u i} q_{k, i} \\ \frac{\partial L_1}{\partial q_{k, i}} =\frac{1}{2}\frac{\partial}{\partial p_{k, i}}\left(e_{u i}^{2}\right)= e_{u i} \frac{\partial}{\partial p_{k, i}} e_{u i}=e_{u i} \frac{\partial}{\partial p_{k, i}}\left(r_{u i}-\sum_{k-1}^{K} p_{u, k} q_{k, i}\right)=-e_{u i} p_{u, k} \end{aligned} ∂pu,k∂L1=21∂pu,k∂(eui2)=eui∂pu,k∂eui=eui∂pu,k∂(rui−k=1∑Kpu,kqk,i)=−euiqk,i∂qk,i∂L1=21∂pk,i∂(eui2)=eui∂pk,i∂eui=eui∂pk,i∂(rui−k−1∑Kpu,kqk,i)=−euipu,k
对公式(2)第二项求偏导,得到如下公式:
∂ L 2 ∂ p u , k = λ p u , k ∂ L 2 ∂ q k , i = λ q k , i \begin{aligned} \frac{\partial L_2}{\partial p_{u, k}} = \lambda p_{u, k} \\ \frac{\partial L_2}{\partial q_{k, i}} = \lambda q_{k, i} \end{aligned} ∂pu,k∂L2=λpu,k∂qk,i∂L2=λqk,i
整理后可得到迭代公式为:
p u , k = p u , k + η ( e u i q k , i − λ p u , k ) q k , i = q k , i + η ( e u i p u , k − λ q i , k ) (3) \begin{aligned} p_{u, k} &=p_{u, k}+\eta\left(e_{u i} q_{k, i}-\lambda p_{u, k}\right) \\ q_{k, i} &=q_{k, i}+\eta\left(e_{u i} p_{u, k}-\lambda q_{i, k}\right) \end{aligned} \tag3 pu,kqk,i=pu,k+η(euiqk,i−λpu,k)=qk,i+η(euipu,k−λqi,k)(3)
符号说明:
η \eta η: 更新步长,一般取0.005。