通过展开序列ISTA（SISTA）算法创建的递归神经网络（RNN）（Matlab代码实现）

      目录

1 概述

2 运行结果

3 参考文献

‍4 Matlab代码

---

1 概述

递归神经网络（recursive neural network）是具有树状阶层结构且网络节点按其连接顺序对输入信息进行递归的人工神经网络（Artificial Neural Network, ANN），是深度学习（deep learning）算法之一。

递归神经网络（recursive neural network）提出于1990年，被视为循环神经网络（recurrent neural network）的推广。当递归神经网络的每个父节点都仅与一个子节点连接时，其结构等价于全连接的循环神经网络。递归神经网络可以引入门控机制（gated mechanism）以学习长距离依赖。

递归神经网络具有可变的拓扑结构且权重共享，被用于包含结构关系的机器学习任务，在自然语言处理（Natural Language Processing, NLP）领域有受到关注。

本文包含通过展开序列ISTA（SISTA）算法创建的递归神经网络（RNN）的代码，用于序列稀疏编码。

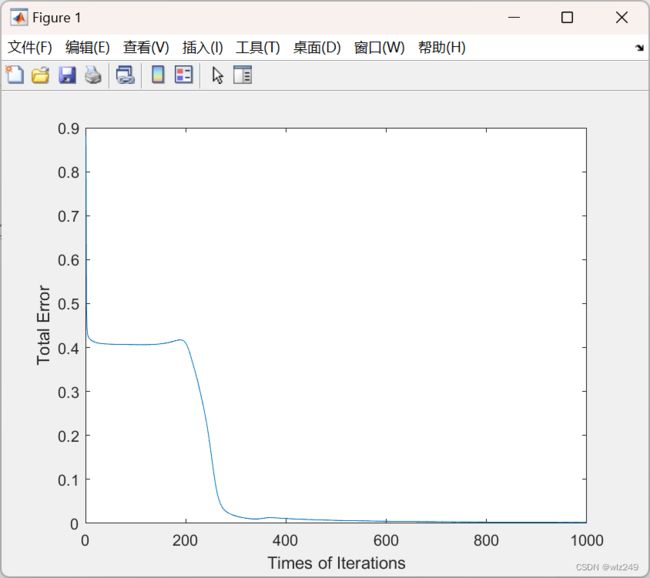
2 运行结果

 

 

 

3 参考文献

[1] S. Wisdom, T. Powers, J. Pitton, and L. Atlas, “Building Recurrent Networks by Unfolding Iterative Thresholding for Sequential Sparse Recovery,” ICASSP 2017, New Orleans, LA, USA, March 2017

[2] S. Wisdom, T. Powers, J. Pitton, and L. Atlas, “Interpretable Recurrent Neural Networks Using Sequential Sparse Recovery,” arXiv preprint arXiv:1611.07252, 2016. Presented at NIPS 2016 Workshop on Interpretable Machine Learning in Complex Systems, Barcelona, Spain, December 2016

‍4 Matlab代码

主函数部分代码：

for a = 1:4

    for b = 1:2
        W2(a, b) = rand();
    end

end

for v = 1:2

    for s = 1:4
        W1(v, s) = rand();
    end

end

% Training patterns
training_sets = [
        1, 0, 0, 0;
        0, 1, 0, 0;
        0, 0, 1, 0;
        0, 0, 0, 1];

% Initialise bias values
b1 = [rand(), rand()];
b2 = [rand(), rand(), rand(), rand()];

% Training iterations
for q = 1:1000

    % Total error
    Err = 0.0;

    % Training each pattern
    for z = 1:4

        % Calculate the output values of input layer
        for k = 1:4
            oi(k, 1) = 1 / (1 + exp(-training_sets(k, z)));
        end

        % Calculate the input values of hidden layer
        ih = W1 * oi + b1';

        % Calculate the output values of hidden layer
        for a = 1:2
            oh(a, 1) = 1 / (1 + exp(-ih(a)));
        end

        % Calculate the input values of output layer
        io = W2 * oh + b2';

        % Calculate the output values of output layer
        for b = 1:4
            oo(b, 1) = 1 / (1 + exp(-io(b)));
        end

        % ---- Total error of each pattern through the MLP ----
        Eot = 0.0;

        for b = 1:4
            Eo(b) = 1/2 * (training_sets(b, z) - oo(b, 1))^2;
            Eot = Eot + Eo(b);
        end