论文笔记Autoregressive Denoising Diffusion Models for Multivariate Probabilistic Time Series Forecasting
论文针对多元概率时间序列预测(multivariate probabilistic time series forecasting)任务,提出了TimeGrad模型。
有开源的代码:PytorchTS
概率预测如下图所示,对未来的预测带有概率:

TimeGrad模型基于Diffusion Probabilistic Model,Diffusion Probabilistic Model这里不再介绍,需要学习的请参见博客Denoising Diffusion Probabilistic Models简介
在了解Diffusion Probabilistic Model的基础上,这篇文章的方法非常简单。
方法
将多变量时间序列表示为 x i , t 0 ∈ R , i = { i , . . . , D } x_{i,t}^0\in \mathbb{R}, i=\{i,...,D\} xi,t0∈R,i={i,...,D},其中 t t t是时间index, D D D是多变量的变量数。给一个连续时间序列 t ∈ [ 1 , T ] t\in [1, T] t∈[1,T],将其划分为context window [ 1 , t 0 ) [1,t_0) [1,t0)和prediction window [ t 0 , T ] [t_0,T] [t0,T]。任务目的是用context window的时间序列预测prediction window的时间序列。
TimeGrad的是一个自回归(autoregressive)的模型:
q X ( x t 0 : T 0 ∣ x 1 : t 0 − 1 0 , c 1 : T ) = Π t = t 0 T q X ( x t 0 ∣ x 1 : t − 1 0 , c 1 : T ) (1) q_{\mathcal X}(\mathbf x_{t_0:T}^0 | \mathbf x_{1:t_0-1}^0, \mathbf c_{1:T})=\Pi_{t=t_0}^Tq_{\mathcal X}(\mathbf x_{t}^0 | \mathbf x_{1:t-1}^0, \mathbf c_{1:T}) \tag{1} qX(xt0:T0∣x1:t0−10,c1:T)=Πt=t0TqX(xt0∣x1:t−10,c1:T)(1)其中 c i , t \mathbf c_{i,t} ci,t是协变量(covariate),也就是特征,比如天气特征。
类似DeepAR,TimeGrad用RNN结构来建模历史的时间序列,得到隐状态(hidden state):
h t − 1 = RNN θ ( concat ( x t − 1 0 , c t ) , h t − 2 ) \mathbf h_{t-1}=\text{RNN}_\theta(\text{concat}(\mathbf x_{t-1}^0, \mathbf c_{t}), \mathbf h_{t-2}) ht−1=RNNθ(concat(xt−10,ct),ht−2)之后,再根据隐状态用Diffusion Probabilistic Model得到时间序列。
那么,公式(1)有近似:
Π t = t 0 T p θ ( x t 0 ∣ h t − 1 ) \Pi_{t=t_0}^T p_\theta(\mathbf x_{t}^0 | \mathbf h_{t-1}) Πt=t0Tpθ(xt0∣ht−1)这里的 θ \theta θ包含RNN的参数和Diffusion Probabilistic Model的参数。
训练时优化的损失是negative log-likelihodd:
∑ t = t 0 T − log p θ ( x t 0 ∣ h t − 1 ) \sum_{t=t_0}^T -\log p_\theta(\mathbf x_{t}^0 | \mathbf h_{t-1}) t=t0∑T−logpθ(xt0∣ht−1)
时间 t t t,噪声 n n n的diffusion model的优化目标是:
E x t 0 , ϵ , n ∥ ϵ − ϵ θ ( α ˉ t x 0 , ( 1 − α ˉ t ) ϵ , h t − 1 , n ) ∥ 2 \mathbb{E}_{\mathbf{x}_t^0,\epsilon,n}\|\epsilon-\epsilon_\theta(\sqrt{\bar{\alpha}_t}\mathbf{x}_0,\sqrt{(1-\bar{\alpha}_t)}\epsilon, \mathbf h_{t-1}, n)\|^2 Ext0,ϵ,n∥ϵ−ϵθ(αˉtx0,(1−αˉt)ϵ,ht−1,n)∥2其实就是Conditional Denoising Diffusion Probabilistic Models。
方法的结构图如下图所示。RNN产生每个时间点的隐状态,再用Diffusion Probabilistic Model由隐状态产生时间序列的值。因为RNN是自回归的,所以整个模型是自回归的。

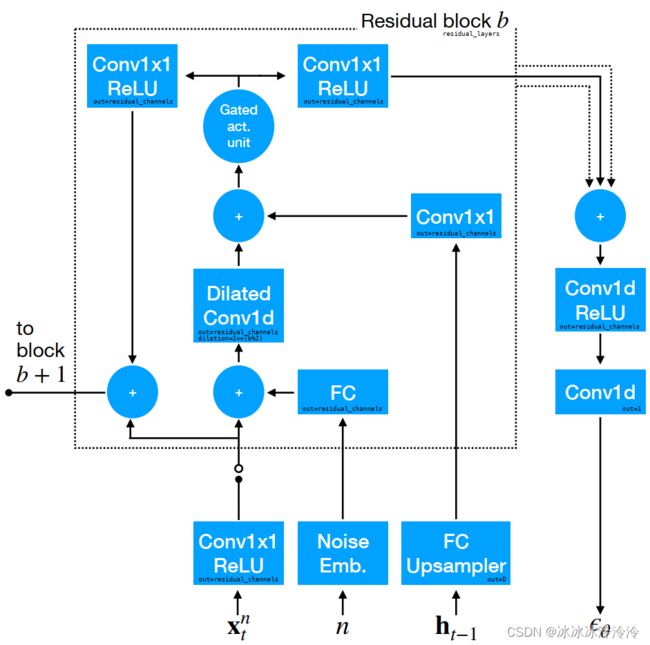
其中 ϵ θ \epsilon_\theta ϵθ的结构如下图:
评价指标
评价指标使用的是Continuous Ranked Probability Score (CRPS) 。
CRPS计算累计分布函数与观察值的兼容性。
CRPS ( F , x ) = ∫ R ( F ( z ) − I { x ≤ z } ) 2 d z \text{CRPS}(F, x) = \int_{\mathbb{R}}(F(z) - \mathbb I \{x \leq z \})^2 dz CRPS(F,x)=∫R(F(z)−I{x≤z})2dz在预测的分布和实际数据分布一致时,CRPS取得最小值。使用模型采样的样本可以近似计算预测的分布 F ^ ( z ) = 1 S ∑ s = 1 S I { x 0 , s ≤ z } \hat F(z)=\frac{1}{S} \sum_{s=1}^S \mathbb I \{x^{0,s} \leq z \} F^(z)=S1∑s=1SI{x0,s≤z}。
分别在时间序列的每一个维度计算CRPS。
另外,用 CRPS sum \text{CRPS}_{\text{sum}} CRPSsum表示时间序列所有维度的和。