机器学习-白板推导-系列（六）笔记：SVM

---

0 笔记说明

来源于【机器学习】【白板推导系列】【合集 1～23】，我在学习时会跟着up主一起在纸上推导，博客内容为对笔记的二次书面整理，根据自身学习需要，我可能会增加必要内容。

注意：本笔记主要是为了方便自己日后复习学习，而且确实是本人亲手一个字一个公式手打，如果遇到复杂公式，由于未学习LaTeX，我会上传手写图片代替（手机相机可能会拍的不太清楚，但是我会尽可能使内容完整可见），因此我将博客标记为【原创】，若您觉得不妥可以私信我，我会根据您的回复判断是否将博客设置为仅自己可见或其他，谢谢！

本博客为（系列六）的笔记，对应的视频是：【(系列六) 支持向量机1-硬间隔SVM-模型定义】、【(系列六) 支持向量机2-硬间隔SVM-模型求解-引出对偶问题】、【(系列六) 支持向量机3-硬间隔SVM-模型求解-引出KKT条件】、【(系列六) 支持向量机4-软间隔SVM-模型定义】、【(系列六) 支持向量机5-约束优化问题-弱队偶性证明】、【(系列六) 支持向量机6-约束优化问题-对偶关系之几何解释】、【(系列六) 支持向量机7-约束优化问题-对偶关系之Slater Condition】、【(系列六) 支持向量机8-约束优化问题-对偶关系之KKT条件】。

下面开始即为正文。

---

支持向量机（support vector machine，SVM）是一种二分类判别模型，分为三种：① 硬间隔（Hard Margin）SVM；② 软间隔（Soft Margin）SVM；③ Kernel SVM。

1 硬间隔SVM

数据集D中有N个样本实例，D = {(x₁, y₁), (x₂, y₂),…,(x_N, y_N)}，每个样本的x_i∈R^p，每个样本的y_i∈R，i=1…N，且y_i只取{+1,-1}中的一个值。

在下图中，假设x_i的维度为2，即x_i∈R²，超平面w^Tx+b将数据完全分为两类：o与×，但是这样的超平面不止一个。

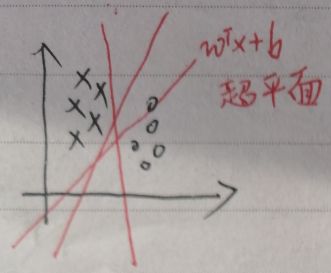
1.1 模型定义

SVM模型f(x)=sign(w^Tx+b)，sign(a)为符号函数，a≥0时为+1，a＜0为-1。硬间隔SVM又称为最大间隔分类器（最大间隔会在下面第一张图片提到）。首先定义任意一个样本(x_i, y_i)到超平面w^Tx+b的距离为distance(x_i,w,b)=|w^Tx_i+b|/||w||。针对任意一个样本(x_i, y_i)，因为f(x)=sign(w^Tx+b)，所以有【w^Tx_i+b>0时，y_i=+1】和【w^Tx_i+b<0时，y_i=-1】，注意到w^Tx_i+b与y_i总是同号，故综合而言有【y_i·(w^Tx_i+b)>0，i=1…N】。定义间隔Margin为N个样本到超平面w^Tx+b的距离中最小的那个距离，即Margin(w,b)为：

再整理一下：

1.2 对偶问题

原问题是带约束问题，由于有N个样本，所以有N个约束（上图最后一行），现在通过拉格朗日乘数法去寻找上述原问题的对偶无约束问题：

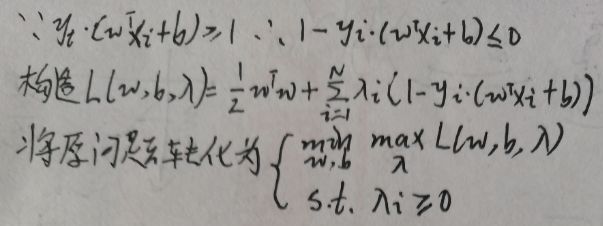
上图将带约束的原问题化为无约束问题（注意λ=(λ₁,λ₂,…,λ_N)），但是两个问题完全等价吗？下面进行验证：

根据上图，【1.1 模型定义】一节中最后一张图片定义的原问题与本节【1.2 对偶问题】中第一张图片最后两行的问题完全等价。

根据【3.1 弱对偶性证明】一节的内容，本问题中可以将【min max】换为【max min】，即问题变为：

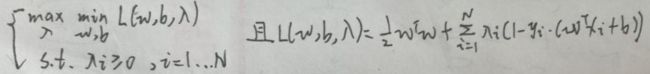
下面进行求解：

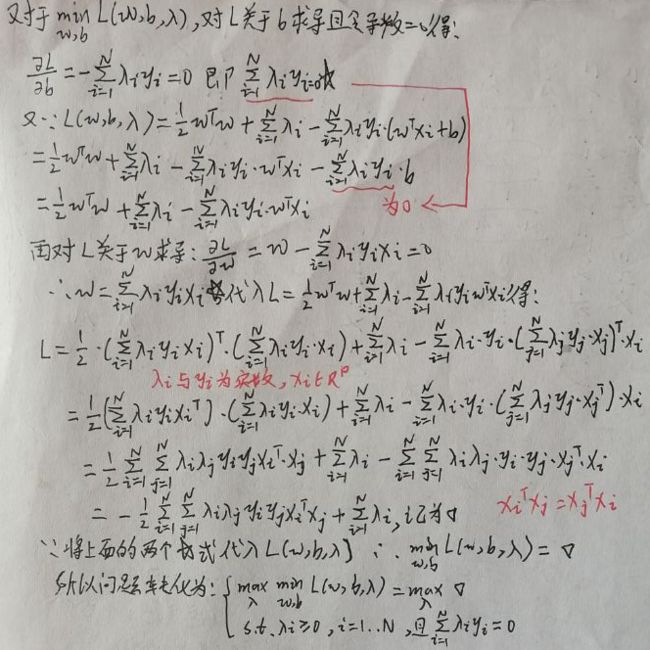
1.3 KKT条件

为方便，先将max问题化为min问题：

因为【1.1 模型定义】一节中最后一张图片定义的原问题与【1.2 对偶问题】一节中第一张图片最后两行的问题完全等价，而上图的问题（记为问题#）与上述两个问题等价，所以原问题与问题#完全等价，问题#称为原问题的对偶问题，且问题#与原问题具有强对偶关系，所以满足KKT条件（我并不明白）如下：

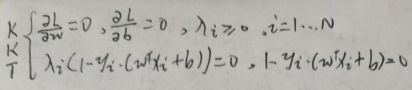
在下图中，假设x_i的维度为2，即x_i∈R²。设【当w^Tx_i+b≥+1时，y_i=+1】和【当w^Tx_i+b≤-1时，y_i=-1】。图中已标出最佳的超平面w^Tx+b，并且，在另外两个平面即w^Tx+b=±1上的那些样本点(x_k, y_k)就称作支持向量（support vector）。

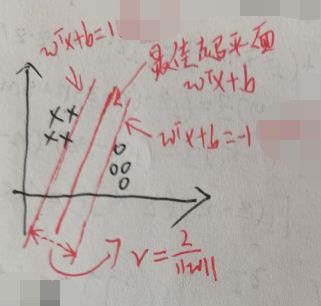
在两个平面即w^Tx+b=±1上的支持向量到超平面w^Tx+b的距离相同，距离之和为r=2/||w||。

现在求解w与b。根据【1.2 对偶问题】一节中最后一张图片的中间某行（自己去看）可得：

现在求解b。因为任意一个支持向量(x_k, y_k)均在两个平面即w^Tx+b=±1之一上，且y_k只取{+1,-1}中的一个值，i=1…N，所以有【y_k=+1时，支持向量(x_k, y_k)在平面w^Tx+b=+1上】和【y_k=-1时，支持向量(x_k, y_k)在平面w^Tx+b=-1上】，则对于所有支持向量(x_k, y_k)，有y_k·(w^Tx_k+b)=1。同左乘y_k得：y_k²·(w^Tx_k+b)=y_k，因为y_k只取{+1,-1}中的一个值，所以y_k²=1，所以w^Tx_k+b=y_k，所以b=y_k-w^Tx_k：

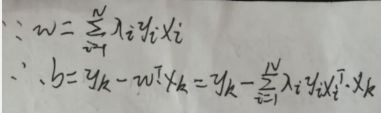
理论上，可选取任意支持向量(x_k, y_k)，并通过上图的公式获得b，但更常采用一种更鲁棒的做法是使用所有支持向量求解的平均值作为b（下图的|S|为集合S的元素总个数）：

1.4 最终模型

最终模型为f(x)=sign(w^Tx+b)，超平面为w^Tx+b，其中w与b为：

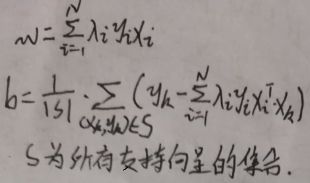
上图中λ_i≥0。由【1.3 KKT条件】一节中的第二张图片的KKT条件，有：λ_i(1-y_i·(w^Tx_i+b))=0，且1-y_i·(w^Tx_i+b)≤0。因此对于任意一个样本(x_i, y_i)，有两种情况：

（1）1-y_i·(w^Tx_i+b)<0，即不在两个平面即w^Tx+b=±1之一上的样本，此时λ_i=0，即这些样本不参与计算w和b（在公式中如果λ_i=0，肯定就不参与计算咯，自己去看公式就懂了）；

（2）1-y_i·(w^Tx_i+b)=0，即所有支持向量，此时λ_i>0。这表明了SVM在训练完成后，大部分的训练样本都不需要保留，最终模型仅与支持向量有关。

---

2 软间隔SVM

相比于硬间隔SVM，软间隔SVM允许一定的错误。先复习下硬间隔SVM的原问题：

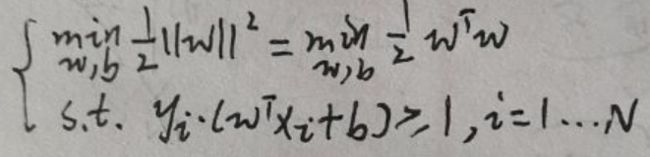
软间隔在最优化问题中加入了loss，先看下面的loss：

根据上图右下角的图像，显然上述loss是不连续的。下面是一个连续的loss：

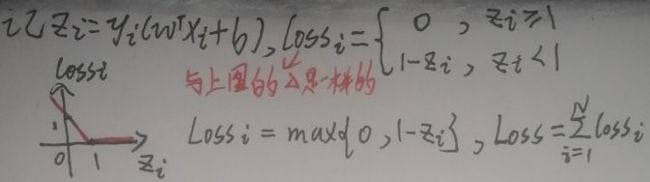
根据上图左下角的图像，显然上述loss是连续的。因此软间隔SVM的模型（c为超参数）为：

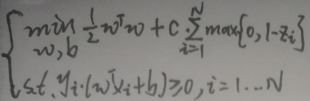
不知道为啥，软间隔SVM引入了一个ξ_i=1-y_i·(w^Tx_i+b))，ξ_i≥0，所以软间隔SVM的最终模型为：

up主未详细求解模型参数，我也就偷懒不弄了，以后用到可能会补充。

---

3 约束优化问题

3.1 弱对偶性证明

本节是对原问题和其对应的对偶问题的弱对偶性证明。假设下面为原问题：

引入拉格朗日函数（注意是η而不是y哦）：

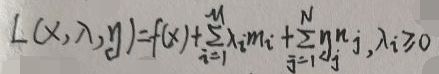
则原问题变为：

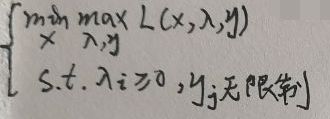
下面证明原问题与加入拉格朗日函数的原问题（记为L问题）是等价的，即证明本节第一、三张图片的问题是等价的。

首先二者均是求关于x的最小值，这一点相同。

考虑两种情况：① 若L问题中的x违反了原问题的不等式约束m_i(x)≤0，即在L问题中m_i(x)＞0，通过观察L(x,λ,η)，λ_i≥0，则λ_i·m_i≥0，若求max L(x,λ,η)，max(λ_i·m_i)显然为+∞，即无最大值；② 若L问题中的x符合原问题的不等式约束m_i(x)≤0，若求max L(x,λ,η)，由于λ_i≥0，max(λ_i·m_i)显然不是+∞（非负数与非正数相乘最大值为0，此时λ_i或m_i取0），即此时最大值max L(x,λ,η)存在。综合两种情况：

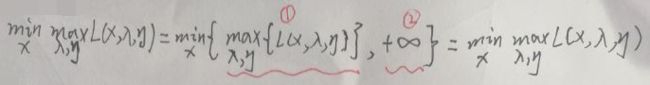
注意上面的两部分①和②分别就是上述两种情况的结果，最终的值只取了①——这意味着L问题本身就蕴含了原问题中的不等式约束m_i(x)≤0，将m_i(x)＞0给“过滤了，不再考虑了”。因此L问题与原问题是完全等价的。于是现在将L问题称为原问题，即原问题如下：

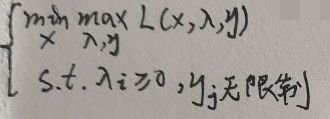
原问题的对偶问题为：

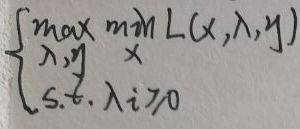
注意：① 原问题是关于x求最小值的问题；② 对偶问题为关于λ、η求最大值的问题。下面证明二者之间的弱对偶性：

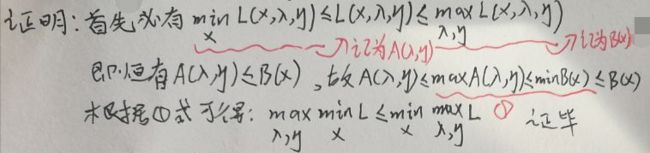
因此原问题与对偶问题具有弱对偶性。

3.2 对偶关系之几何解释

现在解释【3.1 弱对偶性证明】一节第一张图片定义的原问题的几何意义。为了便于解释，去掉等式约束，且假设只有一个不等式约束，假设f(x)是可微的（在【3.4 对偶关系之KKT条件】一节的梯度为0会再次提到可微，现在不懂没事，后面会再说一次），即原问题变为：

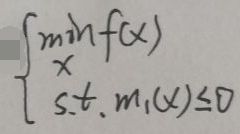
上述问题的x∈R^p，即x是p维向量；f(x)的定义域设为domain f，m₁(x)的定义域为domain m₁，则原问题定义域为【D=domain f ∩ domain m₁】，即二者的交集，下面引入拉格朗日函数：

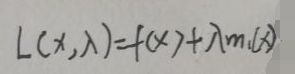
注意λ≥0。引入拉格朗日函数后原问题变为：

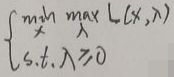
现在记上面的问题为原问题，其对偶问题为：

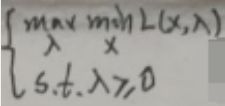
构造区域G={(m₁(x),f(x))|x∈D}，显然G为一个点集，且为二维坐标系的一个区域，现在假设p^*和d^*分别为原问题、对偶问题的最优解，即：

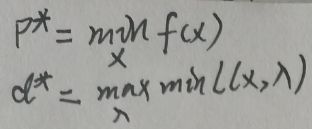
为后续书写方便，现在记u=m₁(x)，t=f(x)，于是G={(u,t)|u=m₁(x),t=f(x),x∈D}，以横纵坐标轴分别为u、t，表示区域G为：

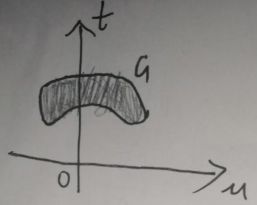
G为图中阴影部分。此时p^*和d^*分别变为：

为了明确p^*和d^*中的g(λ)，再写一次：

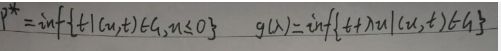
注意inf表示集合的下确界。现在怎么在图中表示p^*和g(λ)呢？先看p^*：首先纵轴t将G分为左右两部分，而【(u,t)∈G,u≤0】表示G的左半部分，因此集合{t|(u,t)∈G,u≤0}就是将G的左半部分所有点投影在t轴上，如下图：

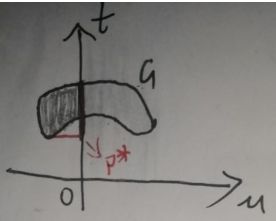
{t|(u,t)∈G,u≤0}就是上图纵轴t加粗的那部分了，因此p^*=inf{t|(u,t)∈G,u≤0}就是加粗部分的最下面最小的那个值，已经在图上标出了。

现在再看g(λ)=inf{t+λu|(u,t)∈G}：先暂时令t+λu=0，记t=-λu，由于λ＞0，所以t=-λu在上图的坐标轴中就是一条过原点、斜率为-λ的一条像汉字中的“㇏”（即捺）一样的直线。现在令t+λu=Δ，即t=Δ-λu，则在坐标轴中就是过点(0,Δ)、斜率为-λ的一条直线，如下图：

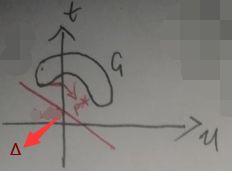
这条直线与纵轴t的交点的纵坐标的大小就是Δ。{t+λu|(u,t)∈G}便是【不断平移直线t=Δ-λu，使直线与区域G有交点，这样得到的所有直线与纵轴t的交点的纵坐标的大小Δ_i构成的集合】。所以g(λ)=inf{t+λu|(u,t)∈G}是取上述集合即Δ_i中最小的那个，比如说记为Δ₁，如下图：

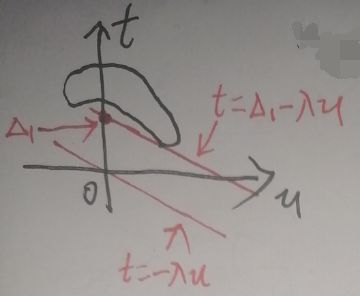
即g(λ)=Δ₁，而d^*为：

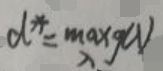
而p^*和d^*分别为原问题、对偶问题的最优解，又因为原问题与对偶问题具有弱对偶性，根据【3.1 弱对偶性证明】一节最后一张图片中的不等式关系有：d^*=max g(λ)=max Δ₁≤p^*。若区域G为凸的，如下：

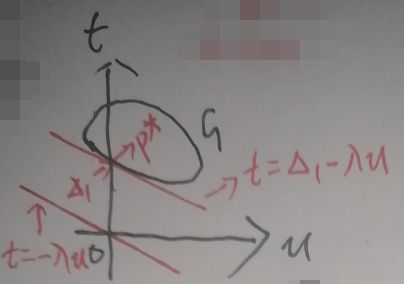
上图中d^*=Δ₁=p^*，当然我是故意这么画的。

事实上，若【原问题为凸优化问题，且满足slater条件】，则一定有【d^*=p^*】。注意前者是后者的充分非必要条件（我并不懂）。而本篇博文的主题SVM本身就是凸二次规划问题，凸二次规划问题一定满足slater条件，所以SVM一定有d^*=p^*，即原问题与对偶问题具有强对偶性。

3.3 对偶关系之slater条件

slater条件是这样的：

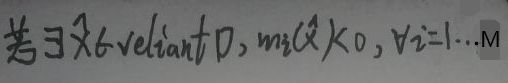
relian D是“相对内部”，它是这样的：若区域D有边界，则relian D为去掉边界的D；若区域D无边界，则relian D=D。举个栗子，若D为圆，则去掉圆环的圆面就是relian D。

对于多数凸优化问题，slater条件一定成立。也就是说存在某些凸优化问题不满足slater条件，下面介绍“放松的slater条件”：若M个不等式约束中有K个m_i(x)是仿射函数，仿射函数就是最高次数为1的多项式函数，则只需校验剩下的M-K个约束。

对于原问题：

在凸二次规划问题中的f(x)是凸函数（凸函数是定义在某个向量空间的凸子集C上的实值函数），且m_i(x)与n_j(x)均是仿射函数，即凸二次规划问题满足“放松的slater条件”。

“放松的slater条件”是对区域G做出了限制，为了便于解释，现在考虑只有一个不等式约束，如u=m₁(x)≤0，如下图：

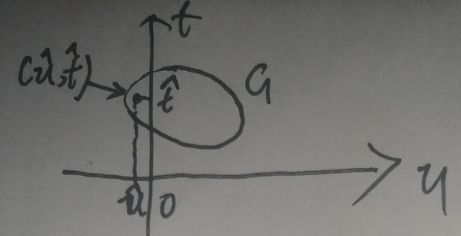
“放松的slater条件”限制G中必须至少存在一个点在纵轴t的左面。这样的限制使得直线t=Δ-λu一定不会垂直于横轴u。

总之，若原问题中f(x)是凸函数，且原问题满足slater条件，则一定有d^*=p^*，即原问题与对偶问题具有强对偶性。

3.4 对偶关系之KKT条件

p^*和d^*分别为原问题、对偶问题的最优解，而原问题、对偶问题分别是关于x、λ和η的函数，因此可分别为记p^*为x^*、记d^*为λ^*和η^*。

KKT条件给出了判断x^*是否为最优解的必要条件，KKT条件可分为三部分：① 可行条件；② 互补松弛条件；③ 梯度为0。

3.4.1 可行条件

根据【3.1 弱对偶性证明】一节中第一张、倒数第二张图片中定义的原问题与对偶问题，代入最优解x^*、λ^*可得：

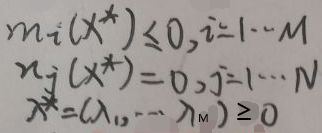
上图即为可行条件。

3.4.2 互补松弛条件

看下图：

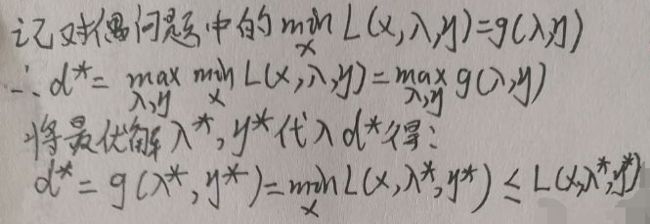
因为图片最后一行对任意x都成立，所以可将x^*代入得：

最后一行即为互补松弛条件（右上角纸张有点扭曲，并没有内容）。

3.4.3 梯度为0

---

4 Kernel SVM

先看【1.3 KKT条件】一节中第一张图片，即：

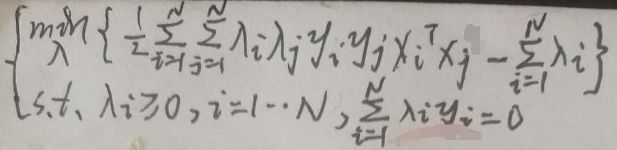
如果SVM解决的是非线性可分问题，可以利用核函数（请看此博文）将低维非线性可分问题转换为高维线性可分问题——将上图的x_i^Tx_j=i,x_j>换为<φ(x_i),φ(x_j)>=φ(x_i)^Tφ(x_j)，然后再按照顺序求解即可。

这样的模型就叫做Kernel SVM。

---

END