人工智能：用遗传算法近似求解TSP问题（附有实验报告资源和Python源代码）

项目简介

这是人工智能实验课的一次作业。项目文件有两个py文件，其中Main.py文件中是算法的主体，而一些具体的步骤实现则放在AidFunctions.py文件中。代码注释比较详细，可以对照实验报告进行阅览。

项目代码

Main.py

import numpy as np
import AidFunctions
import matplotlib.pyplot as plt
import random
import time

#### 参数定义区域 ####
CityCount=100           # 定义城市个数
GroupCount=50         # 定义群体中的个体数
MaxIteration=100       # 定义最大迭代次数
SelectFactor=0.1       # 定义选择概率算子
CrossFactor=0.2       # 定义交叉概率算子
VariationFactor=0.05   # 定义变异概率算子

#### 其他变量定义区域 ####
np.random.seed(1) # 固定Numpy随机数种子
random.seed(1)    # 固定随机数种子
timeGap=0         # 记录程序的执行时间（不包括作图部分）

#### 主函数部分 ####

# 首先通过随机数生成指定个数城市的横纵坐标（此时不考虑三维情况）
X = np.random.uniform(1, 100, (1, CityCount))
Y = np.random.uniform(1, 100, (1, CityCount))
# 根据城市个数生成城市距离矩阵
DistanceMatrix=AidFunctions.GetDistanceMatrix(X,Y,CityCount)
# 根据群体中的个体个数通过随机的方法生成初始群体
Group=[]
for i in range(GroupCount):
    Primary_Individual=np.arange(CityCount)
    np.random.shuffle(Primary_Individual)
    Group.append(Primary_Individual)

# 开始进行计时
start=time.time()

# 在最大迭代次数内，重复执行适应度计算、选择、交叉和变异过程

# 首先定义一些运算过程中所需要使用到的参数
SelectCount=int(SelectFactor*GroupCount)        # 选择个数参数，需要从浮点型转换为整数类型
CrossCount=int(CrossFactor*GroupCount)          # 交叉个数参数，需要从浮点型转换为整数类型
VariationCount=int(VariationFactor*GroupCount) # 变异个体参数，需要从浮点型转换为整数类型
Average_Distance=[]                       # 记录每一次迭代后种群中个体的平均距离
Max_Distance=[]                           # 记录每一次迭代后种群中个体的最大距离
Min_Distance=[]                           # 记录每一次迭代后种群中个体的最小距离
Max_Pos=-1                                # 记录当前最长距离所对应的路线在群体中的位置
Min_Pos=-1                                # 记录当前最段距离所对应的路线在群体中的位置
# 正式的运算部分
for i in range(MaxIteration):
    # 获取当前群体各自的总距离（总距离可以视为适应度函数的互补函数）
    TotalDistanceArray=AidFunctions.GetTotalDistances(DistanceMatrix,Group)

    Average_Distance.append(np.average(TotalDistanceArray))
    Max_Distance.append(np.max(TotalDistanceArray))
    Min_Distance.append(np.min(TotalDistanceArray))
    Max_Pos=np.argmax(TotalDistanceArray)
    Min_Pos=np.argmin(TotalDistanceArray)

    # 接下来进行选择操作：进行选择时可以使用下面三种方法中的任意一种
    # 第一种选择方法：根据选择概率因子来用适应度最高的一些个体替换等数量的适应度最低的个体来实现选择的目的
    #Group=AidFunctions.SelectAndReplace(TotalDistanceArray,SelectCount,Group)
    # 第二种选择方法：适应度比例方法
    Group=AidFunctions.MonteCarlo(TotalDistanceArray,Group,GroupCount)
    # 第三种选择方法：线性排序方法
    #Group=AidFunctions.LinerSort(TotalDistanceArray,Group,GroupCount)

    # 接下来进行交叉互换操作：每一次互换一个基因，基因的位置由随机数确定
    Group=AidFunctions.Cross(Group,CrossCount,CityCount)

    # 接下来进行变异操作：变异过程为交换基因上的随机两点
    # 第一种变异方式：个体的随机两个基因位置发生交换
    Group=AidFunctions.SwapRandomTwoGenes(Group,CityCount,GroupCount,VariationCount)
    # 第二种变异方式：个体的相邻两个基因位置发生交换
    #Group=AidFunctions.SwapNearbyTwoGenes(Group,CityCount,GroupCount,VariationCount)

# 画图前停止计时
end=time.time()
timeGap=end-start

# 绘制种群个体的平均总距离随迭代次数的变化曲线
plt.figure(2)
Average_Line,=plt.plot(range(1,MaxIteration+1),Average_Distance,'r-')
Max_Line,=plt.plot(range(1,MaxIteration+1),Max_Distance,'g-')
Min_Line,=plt.plot(range(1,MaxIteration+1),Min_Distance,'b-')
plt.legend([Average_Line,Max_Line,Min_Line],["Average","Max","Min"],loc='upper right')
plt.xlabel("迭代次数",fontproperties="Simhei")
plt.ylabel("距离",fontproperties="Simhei")
plt.title("距离随迭代次数变化情况图",fontproperties="Simhei")
plt.grid(True)
plt.show()

## 绘制最长和最短距离的路线 ##
# 首先进行一些数据准备
MinRoute=Group[Min_Pos].tolist()
MinRoute_X=[]
MinRoute_Y=[]
# 由于Numpy的ndarray类型不方便后续操作，因此首先将其转换为列表类型
X=X[0,:].tolist()
Y=Y[0,:].tolist()
for i in range(CityCount):
    MinRoute_X.append(X[MinRoute[i]])
    MinRoute_Y.append(Y[MinRoute[i]])
MinRoute_X.append(MinRoute_X[0])
MinRoute_Y.append(MinRoute_Y[0])
plt.figure(3)
PointsLine,=plt.plot(X,Y,'r''o')
MinRouteLine,=plt.plot(MinRoute_X,MinRoute_Y,'b-')
plt.xlabel("横坐标",fontproperties="Simhei")
plt.ylabel("纵坐标",fontproperties="Simhei")
plt.title("最短路径展示图",fontproperties="Simhei")
plt.legend([PointsLine,MinRouteLine],["City","ShortestPath"])
plt.show()

# 通过控制台输出程序的运行结果
print("最终的最短路径长度为："+str(Min_Distance[MaxIteration-1])+"km")
print("最终种群的平均适应度为："+str(10000/Average_Distance[MaxIteration-1]))
print("最终种群的最高适应度为："+str(10000/Min_Distance[MaxIteration-1]))
print("最终种群的最低适应度为："+str(10000/Max_Distance[MaxIteration-1]))
print("程序的执行时间为："+str(timeGap)+"s")

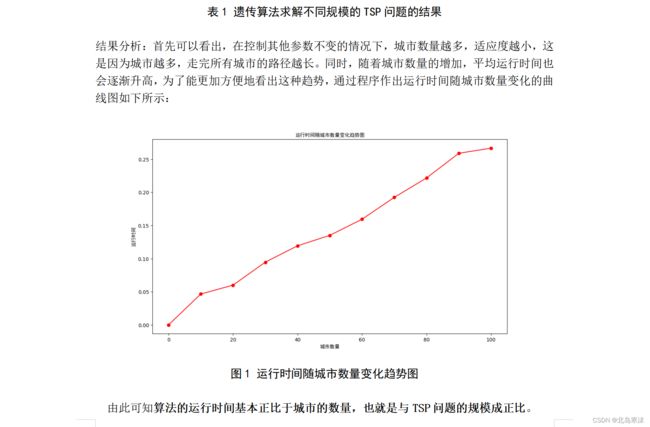
# 取整十数个城市进行测试，作出运行时间和城市个数（TSP问题规模）之间的关系图
plt.figure(4)
plt.plot([0,10,20,30,40,50,60,70,80,90,100],[0,0.046599,0.060017,0.094630,0.119404,0.135133,0.159484,0.192489,0.221779,0.259008,0.266784],'r-o')
plt.xlabel("城市数量",fontproperties="Simhei")
plt.ylabel("运行时间",fontproperties="Simhei")
plt.title("运行时间随城市数量变化趋势图",fontproperties="Simhei")
plt.show()

AidFunctions.py

import numpy as np
import matplotlib.pyplot as plt
import random
import heapq

####求出距离矩阵的函数 ####
def GetDistanceMatrix(X,Y,CityCount):
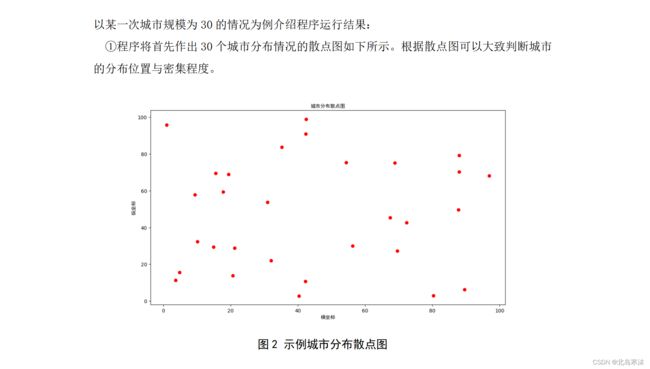
    # 作出初始城市位置的散点图
    plt.figure(1)
    plt.plot(X,Y,'r''o')
    plt.xlabel("横坐标",fontproperties="Simhei")
    plt.ylabel("纵坐标",fontproperties="Simhei")
    plt.title("城市分布散点图",fontproperties="Simhei")
    plt.show()
    # 生成一个方阵作为任意两城市之间的距离矩阵
    DistanceMatrix=np.zeros((CityCount,CityCount))
    # 通过逐行逐列遍历的方式填充矩阵元素（第i行第j列的元素表示i和j两个城市之间的距离）
    for row in range(CityCount):
        for col in range(CityCount):
            DistanceMatrix[row,col]=((X[0,row]-X[0,col])**2+(Y[0,row]-Y[0,col])**2)**0.5
    # 将进行了填充后的距离矩阵返回输出
    return DistanceMatrix

#### 求某一代群体每个个体各自的总距离的函数 ####
def GetTotalDistances(DistanceMatrix,Group):
    # 定义用于记录每一个个体的总距离的向量
    DistancesVector=np.zeros((1,len(Group)))
    # 使用循环的方式分别计算每一个个体的总距离
    for individual in range(len(Group)):
        for i in range(1,Group[individual].size):
            DistancesVector[0,individual]+=DistanceMatrix[Group[individual][i-1],Group[individual][i]]
    return DistancesVector

#### 直接进行精英替换的的选择操作的函数 ####
def SelectAndReplace(TotalDistanceArray,SelectCount,Group):
    # 首先定义一个数组用于表示某一个个体是否被选出来进行替换或被替换
    Selected=np.zeros((1,TotalDistanceArray.size))
    # 从适应度最高的个体开始进行逐一替换
    for i in range(SelectCount):
        # 用两个变量分别记录某一次遍历中的最大值和最小值，同时用另外两个变量记录局部最大值和最小值的下标
        CurrentMax=0
        CurrentMin=99999999
        maxPos=-1
        minPos=-1
        for individual in range(len(Group)):
            if(TotalDistanceArray[0,individual]>CurrentMax and Selected[0,individual]==0):
                CurrentMax=TotalDistanceArray[0,individual]
                maxPos=individual
            if(TotalDistanceArray[0,individual]<CurrentMin and Selected[0,individual]==0):
                CurrentMin=TotalDistanceArray[0,individual]
                minPos=individual
        # 记录已经被选择过的位置
        Selected[0,maxPos]=1
        Selected[0,minPos]=1
        # 将最大值位置的个体更换为小大值位置的个体
        Group[maxPos]=Group[minPos]
        return Group

#### 使用适应度比例方法的选择函数 ####
def MonteCarlo(TotalDistanceArray,Group,GroupCount):
    # 首先由于计算出的总距离的都是正数，因此可以用其倒数作为适应度函数，由此按照每个个体的总距离求出每个个体的适应度
    FitnessVector=1/TotalDistanceArray[0,:]
    # 按照适应度比例方法的原理，以适应度的比例作为抽取概率
    ProbilityVector=FitnessVector/sum(FitnessVector)
    # 将抽取结果暂时存放在ChoiceList变量中，之后根据记录的结果逐一向新群体中添加个体
    temp=np.arange(GroupCount)
    ChoiceList=(np.random.choice(temp,(1,GroupCount),replace=True,p=ProbilityVector))[0,:].tolist()
    NewGroup=[]
    for i in range(GroupCount):
        NewGroup.append(Group[ChoiceList[i]])
    # 最终修改原始群体
    return NewGroup

#### 使用线性排序方法的选择函数 ####
def LinerSort(TotalDistanceArray,Group,GroupCount):
    # 首先定义一个可能性向量用于存放抽取概率
    ProbilityVector=np.full((1,GroupCount),GroupCount)[0,:].tolist()
    # 求出每个元素的大小顺序，并将结果进行保存
    index=list(map(TotalDistanceArray[0,:].tolist().index,heapq.nlargest(GroupCount,TotalDistanceArray[0,:].tolist())))
    for i in range(GroupCount):
        ProbilityVector[i]-=index[i]
    # 求出最终的概率向量
    ProbilityVector=(np.array(ProbilityVector)/np.sum(ProbilityVector).tolist())
    # 将抽取结果暂时存放在ChoiceList变量中，之后根据记录的结果逐一向新群体中添加个体
    temp=np.arange(GroupCount)
    ChoiceList=(np.random.choice(temp,(1,GroupCount),replace=True,p=ProbilityVector))
    NewGroup=[]
    for i in range(GroupCount):
        NewGroup.append(Group[ChoiceList[0,i]])
    # 最终修改原始群体
    return NewGroup


#### 进行交叉互换的函数 ####
def Cross(Group,CrossCount,CityCount):
    # 如果交叉互换的个体数不是偶数，则将其变为偶数
    if(CrossCount//2==1):
        CrossCount+=1
    # 逐对进行交叉互换
    for couple in range(CrossCount//2):
        # 每次随机从当前群体中找出两个个体进行交叉互换
        Individual1 = Group[random.randint(0,len(Group))-1]
        Individual2 = Group[random.randint(0,len(Group))-1]
        # 通过随机数确定发生交换的基因位置
        pos=random.randint(0,CityCount-1)
        # 记录需要交换的基因和相应的位置
        gene1=Individual1[pos]
        gene2=Individual2[pos]
        index1=Individual1.tolist().index(gene2)
        index2=Individual2.tolist().index(gene1)
        # 交换两组基因
        Individual1[pos]=gene2
        Individual2[pos]=gene1
        Individual1[index1]=gene1
        Individual2[index2]=gene2
    # 返回经过交叉互换后的种群
    return Group

#### 进行随机两点交换的变异函数 ####
def SwapRandomTwoGenes(Group,CityCount,GroupCount,VariationCount):
    # 按照变异个体数，每一次随机取出一个个体进行变异
    for count in range(VariationCount):
        Individual=random.randint(0,GroupCount-1)
        # 随机确认两个发生变异的基因
        pos1=random.randint(0,CityCount-1)
        pos2=random.randint(0,CityCount-1)
        # 获取这两个位置上的基因
        gene1=Group[Individual][pos1]
        gene2=Group[Individual][pos2]
        # 交换这两个基因
        Group[Individual][pos1]=gene1
        Group[Individual][pos2]=gene2
    return Group

#### 进行相邻两点交换的变异函数 ####
def SwapNearbyTwoGenes(Group,CityCount,GroupCount,VariationCount):
    # 按照变异个体数，每一次随机取出一个个体进行变异
    for count in range(VariationCount):
        Individual=random.randint(0,GroupCount-1)
        # 确定随机发生相邻交换变异的基因位置
        pos=random.randint(1,CityCount-1)
        # 获取相邻两个位置上的基因
        gene1=Group[Individual][pos-1]
        gene2=Group[Individual][pos]
        # 交换这两个基因
        Group[Individual][pos-1]=gene2
        Group[Individual][pos]=gene1
    return Group

实验报告

实验报告部分内容如下图所示：

实验报告资源获取 提取码：8cr0